C++使用数组来实现哈夫曼树

目录
  • 写在前面
  • 构造思想
  • 算法设计
  • 构造实例
  • 理解代码
    • 确定结构体
    • 循环找出最小值
    • 调用细节
    • 调试试图
  • 总结

写在前面

哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1*L1+W2*L2+W3*L3+...+Wn*Ln），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。可以证明霍夫曼树的WPL是最小的；但是今天，咱们不谈哈夫曼编码，就只用结构体配合数组来完成哈夫曼树的生成，目标是得到正确的所有权值的和。

构造思想

以字符的使用频率做权构建一棵哈夫曼树，然后利用哈夫曼树对字符进行编码，俗称哈夫曼编码。具体来讲，是将所要编码的字符作为叶子结点，该字符在文件中的使用频率作为叶子结点的权值，以自底向上的方式、通过执行n-1次的“合并”运算后构造出最终所要求的树，即哈夫曼树，它的核心思想是让权值大的叶子离根最近。每次从树的集合中取出双亲为0且权值最小的两棵树作为左、右子树，构造一棵新树，新树根结点的权值为其左右孩子结点权之和，将新树插入到树的集合中。

算法设计

步骤1：确定合适的数据结构。

步骤2：初始化。构造n棵结点为n个字符的单结点树集合F={T1，T2,…, Tn}，每棵树中只有一个带权的根结点，权值为该字符的使用频率；

步骤3：如果F中只剩下一棵树，则哈夫曼树构造成功，转步骤6；否则，从集合F中取出双亲为0且权值最小的两棵树Ti和Tj，将它们合并成一棵新树Zk，新树以Ti为左儿子， Tj为右儿子（反之也可以）。新树Zk的根结点的权值为Ti与Tj的权值之和；

步骤4：从集合F中删去Ti、Tj，加入Zk；

步骤5：重复步骤3和4；

步骤6：从叶子结点到根结点逆向求出每个字符的哈夫曼编码（约定左分支表示字符“0”，右分支表示字符“1”）。则从根结点到叶子结点路径上的分支字符组成的字符串即为叶子字符的哈夫曼编码。算法结束。

构造实例

已知某系统在通信联络中只可能出现8种字符，分别为a，b，c，d，e，f，g，h，其使用频率分别为0.05，0.29，0.07，0.08，0.14，0.23，0.03，0.11，试设计哈夫曼编码。设权w=(5，29，7，8，14，23，3，11)，n=8，按哈夫曼算法的设计步骤构造一棵哈夫曼编码树，具体过程如下：

理解代码

源码：

#include <iostream>
using namespace std;
#define N 8
struct Node
{
	char L;//字母
	int K;//权值
	bool IsRoot;//是否为根结点
	int Lc, Rc;//左右子树
	Node(char l = '/0', int k = 0, bool isRoot = false) {
		L = l; K = k; IsRoot = isRoot; Lc = Rc = -1;
	}
};
Node A[N + N - 1] = { Node('a',5,true) , Node('b',29,true), Node('c',7,true), Node('d',8,true),
				      Node('e',14,true), Node('f',23,true), Node('g',3,true), Node('h',11,true) };
void FindMin(Node A[], int &min1, int &min2,int num)
{
	min1 = num - 1;
	for (int i = 0; i < num; i++) {
		if (A[i].IsRoot && A[i].K < A[min1].K) min1 = i;
	}
	min2 = num - 1;
	for (int i = 0; i < num; i++) {
		if (min1 != i && A[i].IsRoot &&A[i].K < A[min2].K) min2 = i;
	}
}
int main()
{
	int y = 1, num = N;
	int min1=0, min2=0;
	for (int i = 0; i < N; i++) {
		FindMin(A,min1,min2,num);
		A[num].K = A[min1].K + A[min2].K;
		A[num].Lc = min1;
		A[num].Rc = min2;
		A[num].IsRoot = true;
		A[min1].IsRoot = false;
		A[min2].IsRoot = false;
		A[num].L = 'h' + y;
		y++; num++;
	}
	cout << "最终权值为：" << A[14].K << endl;
}

确定结构体

首先我们创建结点 Node 结构体，并给他定义了五个属性，分别是字符、权值、布尔型根结点标志、以及左右子树。随后直接定义Node类型数组Node(char l,int k,bool isRoot)，初始化Node A数组的长度为 N+N-1的原因是：选取两个最小权值生成新的结点，并把结点放入A数组中，相当于每两个结点会多生成一个节点，那么n个结点就会生成n-1个结点，总数就是n+n-1；我们依次把八个结点放入数组中，并把IsRoot置为true，初始结点均没有参加生成新节点，都是根结点。

循环找出最小值

将A传入找最小值的函数，初始num为N，随着新节点的生成，逐渐++，然后默认最小值为数组的最后一个元素，利用一重for循环遍历出最小值和次小值，这里注意，找出的最小值必须是根结点才可以，参加过生成新结点的都要把IsRoot设为false，次小值就是在不等于最小值的情况下找出最小值。

调用细节

主函数中利用一重for循环调用FindMin函数找出两个最小权值结点并默认放到数组的num位置上，即为最后一个位置；首先新节点的权值由两个最小权值相加，并把新节点的左右子树设为找到的两个最小权值结点，由于结构体数组默认IsRoot为false，所有要把新节点设为根结点，而把用过的结点取消根结点身份，L用来更换结点的字符，最后num++,y++都很好理解，经过七次新节点的生成，我们不难猜到A[14]的权值k为100；

调试试图

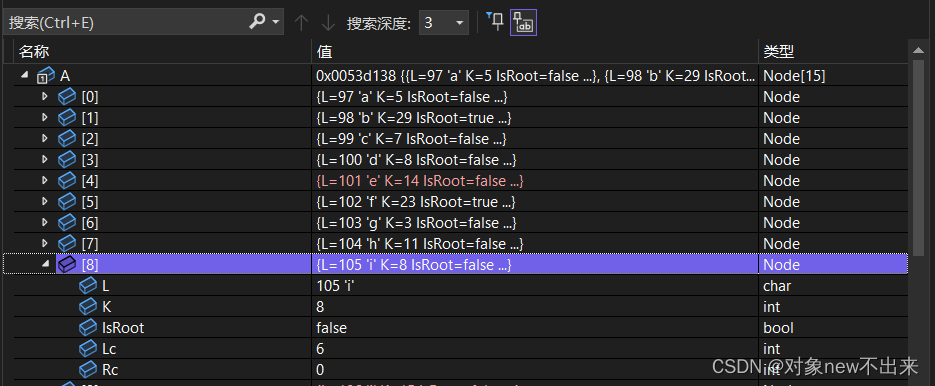
通过调试界面可以看到第一个生成的A[8]结点的左右子树是A[0]和A[6]，而且权值正好是他们两个结点的权相加；

A[9]的k是新的两个最小根结点A[2]和A[8]组成的，可以确认权值没有问题，A[8]能参加新节点的合成说明我们成功的把他设置为了根结点，然后直接看最后一个结点的信息；

权值正确为100，是根节点，因为只有一个根结点，没法继续合成新节点，程序结束。

总结

哈夫曼在算法和数据结构中都挺重要的，只是不同场景下实现的方法和形式会有所不同，但就算千变万化也离不开最基础的“二合一”形式，我提出的这个哈夫曼是不难理解的，希望对大家有所帮助，共同进步！！！

到此这篇关于C++使用数组来实现哈夫曼树的文章就介绍到这了,更多相关C++哈夫曼树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • C++链式二叉树深入分析

    C++链式二叉树深入分析

    目录 二叉树的结构和概念 二叉树的操作 前序遍历 中序遍历和后序遍历 二叉树的节点个数 求二叉树叶子结点个数 求二叉树的深度 在二叉树查找为X的结点 之前我们的重点学习二叉树都是完全二叉树,接下来我们来说下普通二叉树,普通的二叉树如果我们使用数组存储,那么会浪费相当多的空间的,所以我们选择链表存储,我们先再来复习下二叉树的结构吧. 二叉树的结构和概念 二叉树概念是: 1. 空树 2. 非空:根节点,根节点的左子树.根节点的右子树组成的. 从概念中可以看出,二叉树定义是递归式的. 我们就手动创建一

  • C++关于树的定义全面梳理

    C++关于树的定义全面梳理

    目录 概念 树 树的叶子节点 节点的度 分支结点 树的度 树的高度 树的深度 二叉树 二叉树的特点 满二叉树 完全二叉树 二叉查找树 示例 代码实现 开发环境 运行结果 概念 本文以一个简单的树为例,如下图,来记录树的一些概念. 树 一种由n个节点组成的具有一定层次关系的有限数据集合.每个节点有0个或者n个子节点,有一个根节点(没有前驱只有后继),除根节点外每一个节点都有一个前驱,0个或多个后继. 树的叶子节点 只有一个前驱,没有后继的节点,为最外层的节点.叶子节点的度为0. 节点的度 节点拥有

  • C++简单又轻松建立链式二叉树流程

    C++简单又轻松建立链式二叉树流程

    目录 递归建立二叉树 二叉树的结构体 二叉树初始化 先序遍历 中序遍历 后序遍历 具体例题 输入的格式 全部源码 总结 递归建立二叉树 二叉树的结构体 typedef struct Node { int data; Node* lchild; Node* rchild; }BiNode,*BiTree; 二叉树顾名思义最多只有两个子结点和一个数据域,既然是链式那么子结点定义为结点指针类型,数据域就可以根据需要设置了,可以是整型也可以是字符型. 二叉树初始化 BiTree createBiTree

  • C++深入讲解哈夫曼树

    C++深入讲解哈夫曼树

    目录 哈夫曼树的基本概念 1)路径 2)路径长度 3)权 4)结点的带权路径长度 5)树的带权路径长度 6)哈夫曼树 哈夫曼树的构造算法 哈夫曼树的构造过程 哈夫曼树算法的实现 1)结点的存储结构 2)构建哈夫曼树 哈夫曼树的基本概念 Q:什么是哈夫曼树 A:哈夫曼树又称最优树,是一类带权路径长度最短的树.在正式了解哈夫曼树之前,我们需要了解一些概念. 1)路径 Q:什么是路径 A:从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径. 2)路径长度 Q:什么是路径长度 A:路径上的分支

  • C++数据结构之AVL树的实现

    C++数据结构之AVL树的实现

    目录 1.概念 (1)二叉搜索树的缺点 (2)定义节点 2.插入 (1)拆分 (2)找节点与插节点 (3)更新平衡因子与旋转 3.判断 4.完整代码及测试代码 完整代码 测试代码 1.概念 (1)二叉搜索树的缺点 要手撕AVL树,我们首先要知道什么是AVL树.AVL树是在二叉搜索树的基础之上改造的.当我们插入的是一个有序的序列的时候,二叉搜素树会使用一条直线来进行存储,这样并不利于查找. 当遇到这种情况的时候我们就需要对这棵树来进行调整.AVL树会通过旋转等操作,来规避这种情况.最终满足每一个节

  • C++超详细实现二叉树的遍历

    C++超详细实现二叉树的遍历

    目录 二叉树的遍历 前序遍历 中序遍历 后序遍历 层序遍历 二叉树的遍历 Q:什么是二叉树的遍历? A:二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次,且仅被访问一次. Q:二叉树有几种遍历方法? A:二叉树的遍历方法可以有很多种,如果限制了从左到右的习惯方式,那么主要分为以下四种:先序遍历,中序遍历,后序遍历,层序遍历. 前序遍历 Q:什么是先序遍历 A:先序遍历就是先访问树的根节点,再访问树的左子节点,再访问右子节点.可以想象为,从一棵二叉树根节点

  • C++超详细讲解树与二叉树

    C++超详细讲解树与二叉树

    目录 树 树的定义 树的名词解释 树的表示 树的存储结构 二叉树的概念及结构 二叉树的概念 二叉树的性质 二叉树的存储结构 顺序存储结构 链式存储结构 树 树的定义 Q:什么是树 A:树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合.把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的. Q:树有什么特点 有一个特殊的结点,称为根结点,根节点没有前驱结点. 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1.T2.…….T

  • C++深入细致探究二叉搜索树

    C++深入细致探究二叉搜索树

    目录 1.二叉搜索树的概念 2.二叉搜索树的操作 二叉搜索树的查找 二叉搜索树的插入 二叉搜索树的删除 3.二叉搜索树的实现 4.二叉搜索树的性能分析 1.二叉搜索树的概念  二叉搜索树又称二叉排序树,它可以是一颗空树,亦可以是一颗具有如下性质的二叉树:   ①若根节点的左子树不为空,则左子树上的所有节点的值域都小于根节点的值   ②若根节点的右子树不为空,则右子树上的所有节点的值域都大于根节点的值   ③根节点的左右子树分别也是一颗二叉搜索树 例如下面的这棵二叉树就是一棵二叉搜索树: 注意:判

  • C++详细实现红黑树流程详解

    C++详细实现红黑树流程详解

    目录 红黑树的概念 红黑树的性质 红黑树的定义与树结构 插入 新增结点插入后维护红黑树性质的主逻辑 旋转 验证 红黑树与AVl树的比较 红黑树的应用 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black. 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的 概念总结: 红黑树是二叉搜索树的升级,结点里面存放的成员col标记当前结点的颜色,它的最长路径最多是最短路径的二倍,红黑

  • C++使用数组来实现哈夫曼树

    C++使用数组来实现哈夫曼树

    目录 写在前面 构造思想 算法设计 构造实例 理解代码 确定结构体 循环找出最小值 调用细节 调试试图 总结 写在前面 哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树.所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数).树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶

  • 解析C++哈夫曼树编码和译码的实现

    解析C++哈夫曼树编码和译码的实现

    一．背景介绍: 给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree).哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近. 二．实现步骤: 1.构造一棵哈夫曼树 2.根据创建好的哈夫曼树创建一张哈夫曼编码表 3.输入一串哈夫曼序列,输出原始字符 三．设计思想: 1.首先要构造一棵哈夫曼树,哈夫曼树的结点结构包括权值,双亲,左右孩子:假如由n个字符来构造一棵哈夫曼树,则共有结点2n-1个:在构造前,先初始化

  • 使用C语言详解霍夫曼树数据结构

    使用C语言详解霍夫曼树数据结构

    1.基本概念 a.路径和路径长度 若在一棵树中存在着一个结点序列 k1,k2,--,kj, 使得 ki是ki+1 的双亲(1<=i<j),则称此结点序列是从 k1 到 kj 的路径. 从 k1 到 kj 所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1. b.结点的权和带权路径长度 在许多应用中,常常将树中的结点赋予一个有着某种意义的实数,我们称此实数为该结点的权,(如下面一个树中的蓝色数字表示结点的权) 结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘

  • C++数据结构之文件压缩（哈夫曼树）实例详解

    C++数据结构之文件压缩(哈夫曼树)实例详解 概要: 项目简介:利用哈夫曼编码的方式对文件进行压缩,并且对压缩文件可以解压 开发环境:windows vs2013 项目概述:         1.压缩 a.读取文件,将每个字符,该字符出现的次数和权值构成哈夫曼树 b.哈夫曼树是利用小堆构成,字符出现次数少的节点指针存在堆顶,出现次数多的在堆底 c.每次取堆顶的两个数,再将两个数相加进堆,直到堆被取完,这时哈夫曼树也建成 d.从哈夫曼树中获取哈夫曼编码,然后再根据整个字符数组来获取出现了得字符的编

  • C语言实现哈夫曼树

    本文实例为大家分享了C语言实现哈夫曼树的具体代码,供大家参考,具体内容如下 //哈夫曼树C语言实现 #include <stdio.h> #include <stdlib.h> typedef struct HuffmanNode { char letter;//存储的字符,叶节点为字母,非叶节点为# struct HuffmanNode *parent;//父亲结点 int code;//如果为父亲结点的左孩子,则为0,右孩子为1 }HuffmanNode; typedef st

  • C++实现哈夫曼树编码解码

    本文实例为大家分享了C++实现哈夫曼树的编码解码,供大家参考,具体内容如下 代码: #pragma once #include<iostream> #include<stack> using namespace std; #define m 20 stack<int> s; /*哈夫曼树结点类HuffmanNode声明*/ template<class T> class HuffmanNode { private: HuffmanNode<T>

  • C++实现哈夫曼树的方法

    序言 对于哈夫曼编码,个人的浅薄理解就是在压缩存储空间用很大用处. 用一个很简单例子,存储一篇英文文章时候,可能A出现的概率较大,Z出现的记录较小,如果正常存储,可能A与Z存储使用的空间一样.但是用哈夫曼编码方式,A经常出现,所用编码长度就短. 构造哈夫曼树,生成哈夫曼编码 一.定义节点类型 struct Node { char C; long key; Node *Left, *Right,*parent; Node() { Left = Right = NULL; } }; 二.定义树类型(

  • C语言实现哈夫曼树的构建

    哈夫曼树(霍夫曼树)又称为最优树. 1.路径和路径长度 在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径.通路中分支的数目称为路径长度.若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1. 2.结点的权及带权路径长度 若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权.结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积. 3.树的带权路径长度 树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL #include

  • C语言实现哈夫曼树的方法

    C语言实现哈夫曼树的方法

    本文实例为大家分享了C语言实现哈夫曼树的具体代码,供大家参考,具体内容如下 准备工作: 1.定义一个结构体,表示一个节点.其中,这个结构体有4个成员变量,分别表示是这个节点的权值,父节点及左右子节点的下标 2.定义一个整形数组,用于存放各个节点的权值 3.定义一个整形数组,用于存放哈夫曼编码,当然也可以定义一个整形数组来存放哈夫曼编码 构建哈夫曼树: 1.给这个哈夫曼树创建一个结构体数组,其中分配的空间是2 * n - 1,因为我们都知道哈夫曼树的性质有一个是:给定n个叶子节点,那么由这n个叶子

  • Java数据结构之哈夫曼树概述及实现

    Java数据结构之哈夫曼树概述及实现

    一.与哈夫曼树相关的概念 概念 含义 1. 路径 从树中一个结点到另一个结点的分支所构成的路线 2. 路径长度 路径上的分支数目 3. 树的路径长度 长度从根到每个结点的路径长度之和 4. 带权路径长度 结点具有权值, 从该结点到根之间的路径长度乘以结点的权值, 就是该结点的带权路径长度 5. 树的带权路径长度 树中所有叶子结点的带权路径长度之和 二.什么是哈夫曼树 定义: 给定n个权值作为n个叶子结点, 构造出的一棵带权路径长度(WPL)最短的二叉树,叫哈夫曼树(), 也被称为最最优二叉树.

随机推荐