TensorFlow 多元函数的极值实例
flyfish
python实现
设函数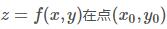
的某个邻域内有定义，对于该邻域内异于的点，如果都适合不等式
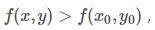
则称函数在点有极大值。
如果都适合不等式
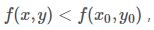
则称函数在点有极小值．
极大值、极小值统称为极值。使函数取得极值的点称为极值点。
有极小值的例子
函数
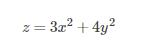
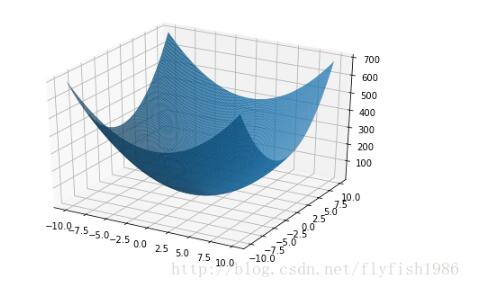
在点（0，0）处有极小值。因为对于点 (0,0)的任一邻域内异于(0,0)的点，函数值都为正，而在点(0,0)处的函数值为零。从几何上看这是显然的，因为点(0,0,0)是开口朝上的椭圆抛物面
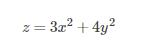
的顶点。
代码
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) X = np.arange(-10, 10, 0.1) Y = np.arange(-10, 10, 0.1) X, Y = np.meshgrid(X, Y) Z = (3*X**2 + 4*Y**2) ax.plot_surface(X, Y, Z, rstride=1, cstride=1) plt.show()
有极大值的例子
函数
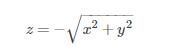
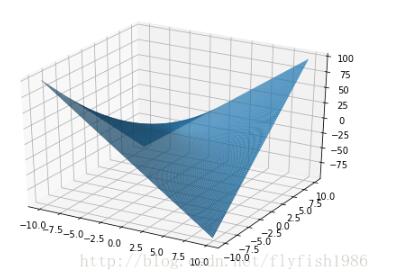
在点（0，0）处有极大值。因为在点（0，0）处函数值为零，而对于点（0，0）的任一邻域内异于（0，0）的点，函数值都为负，点（0，0，0）是位于xOy平面下方的锥面$$z=-\sqrt{x^2+y^2}的顶点。
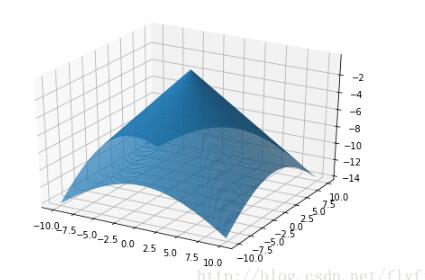
代码
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) X = np.arange(-10, 10, 0.1) Y = np.arange(-10, 10, 0.1) X, Y = np.meshgrid(X, Y) Z = np.sqrt(X**2 + Y**2)*(-1) ax.plot_surface(X, Y, Z, rstride=1, cstride=1) plt.show()
没有极大值也没有极小值的例子
函数z=xy在点（0，0）处既不取得极大值也不取得极小值。因为在点（0，0）处的函数值为零，而在点（0，0）的任一邻域内，总有使函数值为正的点，也有使函
数值为负的点。
像一个马鞍的图形
代码
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) X = np.arange(-10, 10, 0.1) Y = np.arange(-10, 10, 0.1) X, Y = np.meshgrid(X, Y) Z = X*Y ax.plot_surface(X, Y, Z, rstride=1, cstride=1) plt.show()
以上这篇TensorFlow 多元函数的极值实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。
赞 (0)