使用python模拟高斯分布例子

正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution）

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

用python 模拟

#!/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
from scipy import stats
import math
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import seaborn

def calc_statistics(x):
  n = x.shape[0] # 样本个数
  # 手动计算
  m = 0
  m2 = 0
  m3 = 0
  m4 = 0
  for t in x:
    m += t
    m2 += t*t
    m3 += t**3
    m4 += t**4
  m /= n
  m2 /= n
  m3 /= n
  m4 /= n

  mu = m
  sigma = np.sqrt(m2 - mu*mu)
  skew = (m3 - 3*mu*m2 + 2*mu**3) / sigma**3
  kurtosis = (m4 - 4*mu*m3 + 6*mu*mu*m2 - 4*mu**3*mu + mu**4) / sigma**4 - 3
  print('手动计算均值、标准差、偏度、峰度：', mu, sigma, skew, kurtosis)

  # 使用系统函数验证
  mu = np.mean(x, axis=0)
  sigma = np.std(x, axis=0)
  skew = stats.skew(x)
  kurtosis = stats.kurtosis(x)
  return mu, sigma, skew, kurtosis

if __name__ == '__main__':
  d = np.random.randn(10000)
  print(d)
  print(d.shape)
  mu, sigma, skew, kurtosis = calc_statistics(d)
  print('函数库计算均值、标准差、偏度、峰度：', mu, sigma, skew, kurtosis)
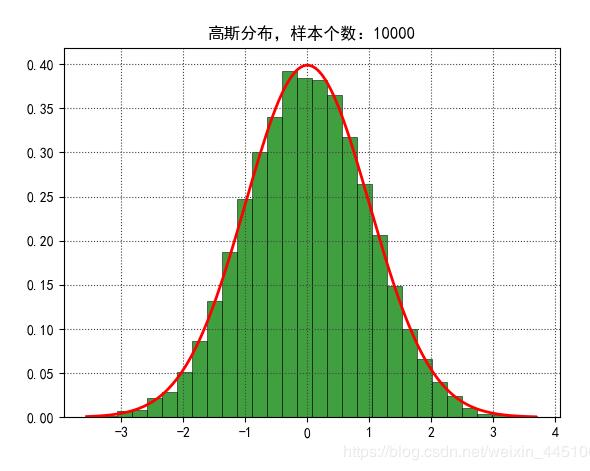
  # 一维直方图
  mpl.rcParams['font.sans-serif'] = 'SimHei'
  mpl.rcParams['axes.unicode_minus'] = False
  plt.figure(num=1, facecolor='w')
  y1, x1, dummy = plt.hist(d, bins=30, normed=True, color='g', alpha=0.75, edgecolor='k', lw=0.5)
  t = np.arange(x1.min(), x1.max(), 0.05)
  y = np.exp(-t**2 / 2) / math.sqrt(2*math.pi)
  plt.plot(t, y, 'r-', lw=2)
  plt.title('高斯分布，样本个数：%d' % d.shape[0])
  plt.grid(b=True, ls=':', color='#404040')
  # plt.show()

  d = np.random.randn(100000, 2)
  mu, sigma, skew, kurtosis = calc_statistics(d)
  print('函数库计算均值、标准差、偏度、峰度：', mu, sigma, skew, kurtosis)

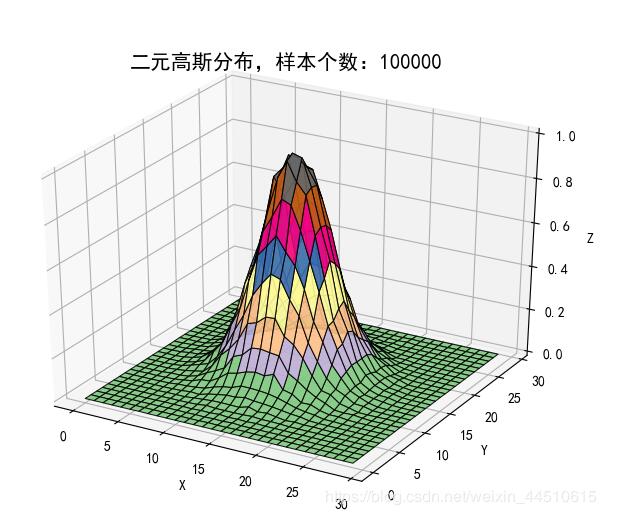
  # 二维图像
  N = 30
  density, edges = np.histogramdd(d, bins=[N, N])
  print('样本总数：', np.sum(density))
  density /= density.max()
  x = y = np.arange(N)
  print('x = ', x)
  print('y = ', y)
  t = np.meshgrid(x, y)
  print(t)
  fig = plt.figure(facecolor='w')
  ax = fig.add_subplot(111, projection='3d')
  # ax.scatter(t[0], t[1], density, c='r', s=50*density, marker='o', depthshade=True, edgecolor='k')
  ax.plot_surface(t[0], t[1], density, cmap=cm.Accent, rstride=1, cstride=1, alpha=0.9, lw=0.75, edgecolor='k')
  ax.set_xlabel('X')
  ax.set_ylabel('Y')
  ax.set_zlabel('Z')
  plt.title('二元高斯分布，样本个数：%d' % d.shape[0], fontsize=15)
  plt.tight_layout(0.1)
  plt.show()

来个6的

二元高斯分布方差比较

#!/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
from scipy import stats
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

if __name__ == '__main__':
  x1, x2 = np.mgrid[-5:5:51j, -5:5:51j]
  x = np.stack((x1, x2), axis=2)
  print('x1 = \n', x1)
  print('x2 = \n', x2)
  print('x = \n', x)

  mpl.rcParams['axes.unicode_minus'] = False
  mpl.rcParams['font.sans-serif'] = 'SimHei'
  plt.figure(figsize=(9, 8), facecolor='w')
  sigma = (np.identity(2), np.diag((3,3)), np.diag((2,5)), np.array(((2,1), (1,5))))
  for i in np.arange(4):
    ax = plt.subplot(2, 2, i+1, projection='3d')
    norm = stats.multivariate_normal((0, 0), sigma[i])
    y = norm.pdf(x)
    ax.plot_surface(x1, x2, y, cmap=cm.Accent, rstride=1, cstride=1, alpha=0.9, lw=0.3, edgecolor='#303030')
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
  plt.suptitle('二元高斯分布方差比较', fontsize=18)
  plt.tight_layout(1.5)
  plt.show()

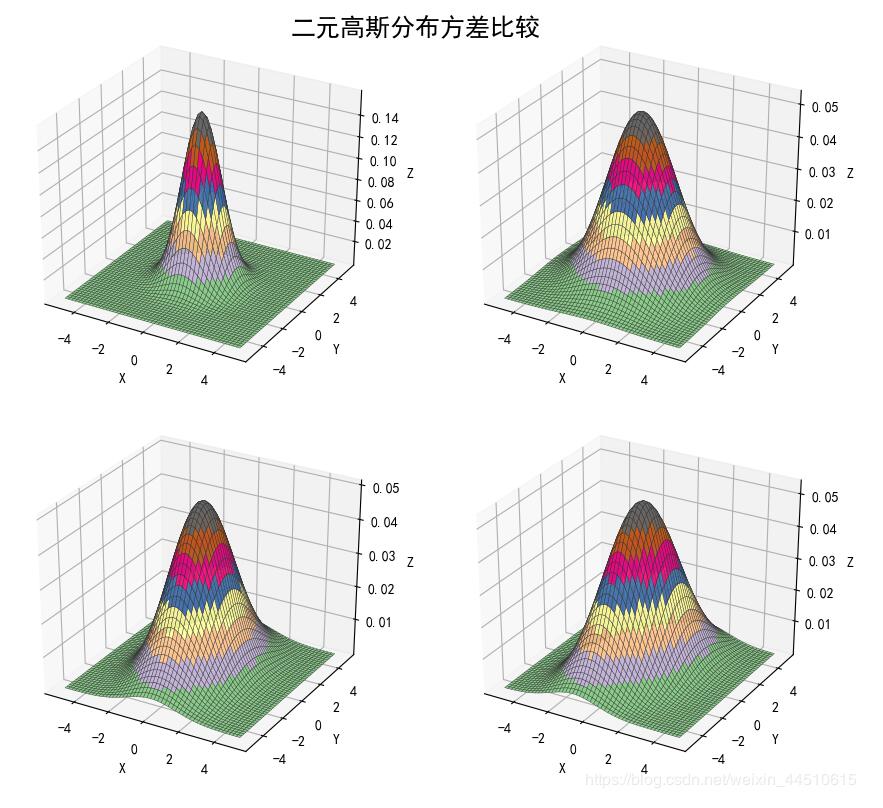
图像好看吗？

以上这篇使用python模拟高斯分布例子就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。