KMP算法最浅显理解(小白教程)

说明

KMP算法看懂了觉得特别简单，思路很简单，看不懂之前，查各种资料，看的稀里糊涂，即使网上最简单的解释，依然看的稀里糊涂。
我花了半天时间，争取用最短的篇幅大致搞明白这玩意到底是啥。
这里不扯概念，只讲算法过程和代码理解：

KMP算法求解什么类型问题

字符串匹配。给你两个字符串，寻找其中一个字符串是否包含另一个字符串，如果包含，返回包含的起始位置。
如下面两个字符串：

char *str = "bacbababadababacambabacaddababacasdsd";
char *ptr = "ababaca";

str有两处包含ptr
分别在str的下标10，26处包含ptr。

“bacbababadababacambabacaddababacasdsd”;\

问题类型很简单，下面直接介绍算法

算法说明

一般匹配字符串时，我们从目标字符串str（假设长度为n）的第一个下标选取和ptr长度（长度为m）一样的子字符串进行比较，如果一样，就返回开始处的下标值，不一样，选取str下一个下标，同样选取长度为n的字符串进行比较，直到str的末尾（实际比较时，下标移动到n-m）。这样的时间复杂度是O(n*m)。

KMP算法：可以实现复杂度为O(m+n)

为何简化了时间复杂度：
充分利用了目标字符串ptr的性质（比如里面部分字符串的重复性，即使不存在重复字段，在比较时，实现最大的移动量）。
上面理不理解无所谓，我说的其实也没有深刻剖析里面的内部原因。

考察目标字符串ptr：
ababaca
这里我们要计算一个长度为m的转移函数next。

next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。

比如：abcjkdabc，那么这个数组的最长前缀和最长后缀相同必然是abc。
cbcbc，最长前缀和最长后缀相同是cbc。
abcbc，最长前缀和最长后缀相同是不存在的。

**注意最长前缀：是说以第一个字符开始，但是不包含最后一个字符。
比如aaaa相同的最长前缀和最长后缀是aaa。**
对于目标字符串ptr，ababaca，长度是7，所以next[0]，next[1]，next[2]，next[3]，next[4]，next[5]，next[6]分别计算的是
a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀的长度。由于a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀是“”，“”，“a”，“ab”，“aba”，“”，“a”,所以next数组的值是[-1,-1,0,1,2,-1,0]，这里-1表示不存在，0表示存在长度为1，2表示存在长度为3。这是为了和代码相对应。

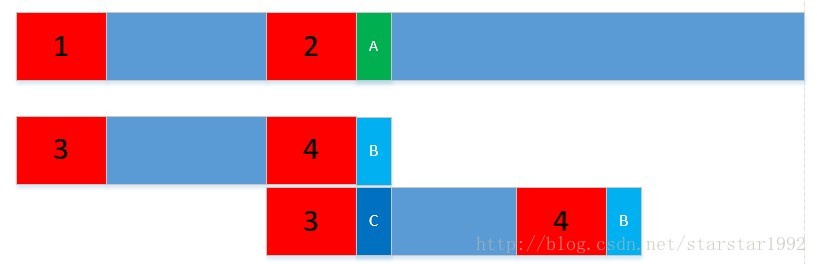
下图中的1，2，3，4是一样的。1-2之间的和3-4之间的也是一样的，我们发现A和B不一样；之前的算法是我把下面的字符串往前移动一个距离，重新从头开始比较，那必然存在很多重复的比较。现在的做法是，我把下面的字符串往前移动，使3和2对其，直接比较C和A是否一样。

代码解析

void cal_next(char *str, int *next, int len)
{
  next[0] = -1;//next[0]初始化为-1，-1表示不存在相同的最大前缀和最大后缀
  int k = -1;//k初始化为-1
  for (int q = 1; q <= len-1; q++)
  {
    while (k > -1 && str[k + 1] != str[q])//如果下一个不同，那么k就变成next[k]，注意next[k]是小于k的，无论k取任何值。
    {
      k = next[k];//往前回溯
    }
    if (str[k + 1] == str[q])//如果相同，k++
    {
      k = k + 1;
    }
    next[q] = k;//这个是把算的k的值（就是相同的最大前缀和最大后缀长）赋给next[q]
  }
}

KMP

这个和next很像，具体就看代码，其实上面已经大概说完了整个匹配过程。

int KMP(char *str, int slen, char *ptr, int plen)
{
  int *next = new int[plen];
  cal_next(ptr, next, plen);//计算next数组
  int k = -1;
  for (int i = 0; i < slen; i++)
  {
    while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配，且k>-1（表示ptr和str有部分匹配）
      k = next[k];//往前回溯
    if (ptr[k + 1] == str[i])
      k = k + 1;
    if (k == plen-1)//说明k移动到ptr的最末端
    {
      //cout << "在位置" << i-plen+1<< endl;
      //k = -1;//重新初始化，寻找下一个
      //i = i - plen + 1;//i定位到该位置，外层for循环i++可以继续找下一个（这里默认存在两个匹配字符串可以部分重叠），感谢评论中同学指出错误。
      return i-plen+1;//返回相应的位置
    }
  }
  return -1;
}

测试

  char *str = "bacbababadababacambabacaddababacasdsd";
  char *ptr = "ababaca";
  int a = KMP(str, 36, ptr, 7);
  return 0;

注意如果str里有多个匹配ptr的字符串，要想求出所有的满足要求的下标位置，在KMP算法需要稍微修改一下。见上面注释掉的代码。

复杂度分析

next函数计算复杂度是(m)，开始以为是O(m^2)，后来仔细想了想，cal__next里的while循环，以及外层for循环，利用均摊思想，其实是O(m)，这个以后想好了再写上。

………………………………………..分割线……………………………………..
其实本文已经结束，后面的只是针对评论里的疑问，我尝试着进行解答的。

进一步说明（2018-3-14）

看了评论，大家对cal_next(..)函数和KMP()函数里的

while (k > -1 && str[k + 1] != str[q])
    {
      k = next[k];
    }

和

while (k >-1&& ptr[k + 1] != str[i])
      k = next[k];

这个while循环和k=next[k]很疑惑！
确实啊，我开始看这几行代码，相当懵逼，这写的啥啊，为啥这样写；后来上机跑了一下，慢慢了解到为何这样写了。这几行代码，可谓是对KMP算法本质得了解非常清楚才能想到的。很牛逼！
直接看cal_next(..)函数：
首先我们看第一个while循环，它到底干了什么。

在此之前，我们先回到原程序。原程序里有一个大的for()循环，那这个for()循环是干嘛的？

这个for循环就是计算next[0]，next[1],…next[q]…的值。

里面最后一句next[q]=k就是说明每次循环结束，我们已经计算了ptr的前(q+1)个字母组成的子串的“相同的最长前缀和最长后缀的长度”。（这句话前面已经解释了！） 这个“长度”就是k。

好，到此为止，假设循环进行到 第 q 次，即已经计算了next[q]，我们是怎么计算next[q+1]呢？

比如我们已经知道ababab，q=4时，next[4]=2（k=2，表示该字符串的前5个字母组成的子串ababa存在相同的最长前缀和最长后缀的长度是3，所以k=2,next[4]=2。这个结果可以理解成我们自己观察算的，也可以理解成程序自己算的，这不是重点，重点是程序根据目前的结果怎么算next[5]的）.，那么对于字符串ababab，我们计算next[5]的时候，此时q=5, k=2（上一步循环结束后的结果）。那么我们需要比较的是str[k+1]和str[q]是否相等，其实就是str[1]和str[5]是否相等！，为啥从k+1比较呢，因为上一次循环中，我们已经保证了str[k]和str[q]（注意这个q是上次循环的q）是相等的（这句话自己想想，很容易理解），所以到本次循环，我们直接比较str[k+1]和str[q]是否相等（这个q是本次循环的q）。
如果相等，那么跳出while()，进入if()，k=k+1，接着next[q]=k。即对于ababab，我们会得出next[5]=3。 这是程序自己算的，和我们观察的是一样的。
如果不等，我们可以用”ababac“描述这种情况。 不等，进入while()里面，进行k=next[k]，这句话是说，在str[k + 1] != str[q]的情况下，我们往前找一个k，使str[k + 1]==str[q]，是往前一个一个找呢，还是有更快的找法呢？ （一个一个找必然可以，即你把 k = next[k] 换成k- -也是完全能运行的（更正：这句话不对啊，把k=next[k]换成k–是不行的，评论25楼举了个反例）。但是程序给出了一种更快的找法，那就是 k = next[k]。 程序的意思是说，一旦str[k + 1] != str[q]，即在后缀里面找不到时，我是可以直接跳过中间一段，跑到前缀里面找，next[k]就是相同的最长前缀和最长后缀的长度。所以，k=next[k]就变成，k=next[2]，即k=0。此时再比较str[0+1]和str[5]是否相等，不等，则k=next[0]=-1。跳出循环。
（这个解释能懂不？）

以上就是这个cal_next()函数里的

while (k > -1 && str[k + 1] != str[q])
    {
      k = next[k];
    }

最难理解的地方的一个我的理解，有不对的欢迎指出。

复杂度分析：

分析KMP复杂度，那就直接看KMP函数。

int KMP(char *str, int slen, char *ptr, int plen)
{
  int *next = new int[plen];
  cal_next(ptr, next, plen);//计算next数组
  int k = -1;
  for (int i = 0; i < slen; i++)
  {
    while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配，且k>-1（表示ptr和str有部分匹配）
      k = next[k];//往前回溯
    if (ptr[k + 1] == str[i])
      k = k + 1;
    if (k == plen-1)//说明k移动到ptr的最末端
    {
      //cout << "在位置" << i-plen+1<< endl;
      //k = -1;//重新初始化，寻找下一个
      //i = i - plen + 1;//i定位到该位置，外层for循环i++可以继续找下一个（这里默认存在两个匹配字符串可以部分重叠），感谢评论中同学指出错误。
      return i-plen+1;//返回相应的位置
    }
  }
  return -1;
}

这玩意真的不好解释，简单说一下：

从代码解释复杂度是一件比较难的事情，我们从

这个图来解释。

我们可以看到，匹配串每次往前移动，都是一大段一大段移动，假设匹配串里不存在重复的前缀和后缀，即next的值都是-1，那么每次移动其实就是一整个匹配串往前移动m个距离。然后重新一一比较，这样就比较m次，概括为，移动m距离，比较m次，移到末尾，就是比较n次，O(n)复杂度。 假设匹配串里存在重复的前缀和后缀，我们移动的距离相对小了点，但是比较的次数也小了，整体代价也是O(n)。
所以复杂度是一个线性的复杂度。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。