Java 超详细讲解数据结构中的堆的应用

2024-09-28 11:16:00

一、堆的创建

1、向下调整（以小堆为例）

让parent标记需要调整的节点，child标记parent的左孩子(注意：parent如果有孩子一定先是有左孩子)

如果parent的左孩子存在，即:child < size，进行以下操作，直到parent的左孩子不存在：

parent右孩子是否存在，存在找到左右孩子中最小的孩子，让child进行标记
将parent与较小的孩子child比较，如果：

parent小于较小的孩子child，调整结束否则：交换parent与较小的孩子child，交换完成之后，parent中大的元素向下移动，可能导致子树不满足堆的性质，因此需要继续向下调整，即parent = child；child = parent*2+1; 然后继续2。

public void shiftDown(int[] elem,int parent,int len){
        int cur=parent*2+1;
        while(cur<len){
           if(cur+1<len){
               if(elem[cur+1]<elem[cur]){
                   cur++;
               }
           }
            if(this.elem[cur]<this.elem[parent]) {
                swap(cur, parent);
            }
            parent=cur;
            cur=parent*2+1;
        }
    }

2、创建堆

对于普通序列，我们需要从它的第一个有左节点的父节点开始调整，知道整棵树满足堆的性质。

3、创建堆的时间复杂度

堆必须是完全二叉树，满二叉树也是完全二叉树。由下面的计算，创建堆的时间复杂度为O(n).

二、堆的插入和删除

1、堆的插入

将要插入的元素放在堆的最后，如果放不了，进行扩容
将新插入的节点向上调整，直到满足堆的性质

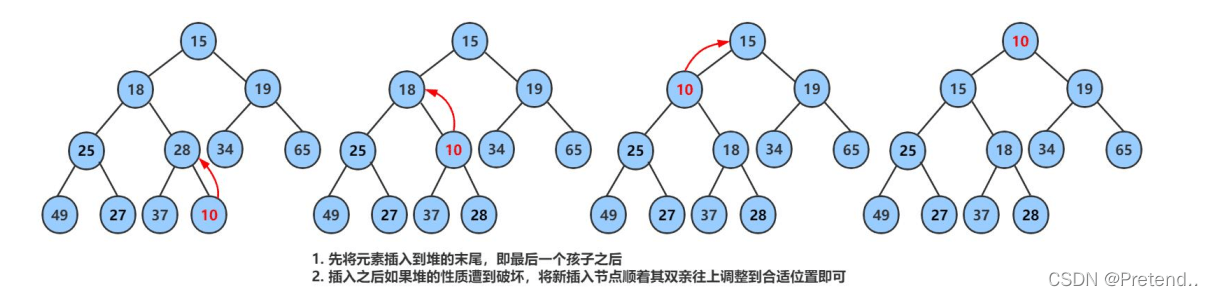
【向上调整】

public void shiftUp(int elem[],int child){
        int parent=(child-1)/2;
        while(parent>=0){
            if(elem[child]>elem[parent]){
                swap(child,parent);
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

2、堆的删除

根据堆的性质，对删除的一定是堆顶元素。步骤如下：

将堆顶元素和最后一个元素交换
堆的元素个数减一
对堆顶元素进行向下调整

三、堆的应用

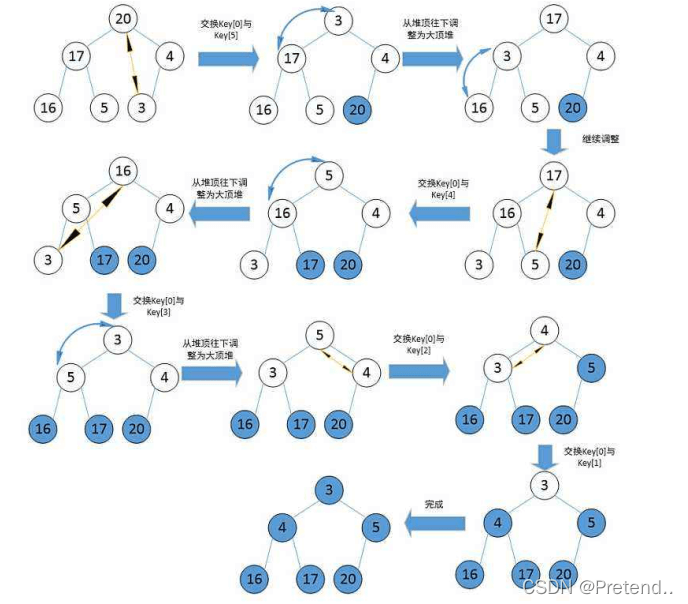
1、堆排序

升序：创建大根堆

降序：创建小根堆

交换堆顶元素和堆得最后一个元素，进行向下调整，直到堆有序。

2、top-k问题【求最小的K个数】

top-k问题：求数据集合中前k个大或者小的元素，一般数据量都比较大。

class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] array=new int[k];
        if(arr==null||arr.length<=k||k==0){
            return array;
        }
        PriorityQueue<Integer> queue=new PriorityQueue<>((a,b)->b-a);
        int i=0;
        for(;i<k;++i){
            queue.offer(arr[i]);
        }
        while(i<arr.length){
            if(arr[i]<queue.peek()){
                queue.poll();
                queue.offer(arr[i]);
            }
            i++;
        }
        int size=queue.size();
        for(int j=0;j<size;++j){
            array[j]=queue.poll();
        }
        return array;
    }
}

四、常用接口的介绍

1、PriorityQueue的特性

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列。PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的，本文主要介绍PriorityQueue。

【PriorityQueue】使用的注意事项：

必须导入PeioriryQueue的包；
放置的元素必须是能够比较大小的，否则会抛出ClassCastException异常；
不能放置null元素，否则会抛出NullPointerException；
可以插入任意多的元素，内部会自动扩容；
底层使用了堆数据结构，默认是小堆。如果要构建大堆，则需要提供比较器。

PriorityQueue的扩容方式：

如果容量小于64时，是按照oldCapacity的2倍方式扩容的
如果容量大于等于64，是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进行扩容

int newCapacity = oldCapacity + ((oldCapacity < 64) ?

(oldCapacity + 2) :

(oldCapacity >> 1));

PriorityQueue采用了：Comparble和Comparator两种方式。

1. Comparble是默认的内部比较方式，如果用户插入自定义类型对象时，该类对象必须要实现Comparble接口，并覆写compareTo方法

2. 用户也可以选择使用比较器对象，如果用户插入自定义类型对象时，必须要提供一个比较器类，让该类实现Comparator接口并覆写compare方法

// 用户自己定义的比较器：直接实现Comparator接口，然后重写该接口中的compare方法即可
class IntCmp implements Comparator<Integer>{
   @Override
   public int compare(Integer o1, Integer o2) {
      return o2-o1;
   }
}
PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());

2、优先级队列的构造

构造器	功能介绍
PriorityQueue()	创建一个空的优先级队列，默认容量是11
PriorityQueue(int initialCapacity)	创建一个初始容量为initialCapacity的优先级队列，注意： initialCapacity不能小于1，否则会抛IllegalArgumentException异常
PriorityQueue(Collection<? extends E> c)	用一个集合来创建优先级队列

到此这篇关于Java 超详细讲解数据结构中的堆的应用的文章就介绍到这了,更多相关Java 堆的应用内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

Java 数据结构与算法系列精讲之二叉堆

目录概述优先队列二叉堆二叉堆实现获取索引添加元素 siftUp 完整代码概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 优先队列优先队列 (Priority Queue) 和队列一样, 是一种先进先出的数据结构. 优先队列中的每个元素有各自的优先级, 优先级最高的元素最先得到服务. 如图: 二叉堆二叉堆 (Binary Heap) 是一种特殊的堆, 二叉堆具有堆的性质和二叉树的性质. 二叉堆中的任意一节点的值总是大于等于其孩子节点值. 如图: 二
java 数据结构之堆排序（HeapSort）详解及实例

1 堆排序堆是一种重要的数据结构,分为大根堆和小根堆,是完全二叉树, 底层如果用数组存储数据的话,假设某个元素为序号为i(Java数组从0开始,i为0到n-1),如果它有左子树,那么左子树的位置是2i+1,如果有右子树,右子树的位置是2i+2,如果有父节点,父节点的位置是(n-1)/2取整.最大堆的任意子树根节点不小于任意子结点,最小堆的根节点不大于任意子结点. 所谓堆排序就是利用堆这种数据结构的性质来对数组进行排序,在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的性质可知,最大的
Java 数据结构之堆的概念与应用

目录什么是堆堆的类型小根堆大根堆堆的基本操作:创建堆堆的时间复杂度和空间复杂度堆的应用-优先级队列概念优先级队列基本操作入优先级队列出优先级队列首元素 java的优先级队列堆的常见面试题最后一块石头的重量找到K个最接近的元素查找和最小的K对数字 java数据结构的堆什么是堆堆指的是使用数组保存完全二叉树结构,以层次遍历的方式放入数组中. 如图: 注意:堆方式适合于完全二叉树,对于非完全二叉树若使用堆则会造成空间的浪费对于根节点与其左右孩子在数组中的下标关系可表
Java深入了解数据结构之优先级队列(堆)

目录一,二叉树的顺序存储 ①存储方式 ②下标关系 ③二叉树顺序遍历二,堆 ①概念 ②操作-向下调整 ③建堆(建大堆为例) 三,堆的应用-优先级队列 ①概念 ②内部原理 ③入队列 ④出队列(优先级最高) ⑤返回队首元素(优先级最高) 四,堆排序一,二叉树的顺序存储 ①存储方式使用数组保存二叉树结构,方式即将二叉树用层序遍历方式放入数组中. 一般只适合表示完全二叉树,因为非完全二叉树会有空间的浪费. 这种方式的主要用法就是堆的表示. ②下标关系已知双亲(parent)的下标,则: 左孩子(
深入了解Java数据结构和算法之堆

目录 1.堆的定义 2.遍历和查找 3.移除 4.插入 5.完整的Java堆代码总结 1.堆的定义 ①.它是完全二叉树,除了树的最后一层节点不需要是满的,其它的每一层从左到右都是满的.注意下面两种情况,第二种最后一层从左到右中间有断隔,那么也是不完全二叉树. ②.它通常用数组来实现. 这种用数组实现的二叉树,假设节点的索引值为index,那么: 节点的左子节点是 2*index+1, 节点的右子节点是 2*index+2, 节点的父节点是 (index-1)/2. ③.堆中的每一个节点的关键字
Java数据结构之优先级队列(堆)图文详解

目录一.堆的概念二.向下调整 1.建初堆 2.建堆三.优先级队列 1.什么是优先队列? 2.入队列 3.出队列 4.返回队首元素 5.堆的其他TopK问题总结: 总结一.堆的概念堆的定义:n个元素的序列{k1 , k2 , … , kn}称之为堆,当且仅当满足以下条件时: (1)ki >= k2i 且 ki >= k(2i+1) ——大根堆 (2) ki <= k2i 且 ki <= k(2i+1) ——小根堆简单来说: 堆是具有以下性质的完全二叉树:(1)每个结点的
java数据结构-堆实现优先队列

目录一.二叉树的顺序存储 1.堆的存储方式 2.下标关系二.堆(heap) 1.概念 2.大/小根堆 2.1小根堆 2.2大根堆 3.建堆操作 3.1向下调整 4.入队操作 4.1向上调整 4.2push 入队的完整代码展示 5.出队操作 5.1pop 出队代码完全展示 6.查看堆顶元素 7.TOK 问题 7.1TOPK 8.堆排序文章内容介绍大纲一.二叉树的顺序存储 1.堆的存储方式使用数组保存二叉树结构,方式即将二叉树用层序遍历方式放入数组中. 一般只适合表示完全二叉树,因为非完
Java数据结构中堆的向下和向上调整解析

目录一.关于堆 1.堆的概念 2.堆的性质 3.堆的存储方式二.堆的创建 1.堆向下调整 2.堆的创建三.向上调整一.关于堆 JDK1.8中的PriortyQueue(优先级队列)底层使用了堆的数据结构,而堆实际就是在完全二叉树的基础之上进行了一些元素的调整. 1.堆的概念堆有最大堆和最小堆之分. 最大(最小)堆是一棵每一个节点的元素都不小于(大于)其孩子(如果存在)的元素的树.大堆是一棵完全二叉树,同时也是一棵最大树.小堆是一棵完全二叉树,同时也是一棵最小树. 注意: 堆中的任一子树
Java 超详细讲解数据结构中的堆的应用

目录一.堆的创建 1.向下调整(以小堆为例) 2.创建堆 3.创建堆的时间复杂度二.堆的插入和删除 1.堆的插入 2.堆的删除三.堆的应用 1.堆排序 2.top-k问题 [求最小的K个数] 四.常用接口的介绍 1.PriorityQueue的特性 2.优先级队列的构造一.堆的创建 1.向下调整(以小堆为例) 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子) 如果parent的左孩子存在,即:child < size,
Java 超详细讲解数据结构中的堆的应用

目录一.堆的创建 1.向下调整(以小堆为例) 2.创建堆 3.创建堆的时间复杂度二.堆的插入和删除 1.堆的插入 2.堆的删除三.堆的应用 1.堆排序 2.top-k问题(求最小的K个数) 四.常用接口的介绍 1.PriorityQueue的特性 2.优先级队列的构造一.堆的创建 1.向下调整(以小堆为例) 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子) 如果parent的左孩子存在,即:child < size, 进
C语言超详细讲解数据结构中双向带头循环链表

目录一.概念二.必备工作 2.1.创建双向链表结构 2.2.初始化链表 2.3.动态申请节点 2.4.打印链表 2.5.销毁链表三.主要功能 3.1.在pos节点前插入数据尾插头插 3.2.删除pos处节点数据尾删头删 3.3.查找数据四.总代码 List.h 文件 List.c 文件 Test.c 文件五.拓展一.概念前文我们已经学习了单向链表,并通过oj题目深入了解了带头节点的链表以及带环链表,来画张图总体回顾下: 在我们学习的链表中,其实总共有8种,都是单双向和带不带
C语言超详细讲解数据结构中的线性表

目录前言一.分文件编写 1.分文件编写概念 2.代码展示二.动态分布内存malloc 1.初识malloc 2.使用方法三.创建链表并进行增删操作 1.初始化链表 2.在链表中增加数据 3.删除链表中指定位置数据四.代码展示与运行效果 1.代码展示 2.运行效果总结前言计算机专业都逃不了数据结构这门课,而这门课无疑比较难理解,所以结合我所学知识,我准备对顺序表做一个详细的解答,为了避免代码过长,采用分文件编写的形式,不仅可以让代码干净利落还能提高代码可读性,先解释部分代码的含义,
Java超详细讲解SpringMVC如何获取请求数据

目录 1.获得请求参数 1)基本类型参数: 2)POJO类型参数: 3)数组类型参数 4)集合类型参数 2.请求乱码问题 3.参数绑注解@RequestParam 4.获得Restful风格的参数 5.自定义类型转换器 6.获得请求头 7.文件上传 8.小结 1.获得请求参数客户端请求参数的格式是:name=value&name=value- - 服务器端要获得请求的参数,有时还需要进行数据的封装,SpringMVC可以接收如下类型的参数: 1)基本类型
Java 超详细讲解十大排序算法面试无忧

目录排序算法的稳定性: 一.选择排序二.冒泡排序三.插入排序四.希尔排序五.堆排序六.归并排序七.快速排序八.鸽巢排序九.计数排序十.基数排序排序算法的稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,如果排序以后,保证这些记录的相对次序保持不变,即在原序列中,a[i]=a[j],且 a[i] 在 a[j] 之前,排序后保证 a[i] 仍在 a[j] 之前,则称这种排序算法是稳定的:否则称为不稳定的. 一.选择排序每次从待排序的元素中选择最小的元素,依次
Java超详细讲解类变量和类方法

目录 1.static静态变量 2.类变量(静态变量的访问) 3.类方法 1.static静态变量 1.静态变量被同一个类的所有对象共享 2.static类变量在类加载的时候就生成使用 static保存在class实例的尾部,在堆中 3.和C语言C++有点像 package com.demo.static_; import java.sql.SQLOutput; public class childgeme { public static void main(String[] args) { C
Java超详细讲解排序二叉树

目录排序二叉树概念排序二叉树类的定义添加节点中序遍历查找节点查找某一节点的父节点删除节点排序二叉树概念二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树.是数据结构中的一类. 对于二叉排序树的任何一个非叶子节点, 要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大. 对二叉排序树进行中序遍历,结果就是按从小到大排序的. 排序二叉树类的定义 public class binarySortTree {
Java 超详细讲解IO操作字节流与字符流

目录 IO操作字节流 FileInputStream FileOutputStream 字节流读写案例字符流 FileReader FileWriter 字节流与字符流的区别 IO操作字节流 java.io.InputStream 输入流,主要是用来读取文件内容的. java.io.OutputStream 输出流,主要是用来将内容字节写入文件的. FileInputStream 该流用于从文件读取数据,它的对象可以用关键字 new 来创建. 有多种构造方法可用来创建对象. 可以使用字符串
Java 超详细讲解类的定义方式和对象的实例化

目录 1.面对对象的初步认识 1.1什么是面向对象 1.2面向对象与面向过程 2.类的定义与使用 2.1简单认识类 2.2 类的定义格式 3.类的实例化 3.1什么是实例化? 3.2重点笔记总结 1.面对对象的初步认识 1.1什么是面向对象用面向对象的思想来涉及程序,更符合人们对事物的认知,对于大型程序的设计.扩展以及维护都非常友好. 1.2面向对象与面向过程举一个买手机的例子以面向对象的方式来处理买手机这件事的话,我们就不需要关注买手机的过程,具体手机怎么买,如何到手,用户不用去关心,