java图论弗洛伊德和迪杰斯特拉算法解决最短路径问题

目录

• 弗洛伊德算法
• 算法介绍
• 算法图解分析 
•  迪杰斯特拉算法
• 算法介绍
• 算法过程 

弗洛伊德算法

算法介绍

算法图解分析 

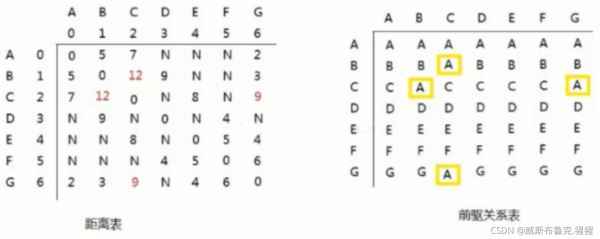
 第一轮循环中，以A(下标为：0)作为中间顶点

【即把作为中间顶点的所有情况都进行遍历，就会得到更新距离表和前驱关系】，距离表和前驱关系更新为：

弗洛伊德算法和迪杰斯特拉算法的最大区别是：

弗洛伊德算法是从各个顶点出发，求最短路径；

迪杰斯特拉算法是从某个顶点开始，求最短路径。

/**
	 * 弗洛伊德算法
	 * 容易理解，容易实现
	 */
	public void floyd() {
		int len = 0;//变量保存距离
		//对中间顶点遍历，k就是中间顶点的下标[A,B,C,D,E,F,G]
		for(int k = 0;k < dis.length;k++) {
			//从i顶点开始出发[A,B,C,D,E,F,G]
			for(int i = 0;i < dis.length;i++) {
				//到达j顶点 //[A,B,C,D,E,F,G]
				for(int j = 0;j < dis.length;j++) {
					len = dis[i][k] + dis[k][j];//=>求出从i顶点出发，经过k中间顶点，到达j顶点距离
					if(len < dis[i][j]) {//如果len小于dis[i][j]
						dis[i][j] = len;//更新距离
						pre[i][j] = pre[k][j];//更新前驱顶点
					}
				}
			}
		}
	}

 迪杰斯特拉算法

算法介绍

算法过程 

public class DijkstraAlgorithm {
	public static void main(String[] args) {
		char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
		// 邻接矩阵
		int[][] matrix = new int[vertex.length][vertex.length];
		final int N = 65535;// 表示不可以连接
		matrix[0] = new int[] { N, 5, 7, N, N, N, 2 };
		matrix[1] = new int[] { 5, N, N, 9, N, N, 3 };
		matrix[2] = new int[] { 7, N, N, N, 8, N, N };
		matrix[3] = new int[] { N, 9, N, N, N, 4, N };
		matrix[4] = new int[] { N, N, 8, N, N, 5, 4 };
		matrix[5] = new int[] { N, N, N, 4, 5, N, 6 };
		matrix[6] = new int[] { 2, 3, N, N, 4, 6, N };
		// 创建Graph对象
		Graph graph = new Graph(vertex, matrix);
		// 测试，图的邻接矩阵是否ok
		graph.showGraph();
		// 测试迪杰斯特拉算法
		graph.dsj(6);
		graph.showDijkstra();
	}
}
class Graph {
	private char[] vertex;// 顶点数组
	private int[][] matrix;// 邻接矩阵
	private VisitedVertex vv;// 已经访问过的顶点的集合
	// 构造器
	public Graph(char[] vertex, int[][] matrix) {
		this.vertex = vertex;
		this.matrix = matrix;
	}
	// 显示结果
	public void showDijkstra() {
		vv.show();
	}
	// 显示图
	public void showGraph() {
		for (int[] link : matrix) {
			System.out.println(Arrays.toString(link));
		}
	}
	/**
	 * 迪杰斯特拉算法实现
	 *
	 * @param index 表示出发顶点对应的下标
	 */
	public void dsj(int index) {
		vv = new VisitedVertex(vertex.length, index);
		update(index);// 更新index顶点到周围顶点的距离和前驱顶点
		for (int j = 1; j < vertex.length; j++) {
			index = vv.updateArr();// 选择并返回新的访问顶点
			update(index);// 更新index顶点到周围顶点的距离和前驱顶点
		}
	}
	/**
	 * 更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点
	 */
	private void update(int index) {
		int len = 0;
		// 根据遍历邻接矩阵的 matrix[index]行
		for (int j = 0; j < matrix[index].length; j++) {
			// len含义是：出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
			len = vv.getDis(index) + matrix[index][j];
			// 如果j顶点没有被访问过，并且len小于出发顶点到j顶点的距离，就需要更新
			if (!vv.in(j) && len < vv.getDis(j)) {
				vv.updateDis(j, index);// 更新j顶点的前驱为index顶点
				vv.updateDis(j, len);// 更新出发顶点到j顶点的距离
			}
		}
	}
}
//已访问顶点集合
class VisitedVertex {
	// 记录各个顶点是否访问过; 1表示访问过，0未访问，会动态更新
	public int[] already_arr;
	// 每个下标对应的值为前一个顶点下标，会动态更新
	public int[] pre_visited;
	// 记录出发顶点到其他所有顶点的距离，比如G为出发顶点，就会记录G到其他顶点的距离，动态更新，求的最短距离放到dis
	public int[] dis;
	/**
	 * 构造器
	 *
	 * @param length 表示顶点的个数
	 * @param index  出发顶点对应的下标，比如G顶点，下标就是6
	 */
	public VisitedVertex(int length, int index) {
		this.already_arr = new int[length];
		this.pre_visited = new int[length];
		this.dis = new int[length];
		// 初始化dis数组
		Arrays.fill(dis, 65535);
		this.already_arr[index] = 1;// 设置出发顶点被访问过
		this.dis[index] = 0;// 设置出发顶点的访问距离为0
	}
	/**
	 * 判断index顶点是否被访问过
	 *
	 * @param index
	 * @return 如果访问过，就返回true,否则返回false
	 */
	public boolean in(int index) {
		return already_arr[index] == 1;
	}
 	/**
	 * 更新出发顶点到index顶点的距离
	 *
	 * @param index
	 * @param len
	 */
	public void updateDis(int index, int len) {
		dis[index] = len;
	}
	/**
	 * 更新pre这个顶点的前驱顶点为index顶点
	 *
	 * @param pre
	 * @param index
	 */
	public void updatePre(int pre, int index) {
		pre_visited[pre] = index;
	}
	/**
	 * @return 返回出发顶点到index顶点的距离
	 */
	public int getDis(int index) {
		return dis[index];
	}
	public int updateArr() {
		int min = 65535, index = 0;
		for (int i = 0; i < already_arr.length; i++) {
			if (already_arr[i] == 0 && dis[i] < min) {
				min = dis[i];
				index = i;
			}
		}
		// 更新index顶点被访问过
		already_arr[index] = 1;
		return index;
	}
	// 显示最后的结果
	// 即将三个数组的情况输出
	public void show() {
		System.out.println("==========================");
		// 输出already_arr
		for (int i : already_arr) {
			System.out.print(i + " ");
		}
		// 输出pre_visited
		for (int i : pre_visited) {
			System.out.print(i + " ");
		}
		// 输出dis
		for (int i : dis) {
			System.out.print(i + " ");
		}
		System.out.println();
		// 为了好看最后的最短距离，如下处理
		char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
		int count = 0;
		for (int i : dis) {
			if (i != 65535) {
				System.out.print(vertex[count] + "(" + i + ")");
			} else {
				System.out.println("N");
			}
			count++;
		}
		System.out.println();
	}
}

以上就是java图论弗洛伊德和迪杰斯特拉算法解决最短路径问题的详细内容，更多关于弗洛伊德和迪杰斯特拉算法解决最短路径的资料请关注我们其它相关文章！