Python小波变换去噪的原理解析

一.小波去噪的原理

信号产生的小波系数含有信号的重要信息，将信号经小波分解后小波系数较大，噪声的小波系数较小，并且噪声的小波系数要小于信号的小波系数，通过选取一个合适的阀值，大于阀值的小波系数被认为是有信号产生的，应予以保留，小于阀值的则认为是噪声产生的，置为零从而达到去噪的目的。
小波阀值去噪的基本问题包括三个方面：小波基的选择，阀值的选择，阀值函数的选择。

(1) 小波基的选择：通常我们希望所选取的小波满足以下条件：正交性、高消失矩、紧支性、对称性或反对称性。但事实上具有上述性质的小波是不可能存在的，因为小波是对称或反对称的只有Haar小波，并且高消失矩与紧支性是一对矛盾，所以在应用的时候一般选取具有紧支的小波以及根据信号的特征来选取较为合适的小波。
(2) 阀值的选择：直接影响去噪效果的一个重要因素就是阀值的选取，不同的阀值选取将有不同的去噪效果。目前主要有通用阀值（VisuShrink）、SureShrink阀值、Minimax阀值、BayesShrink阀值等。
(3) 阀值函数的选择：阀值函数是修正小波系数的规则，不同的反之函数体现了不同的处理小波系数的策略。最常用的阀值函数有两种：一种是硬阀值函数，另一种是软阀值函数。还有一种介于软、硬阀值函数之间的Garrote函数。

另外，对于去噪效果好坏的评价，常用信号的信噪比（SNR）与估计信号同原始信号的均方根误差（RMSE）来判断。

二，在python中使用小波分析进行阈值去噪声,使用pywt.threshold函数

#coding=gbk
#使用小波分析进行阈值去噪声,使用pywt.threshold

import pywt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math 

data = np.linspace(1, 10, 10)
print(data)
# [ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]
# pywt.threshold(data, value, mode, substitute) mode 模式有4种，soft, hard, greater, less; substitute是替换值可以点进函数里看,data/np.abs(data) * np.maximum(np.abs(data) - value, 0)

data_soft = pywt.threshold(data=data, value=6, mode='soft', substitute=12)
print(data_soft)
# [12. 12. 12. 12. 12.  0.  1.  2.  3.  4.] 将小于6 的值设置为12， 大于等于6 的值全部减去6

data_hard = pywt.threshold(data=data, value=6, mode='hard', substitute=12)
print(data_hard)
# [12. 12. 12. 12. 12.  6.  7.  8.  9. 10.] 将小于6 的值设置为12， 其余的值不变

data_greater = pywt.threshold(data, 6, 'greater', 12)
print(data_greater)
# [12. 12. 12. 12. 12.  6.  7.  8.  9. 10.] 将小于6 的值设置为12，大于等于阈值的值不变化

data_less = pywt.threshold(data, 6, 'less', 12)
print(data_less)
# [ 1.  2.  3.  4.  5.  6. 12. 12. 12. 12.] 将大于6 的值设置为12， 小于等于阈值的值不变

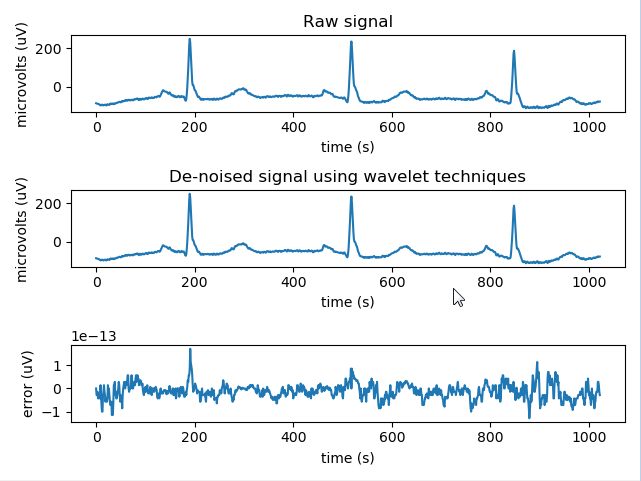三，在python中使用ecg心电信号进行小波去噪实验

#-*-coding:utf-8-*-

import matplotlib.pyplot as plt
import pywt
import math
import numpy as np

#get Data
ecg=pywt.data.ecg()  #生成心电信号
index=[]
data=[]
coffs=[]

for i in range(len(ecg)-1):
    X=float(i)
    Y=float(ecg[i])
    index.append(X)
    data.append(Y)
#create wavelet object and define parameters
w=pywt.Wavelet('db8')#选用Daubechies8小波
maxlev=pywt.dwt_max_level(len(data),w.dec_len)
print("maximum level is"+str(maxlev))
threshold=0  #Threshold for filtering

#Decompose into wavelet components,to the level selected:
coffs=pywt.wavedec(data,'db8',level=maxlev) #将信号进行小波分解

for i in range(1,len(coffs)):
    coffs[i]=pywt.threshold(coffs[i],threshold*max(coeffs[i]))

datarec=pywt.waverec(coffs,'db8')#将信号进行小波重构

mintime=0
maxtime=mintime+len(data)
print(mintime,maxtime)

plt.figure()
plt.subplot(3,1,1)
plt.plot(index[mintime:maxtime], data[mintime:maxtime])
plt.xlabel('time (s)')
plt.ylabel('microvolts (uV)')
plt.title("Raw signal")
plt.subplot(3, 1, 2)
plt.plot(index[mintime:maxtime], datarec[mintime:maxtime])
plt.xlabel('time (s)')
plt.ylabel('microvolts (uV)')
plt.title("De-noised signal using wavelet techniques")
plt.subplot(3, 1, 3)
plt.plot(index[mintime:maxtime],data[mintime:maxtime]-datarec[mintime:maxtime])
plt.xlabel('time (s)')
plt.ylabel('error (uV)')
plt.tight_layout()
plt.show()

到此这篇关于Python小波变换去噪的文章就介绍到这了,更多相关Python小波去噪内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！