C语言植物大战数据结构快速排序图文示例

目录

• 快速排序
• 一、经典1962年Hoare法
• 1.单趟排序
• 2.递归左半区间和右半区间
• 3.代码实现
• 二、填坑法(了解)
• 1.单趟思路
• 2.代码实现
• 三、双指针法(最佳方法)
• 1.单趟排序
• 2.具体思路
• 3.代码递归图
• 4.代码实现
• 四、三数取中优化(最终方案)
• 1.三数取中
• 2.代码实现(最终代码)
• 五、时间复杂度(重点)
• 1.最好情况下
• 2.最坏情况下
• 3.空间复杂度
• 六、非递归写法
• 1.栈模拟递归快排
• 2.队列实现快排
• 浅浅总结下

“田家少闲月，五月人倍忙”“夜来南风起，小麦覆陇黄”

C语言朱武大战数据结构专栏

C语言植物大战数据结构希尔排序算法

C语言植物大战数据结构堆排序图文示例

C语言植物大战数据结构二叉树递归

快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。所以快速排序有种方法是以他的名字命名的。相比70年前的祖师爷级的 大佬 来说，今天我们学习快速排序的成本已经非常低了。今天的我们的是站在巨人的肩膀上学习快速排序。

快速排序有三种方法实现，我们 都 需要掌握。

一、经典1962年Hoare法

让我们来看看1962年祖师爷发明的快排吧。

什么是快速排序？给你以下代码，请你完善快速排序，你将怎么完善？

快速排序：顾名思义，它比较快，整体而言适合各种场景下的排序。缺陷相较于其他排序小。且大部分 程序语言 排序的库函数 的 源代码都是由快速排序实现的

void QuickSort(int* a, int left, int right)
{
	//请你完善以下代码
}
int main()
{
	int arr[] = {6,1,2,7,9,3,4,5,10,8};
	int sz = sizeof(arr) / sizeof(arr[0]);
	QuickSort(arr, 0, sz-1);
	return 0;
}

具体实现：

Hoare法和二叉树的**前序遍历(根 左子树 右子树)**简直一模一样。

整体思路：

1.先进行一趟排序。

2.进行左半区间(左子树)递归。

3.进行右半区间(右子树)递归。

1.单趟排序

所有的排序的思想：就是先考虑单趟的排序，再合成n躺排序。这是毋庸置疑的，因为这样的思想很自然。

对于单趟排序，也有一个思路。可以说算是规定吧，这是祖师爷Hoare的规定。

为了好理解思路，以下思路是整体上的思路，写出来的程序还是有bug的。具体细节需要后期修改。

一定要按照规定走哦，不要问那么多为什么。按照规定走你就知道为什么要这么做了。总体思路规定：

1.设置一个基准值key，key一般为左边第一个数的下标。定义左指针left和有指针right分别指向第一个和最后一个。

2.先让右边的right指针往左走，一直找比key所指向小的数，找到后就停下。

3.紧接着让left指针往右走，一直找比key所指向大的数，找到后就停下。

4.如果第2步的right和第3步left都找到了，则交换swap两者的值。然后继续循环2和3步，直到left >= right为止。

5.此时left = right, 交换left和right相遇的位置的值 与 key位置上的值。

此时，Hoare 的单趟排序完成。产生的效果是key作为分割线，把大小分割开了，比key所指向值小的在key左边，比key所指向值大的在key右边。

2.递归左半区间和右半区间

对于单趟来说。

单趟排完之后，key已经放在正确的位置了。

如果左边有序，右边有序，那么我们整体就有序了。

那左边和右边如何有序呢？

解释：分治解决子问题。相当于二叉树。

一趟排序完成后，再对左半区间进行单趟排序，一直递归到什么时候结束呢？

解释：递归到左半区间只有一个值的时候，或者为空的时候递归结束。

这个过程适合用 画递归图 来查看。

由于数据是10个数，递归图庞大。所以此处省略。下面双指针法有具体递归图。

3.代码实现

具体代码实现和你想的总是那么不同。因为特殊情况确实是存在，且还是那么离谱。

我认为这个题难在了边界问题，边界问题要时刻注意！。

特殊情况1：当排以下数据时，我只是把6改了，这样会导致right和left直接不走了。

{6,1,2,7,9,3,4,5,10,6}

特殊情况2：当排以下数据时，会发生left找不到最大的值导致越界。

{5,4,3,2,1}

改动如下。

//快速排序Hoare
int PartSort(int* a, int left,int right)
{
	int key = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[key])
		{
			--right;
		}
		while (left < right && a[left] <= a[key])
		{
			++left;
		}
		swap(&a[left], &a[right]);
	}
	swap(&a[left], &a[key]);
	return left;
}
void QuickSort(int* a, int left, int right)
{
	//当有个区间为空的时候right-left会小于0。
	if (right <= left)
		return;
	int div = PartSort(a, left, right);
	QuickSort(a, left, div-1);
	QuickSort(a, div+1, right);
}
int main()
{
	int arr[] = {6,1,2,7,9,3,4,5,10,8};
	int sz = sizeof(arr) / sizeof(arr[0]);
	QuickSort(arr, 0, sz-1);
	return 0;
}

二、填坑法(了解)

和Hoare法思想类似，大差不差，没什么区别。相比Hoare法较好理解。因为挖坑填坑思想很生动形象，所以较好理解。

1.单趟思路

单趟思路：

1.先保存key的值。让左边的key做坑(pit)，让右边找比key小的，然后填到坑中。

2.然后让那个小的做坑，再让左边找比key大的，找到后填到坑中。依次循环，直到right和left相遇。

3.相遇后，把key的值填到相遇的位置。

这时，单趟循环结束。

2.代码实现

和Hoare法相似，只是少了交换的步骤。注意：要事先把key的值保存下来。

int PartSort(int* a, int left, int right)
{
	int keyval = a[left];
	int pit = left;
	while (left < right)
	{
		while (left < right && a[right] >= keyval)
		{
			right--;
		}
		a[pit] = a[right];
		pit = right;
		while (left < right && a[left] <= keyval)
		{
			left++;
		}
		a[pit] = a[left];
		pit = left;
	}
	a[pit] = keyval;
	return left;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int div = PartSort(a, left, right);
	QuickSort(a, left, div - 1);
	QuickSort(a, div + 1, right);
}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	QuickSort(arr, 0, sz-1);
	return 0;
}

三、双指针法(最佳方法)

1.单趟排序

和以上两种方法的不同之处只有单趟排序，也就是PartSort函数的部分.

优点：有了双指针的优化，不需要考虑 边界问题！写代码不易出错。

代码好写，不好理解。代码极为简单，只需五行。

双指针法也称快慢指针法，两个指针一前一后

2.具体思路

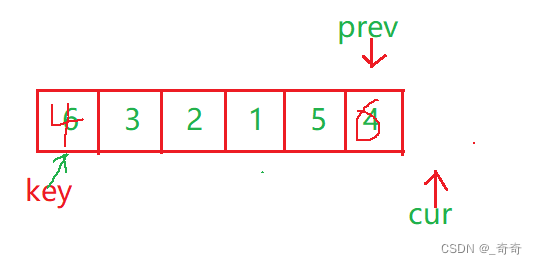
对于排6,3,2,1,5,4的升序来说。

思路：让cur找比key指向的值小的，找到后，++prev，交换prev和cur位置的值。若cur比key指向的值大，则不交换。

prev和cur的关系：

1.cur还没遇到比key大的值时，prev紧跟着cur，一前一后。

2.cur遇到比key大的，prev和cur之间的一段都是最大的值

第一趟排序后的结果。这时候div为基准值。将左右子树分隔开。

全部排完序后的二叉树图。

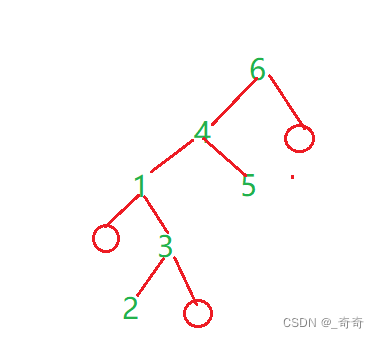
3.代码递归图

红色线代表递归，绿色线代表返回。

4.代码实现

#include <stdio.h>
void Swap(int* x, int* y)
{
	int t = 0;
	t = *x;
	*x = *y;
	*y = t;
}
int PartSort(int* a, int left, int right)
{
	int key = left;
	int prev = left;
	int cur = left + 1;
	//推荐写法一，较好理解
	while (cur <= right)
	{
		if (a[cur] < a[key])
		{
			++prev;
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	//写法二。比较妙，不好理解
	//while (cur <= right)
	//{
	//	if (a[cur] < a[key] && a[++prev] != a[cur])
	//	{
	//		Swap(&a[cur], &a[prev]);
	//	}
	//	++cur;
	//}
	Swap(&a[prev], &a[key]);
	return prev;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int div = PartSort(a, left, right);
	QuickSort(a, left, div - 1);
	QuickSort(a, div + 1, right);
}
int main()
{
	int arr[] = {6,3,2,1,5,4};
	int sz = sizeof(arr) / sizeof(arr[0]);
	QuickSort(arr, 0, sz-1);
	return 0;
}

到这里快速排序还没有完，因为它存在缺陷。还需继续优化。请往下看

四、三数取中优化(最终方案)

以上三种方法的时间复杂度

最好情况：是O(N*Log2N)。

最坏情况：也就是在数据有序的情况下，就退化为了冒泡排序 O(N2)

当给你一组上万个数据测试时，会发生超时现象。

例如LeetCode912. 排序数组

快排竟然超时了，这时候用三数取中来解决此问题。

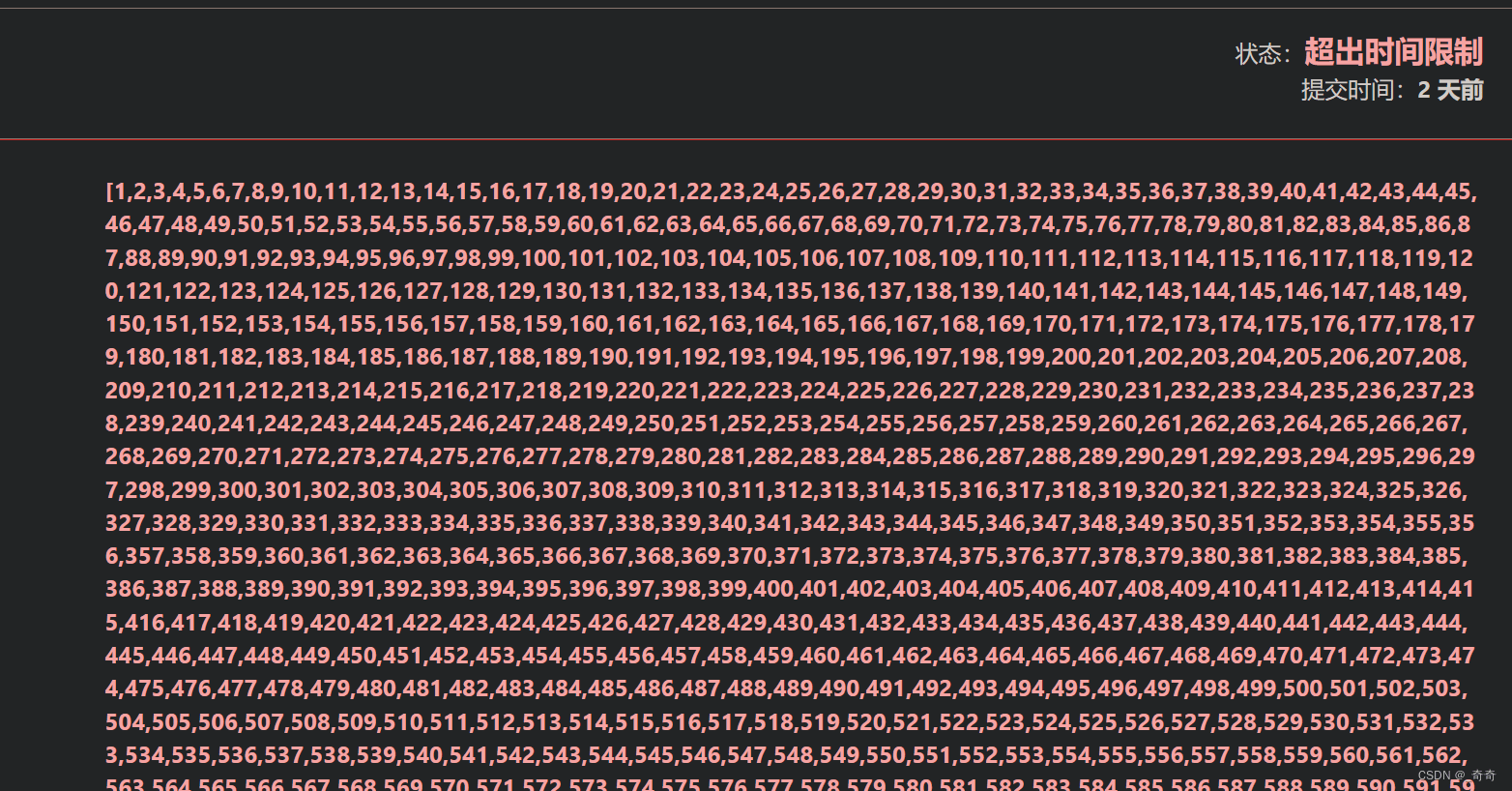
1.三数取中

三数取中的含义：取三个数中间不是最大也不是最小的那个。哪三个数？第一个，最后一个，和中间那个。例如排以下数据时。

9 8 7 6 5 4 3 2 1 0

思路：

默认key选最左边的数。

1.三个数取第一个 9 和第二个 1 和中间的 5

2.选出不是最大也不是最小的那个，也就是5。

3.将5和key交换位置。也就是和最左边的数交换。

这样做可以打破单边树形状，可以使之变为二分。因为这时候5做了key，key的左边是比5小的，

key的右边是比key大的。

二分后的时间复杂度还是N*LogN

注意：三数取中仍然无法完全解决

在某种特殊情况序列下时间复杂度变为O(n2)的情况

2.代码实现(最终代码)

int GetMidIndex(int* a, int left, int right)
{
	//防溢出写法
	//int mid = left + (right - left) / 2;
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[right] > a[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
int PartSort(int* a, int left, int right)
{
	int midi = GetMidIndex(a, left, right);
	Swap(&a[midi], &a[left]);
	int key = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < a[key])
		{
			++prev;
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	Swap(&a[prev], &a[key]);
	return prev;
}
void QuickSort(int* a, int left, int right)
{
	if (right <= left)
		return;
	int div = PartSort(a, left, right);
	QuickSort(a, left, div - 1);
	QuickSort(a, div + 1, right);
}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	QuickSort(arr, 0, sz-1);
	return 0;
}

五、时间复杂度(重点)

结论大家都会，是N*LogN。怎么算出来的呢？

1.最好情况下

在最好的情况下：每次选key刚好能平分这组数据，一直都是二分，构成了满二叉树。

1.对于单趟排序的一层递归，不管是哪种方法，left和right每次都遍历了一遍数组，时间复杂度为N。

2.因为满二叉树的高度为Log2N，所以递归深度(深度不等于次数)也为Log2N，所以递归Log2N层就是(N *Log2N).

3.综上所述，快排最好情况下时间复杂度为O(N * LogN).

2.最坏情况下

最坏情况下，每次选key都是最大或者最小的那个元素，这使得每次划分所得的子表中一个为空表，另一个表的长度为原表的长度-1.

这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法退化为冒泡排序，时间复杂度为N2

如图是给9 8 7 6 5 4 3 2 1排升序的例子。

每次选最左边的为key。

3.空间复杂度

在空间上来看，尽管快排只需要一个元素的辅助空间。

但是快排需要一个栈空间来实现递归

最好情况下：每一次都被均匀的分割为深度相近的两个子表，所需要栈的最大深度为Log2N。空间复杂度为O(Log2N)

最坏情况下：但最坏的情况下，栈的最大深度为n.这样快速排序的空间复杂度为O(N).这时就会导致栈溢出(Stack Overflow)。因为栈的空间很小。

这时候就需要非递归的算法，来解决栈溢出问题。

六、非递归写法

1.栈模拟递归快排

如图对以下数据排序

{ 6,1,2,7,9,3,4,5,10,8 }

void QuickSort(int* a, int begin, int end)
{
	ST st;
	StackInit(&st);
	//先入0和9这段区间
	StackPush(&st, begin);
	StackPush(&st, end);
	while (!StackEmpty(&st))
	{
		//接着出栈，9和0，注意后进先出
		int end = StackTop(&st);
		StackPop(&st);
		int begin = StackTop(&st);
		StackPop(&st);
		//然后再进行对0和9这段区间单趟排序。
		int keyi = PartSort(a, begin, end);
		//[begin , keyi - 1] [keyi+1,end]
		//最后判断区间是否为最小规模子问题，来判断是否需要继续入栈。
		if (begin < keyi - 1)
		{
			StackPush(&st, begin);
			StackPush(&st, keyi - 1);
		}
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, end);
		}
	}
	//记得销毁栈。
	StackDestory(&st);
}

由此可以看出，虽然栈实现快排不是递归，但是和递归的思想一样。简直和递归一模一样。

2.队列实现快排

废话不多说。看图

//快速排序的非递归形式1：通过队列来实现
void QuickSort(int* a, int begin, int end)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, begin);
	QueuePush(&q, end);
	while (!QueueEmpty(&q))
	{
		int left = QueueFront(&q);
		QueuePop(&q);
		int right = QueueFront(&q);
		QueuePop(&q);
		int keyi = PartSort(a, left, end);//[left,keyi-1][keyi+1,right]
		if (left < keyi - 1)
		{
			QueuePush(&q, left);
			QueuePush(&q, keyi - 1);
		}
		if (keyi + 1 < right)
		{
			QueuePush(&q, keyi + 1);
			QueuePush(&q, right);
		}
	}
	QueueDestory(&q);
}

浅浅总结下

快排的平均时间复杂度为O(N*LogN)

如果每次划分只有一半区间，另一半区间为空，则时间复杂度为n2

快排对初始顺序影响较大，假如数据有序时，其性能最差。对初始顺序比较敏感

以上就是C语言植物大战数据结构快速排序图文示例的详细内容，更多关于C语言数据结构快速排序的资料请关注我们其它相关文章！