C#数据类型实现背包、队列和栈
目录
- 基础编程模型和数据抽象
- 1. API
- 1. 背包
- 2.先进先出队列
- 3. 下压栈
- 2.用数组实现
- 3.链表
- 1.构造链表
- 2.在表头插入结点
- 3.从表头删除结点
- 4.在表尾插入结点
- 5.其他位置的插入和删除操作
- 6. 遍历
- 4. 用链表实现背包
- 5. 用链表实现栈
- 6. 用链表实现队列
- 7. 总结
基础编程模型和数据抽象
把描述和实现算法所用到的语言特性,软件库和操作系统特性总称为基础编程模型。
编写递归代码注意的点:
- 1. 递归总有一个最简单的情况 —— 方法的第一条语句总是包含 return 的条件语句。
- 2. 递归调用总是尝试解决一个规模更小的子问题,这样递归才能收敛到最简单的情况。
- 3. 递归调用的父问题和尝试解决的子问题之间不应该有交集。
数据类型指的是一组值和一组对这些值的操作的集合。抽象数据类型(ADT) 是一种能够对使用者隐藏数据表示的数据类型。用高级语言的类来实现抽象数据类型和用一组静态方法实现一个函数库并没有什么不同。抽象数据类型的主要不同之处在于它将数据和函数的实现关联,并将数据的表示方式隐藏起来。在使用抽象数据类型时,我们的注意力集中在API 描述的操作上而不会去关心数据的表示;在实现抽象数据类型时,我们的注意力集中在数据本身并将实现对该数据的各种操作。
抽象数据之所以重要是因为在程序设计上支持封装。
我们研究同一问题的不同算法的主要原因在于他们的性能特点不同。抽象数据类型可以在不修改测试代码的情况下用一种算法替换另一种算法。
数据抽象中的一个基础概念:对象是能够承载数据类型的值的实体。所有的对象都有三大特性:状态,标识和行为。对象的状态即数据类型中的值。对象的标识就是它在内存中的位置。对象的行为就是数据类型的操作。
许多基础数据类型都和对象的集合有关。数据类型的值就是一组对象的集合,所有操作都是关于添加,删除或是访问集合中的对象。背包(Bag),队列(Quene)和栈(Stack) 它们的不同之处在于删除或者访问对象的顺序不同。
1. API

Stack 和 Quene 都含有一个能够删除集合中特定元素的方法。
实现上面API需要高级语言的特性:泛型,装箱拆箱,可迭代(实现IEnumerable 接口)。
1. 背包
背包是一种不支持从中删除元素的集合类型——它的目的就是帮助用例收集元素并迭代遍历所有元素。用例也可以使用栈或者队列,但使用 Bag 可以说明元素的处理顺序不重要。
2.先进先出队列
队列是基于先进先出(FIFO)策略的集合类型。
3. 下压栈
下压栈(简称栈)是一种基于后进先出(LIFO)策略的集合类型。
应用例子:计算输入字符串 (1+((2+3)*(4*5)))表达式的值。
使用双栈解决:
- 1. 将操作数压入操作数栈;
- 2. 将运算符压入运算符栈;
- 3. 忽略做括号;
- 4. 在遇到右括号时,弹出一个运算符,弹出所需数量的操作数,并将运算符和操作数的运算结果压入操作数栈。
2.用数组实现
实现下压栈:
//想要数据类型可迭代,需要实现IEnumerable
public class ResizingStack<Item> : IEnumerable<Item>
{
private Item[] a = new Item[1];
private int N = 0;
public bool IsEmpty{ get {
return N == 0;
} }
public int Size { get {
return N;
} }
public int Count { get; set; }
/// <summary>
/// 使数组处于半满
/// </summary>
/// <param name="max"></param>
private void Resize(int max)
{
Count = 0;
Item[] temp = new Item[max];
for(var i = 0;i<N;i++)
{
temp[i] = a[i];
Count++;
}
a = temp;
}
public void push(Item item)
{
if (N == a.Length)
Resize(a.Length * 2);
a[N++] = item;
}
public Item Pop()
{
Item item = a[--N];
a[N] = default(Item); //避免对象游离
if (N > 0 && N == a.Length / 4)
Resize(a.Length/2);
return item;
}
IEnumerator<Item> IEnumerable<Item>.GetEnumerator()
{
return new ResizingStackEnumerator<Item>(a);
}
public IEnumerator GetEnumerator()
{
return new ResizingStackEnumerator<Item>(a);
}
}
class ResizingStackEnumerator<Item> : IEnumerator<Item>
{
private Item[] a;
private int N = 0;
public ResizingStackEnumerator(Item[] _a)
{
a = _a;
N = a.Length-1;
}
public object Current => a[N--];
Item IEnumerator<Item>.Current => a[N--];
public void Dispose()
{
throw new NotImplementedException();
}
public bool MoveNext()
{
return N > 0;
}
public void Reset()
{
throw new NotImplementedException();
}
}
3.链表
链表是在集合类的抽象数据类型实现中表示数据的另一种基础数据结构。
定义:链表是一种递归的数据结构,它或者指向空,或者指向另一个节点的引用,该节点含有一个泛型元素和一个指向另一个链表的引用。
class Node<Item>
{
public Item item { get; set; }
public Node<Item> Next { get; set; }
}
1.构造链表
链表表示的是一列元素。
根据递归的定义,只需要一个 Node 类型的变量就能表示一条链表,只要保证它的 Next 值是 null 或指向另一个 Node 对象,该对象的 Next 指向另一条链表。

2.在表头插入结点
在链表列表中插入新节点的最简单位置是开始。要在首结点为 first 的给定链表开头插入字符串 not ,先将 first 保存在 oldfirst 中,然后将一个新结点赋予 first ,并将 first 的 item 设为 not, Next 设置为 oldfirst 。
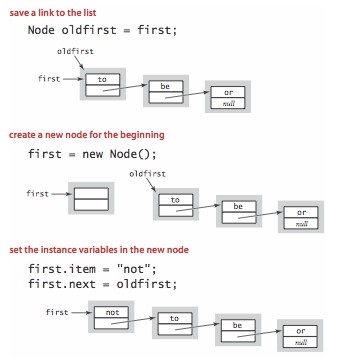
在链表开头插入一个结点所需的时间和链表长度无关。
3.从表头删除结点
只需将 first 指向 first.next 即可。first 原来指向的对象变成了一个孤儿,垃圾回收机制会将其回收。

同样,该操作所需的时间和链表长度无关。
4.在表尾插入结点
当链表不止有一个结点时,需要一个指向链表最后结点的链接 oldlast,创建新的结点,last 指向新的最后结点。然后 oldlast.next 指向 last。

当链表只有一个结点时,首结点又是尾结点。只需将 last 指向新的结点,然后 first.next 指向 last。
5.其他位置的插入和删除操作
上述操作可以很容易的实现,但是下面的操作比较复杂:
- 1. 删除指定的结点
- 2. 在指定结点前插入一个新结点
这些操作需要我们遍历链表,它所需的时间和链表的长度成正比。想要实现任意插入和删除结点需要使用双向链表,其中每个结点都含有两个链接,分别指向上一个和下一个结点。
6. 遍历
简单实现:
public class Bag<Item>
{
private Node<Item> first;
public void Add(Item item)
{
Node<Item> oldFirst = first;
first = new Node<Item>() {
item = item,
Next = oldFirst
};
}
}
Bag<int> bags = new Bag<int>();
for (var i = 0; i < 10; i++)
{
bags.Add(i);
}
for (var x = bags.first; x != null; x = x.Next)
{
Console.WriteLine(x.item);
}
实现 IEnumerable 接口 实现遍历:
public class Bag<Item>: IEnumerable<Item>
{
public Node<Item> first;
public void Add(Item item)
{
Node<Item> oldFirst = first;
first = new Node<Item>() {
item = item,
Next = oldFirst
};
}
public IEnumerator<Item> GetEnumerator()
{
return new LineEnumerator<Item>(first);
}
IEnumerator IEnumerable.GetEnumerator()
{
return new LineEnumerator<Item>(first);
}
}
public class LineEnumerator<Item> : IEnumerator<Item>
{
public Node<Item> first;
public LineEnumerator(Node<Item> _first)
{
first = _first;
}
public Item Current { get {
var oldfirst = first;
first = first.Next;
return oldfirst.item;
} }
object IEnumerator.Current => first;
public void Dispose()
{
return;
}
public bool MoveNext()
{
if (first != null)
return true;
return false;
}
public void Reset()
{
throw new NotImplementedException();
}
}
public static void LineTest()
{
Bag<int> bags = new Bag<int>();
for (var i = 0; i < 10; i++)
{
bags.Add(i);
}
foreach(var bag in bags)
{
Console.WriteLine(bag);
}
}
4. 用链表实现背包
见上述代码。
5. 用链表实现栈
Stack API 中 Pop() 删除一个元素,按照前面的从表头删除结点实现,Push() 添加一个元素,按照前面在表头插入结点。
public class Stack<Item> : IEnumerable<Item>
{
public Node<Item> first;
private int N;
public bool IsEmpty()
{
return first == null; //或 N == 0
}
public int Size()
{
return N;
}
public void Push(Item item)
{
Node<Item> oldfirst = first;
first = new Node<Item>() {
item = item,
Next = oldfirst
};
N++;
}
public Item Pop()
{
Item item = first.item;
first = first.Next;
N--;
return item;
}
public IEnumerator<Item> GetEnumerator()
{
return new StackLineIEnumerator<Item>(first);
}
IEnumerator IEnumerable.GetEnumerator()
{
return new StackLineIEnumerator<Item>(first);
}
}
public class StackLineIEnumerator<Item> : IEnumerator<Item>
{
private Node<Item> first;
public StackLineIEnumerator(Node<Item> _first)
{
first = _first;
}
public Item Current { get {
var oldfirst = first;
first = first.Next;
return oldfirst.item;
} }
object IEnumerator.Current => throw new NotImplementedException();
public void Dispose()
{
return;
}
public bool MoveNext()
{
return first != null;
}
public void Reset()
{
throw new NotImplementedException();
}
}
链表的使用达到了最优设计目标:
- 1. 可以处理任意类型的数据;
- 2. 所需的空间总是和集合的大小成正比;
- 3. 操作所需的时间总是和集合的大小无关;
6. 用链表实现队列
需要两个实例变量,first 指向队列的开头,last 指向队列的表尾。添加一个元素 Enquene() ,将结点添加到表尾(链表为空时,first 和 last 都指向新结点)。删除一个元素 Dequene() ,删除表头的结点(删除后,当队列为空时,将 last 更新为 null)。
public class Quene<Item> : IEnumerable<Item>
{
public Node<Item> first;
public Node<Item> last;
private int N;
public bool IsEmpty()
{
return first == null;
}
public int Size()
{
return N;
}
public void Enquene(Item item)
{
var oldlast = last;
last = new Node<Item>() {
item = item,
Next = null
};
if (IsEmpty())
first = last;
else
oldlast.Next = last;
N++;
}
public Item Dequene()
{
if (IsEmpty())
throw new Exception();
Item item = first.item;
first = first.Next;
if (IsEmpty())
last = null;
N--;
return item;
}
public IEnumerator<Item> GetEnumerator()
{
return new QueneLineEnumerator<Item>(first);
}
IEnumerator IEnumerable.GetEnumerator()
{
return new QueneLineEnumerator<Item>(first);
}
}
public class QueneLineEnumerator<Item> : IEnumerator<Item>
{
private Node<Item> first;
public QueneLineEnumerator(Node<Item> _first)
{
first = _first;
}
public Item Current { get {
var oldfirst = first;
first = first.Next;
return oldfirst.item;
} }
object IEnumerator.Current => throw new NotImplementedException();
public void Dispose()
{
return;
}
public bool MoveNext()
{
return first != null ;
}
public void Reset()
{
throw new NotImplementedException();
}
}
7. 总结
在结构化存储数据集时,链表是数组的一种重要的替代方式。
数组和链表这两种数据类型为研究算法和更高级的数据结构打下了基础。
基础数据结构:
| 数据结构 | 优点 | 缺点 |
|---|---|---|
| 数组 | 通过索引可以直接访问任意元素 | 在初始化时就需要知道元素的数量 |
| 链表 | 使用的空间大小和元素数量成正比 | 需要通过引用访问任意元素 |
在研究一个新的应用领域时,可以按照以下步骤识别目标,定义问题和使用数据抽象解决问题:
- 1. 定义 API
- 2. 根据特定的应用场景开发用例代码
- 3. 描述一种数据结构(即一组值的表示),并在 API 的实现中根据它定义类的实例变量。
- 4. 描述算法,即实现 API,并根据它应用于用例
- 5. 分析算法的性能
到此这篇关于C#数据类型实现背包、队列和栈的文章就介绍到这了。希望对大家的学习有所帮助,也希望大家多多支持我们。

