C语言植物大战数据结构二叉树递归
目录
- 前言
- 一、二叉树的遍历算法
- 1.构造二叉树
- 2.前序遍历(递归图是重点.)
- 3.中序遍历
- 4.后序遍历
- 二、二叉树遍历算法的应用
- 1.求节点个数
- 3.求第k层节点个数
- 4.查找值为x的节点
- 5.二叉树销毁
- 6.前序遍历构建二叉树
- 7.判断二叉树是否是完全二叉树
- 8.求二叉树的深度
- 三、二叉树LeetCode题目
- 1.单值二叉树
- 2. 检查两颗树是否相同
- 3. 对称二叉树
- 4.另一颗树的子树
- 6.反转二叉树
" 梧桐更兼细雨,到黄昏、点点滴滴。"
C语言朱武大战数据结构专栏
C语言植物大战数据结构快速排序图文示例
C语言植物大战数据结构希尔排序算法
C语言植物大战数据结构堆排序图文示例
前言
本篇用C语言递归来实现二叉树的基本操作。主要用到分治思想
1.本篇文章和代码旨在用于链式二叉树基本操作的复习。主要是递归的应用。
2.深刻理解二叉树是递归定义的这一概念。
分治递归思想:
1.把大问题分割为不可再分割的子问题。。
2.然后一步一步的返回
一、二叉树的遍历算法
二叉树的精髓在于遍历。遍历掌握了后,剩下的问题迎刃而解。
1.构造二叉树
“工欲善其事必利其器”
1.所以先创建一个结构体。
2.手动先构造一颗如图所示的二叉树。
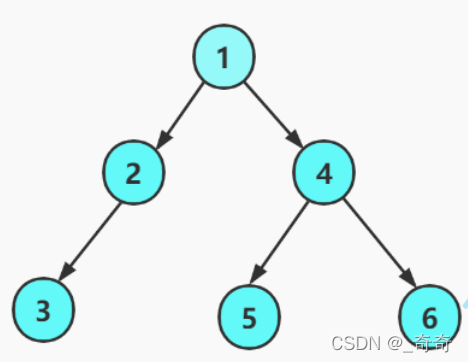
typedef int BTDataType;//定义二叉树结构体typedef struct BinaryTreeNode{<!--{C}%3C!%2D%2D%20%2D%2D%3E-->int data;//节点数据struct BinartTreeNode* left;//左子树struct BinartTreeNode* right;//右子树}BTNode;//构造一棵二叉树BTNode* BuyBTNode(BTDataType x){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->printf("malloc fail\n");exit(-1);}node->data = x;node->left = NULL;node->right = NULL;return node;}BTNode* CreatBinaryTree(){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->BTNode* node1 = BuyBTNode(1);BTNode* node2 = BuyBTNode(2);BTNode* node3 = BuyBTNode(3);BTNode* node4 = BuyBTNode(4);BTNode* node5 = BuyBTNode(5);BTNode* node6 = BuyBTNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;}int main(){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->BTNode* tree = CreatBinaryTree();return 0;}typedef int BTDataType;
//定义二叉树结构体
typedef struct BinaryTreeNode
{
int data;//节点数据
struct BinartTreeNode* left;//左子树
struct BinartTreeNode* right;//右子树
}BTNode;
//构造一棵二叉树
BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
printf("malloc fail\n");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyBTNode(1);
BTNode* node2 = BuyBTNode(2);
BTNode* node3 = BuyBTNode(3);
BTNode* node4 = BuyBTNode(4);
BTNode* node5 = BuyBTNode(5);
BTNode* node6 = BuyBTNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
int main()
{
BTNode* tree = CreatBinaryTree();
return 0;
}
2.前序遍历(递归图是重点.)

遍历顺序:根 左子树 右子树
思路:
1.把每个节点都想成是一棵树。
2.当树为空时。
3.当树不为空时,先遍历左子树,后遍历右子树
注意:前中后序遍历不同处只在printf打印的顺序的位置。
// 二叉树前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
//打印在前
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
打印结果:
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
递归分析图:
递归题目的万能的解法。就是画递归图。
二叉树的所有题目,假如你不会,赶快 画递归图 吧
由于递归太庞大,图片太小看不清,所以我把左子树和右子树分开又截了图
1.红线部分代表压栈递归。
2.绿线部分代表 返回

左子树

右子树

3.中序遍历
遍历顺序:左子树 根 右子树
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
//打印在中间
printf("%d ", root->data);
InOrder(root->right);
}
打印结果
NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
4.后序遍历
遍历顺序:左子树 右子树 根
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
//打印在最后
printf("%d ", root->data);
}
打印结果
NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
5.层序遍历
思路:
借助先进先出的性质,上一层节点出的时候,带下一层的节点进去。
1.先把根入队列。
2.根节点出来的时候,左右孩子进去。
// 层序遍历
void LevelOrder(BTNode* root)
{
//初始化队列,注意队列里面存的是 指针类型。
Queue q;
QueueInit(&q);
//如果树不为空开始入队
if (root)
{
QueuePush(&q, root);
}
//树不为空开始出对头数据,同时入队左子树和右子树,直到队列为空。
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
//如果还有左右子树,继续入队,否则不入队
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
//记得销毁队列
printf("\n");
QueueDestory(&q);
}
二、二叉树遍历算法的应用
1.求节点个数
思想:把大问题逐步分割为子问题。
思路:
1.树为空时返回0个节点。(树为空不意味着才开始就是空树,而是递归到最后一个为NULL的树返回)
2.树不为空时返回自己的1个节点+上一颗树返回的节点的个数。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
//当树为空时
if (root == NULL)
return 0;
//当树不为空时
return BinaryTreeSize(root->left) +
BinaryTreeSize(root->right) + 1;
}
2.求叶子节点个数
思路:
1.树为NULL时,返回0.
2.两颗子树都不为NULL时,返回1.
3.不满足以上两种情况,继续递归左右子树。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
//当树为空时
if (root == NULL)
return 0;
//当两棵 子 树都为空时
if (root->left == NULL && root->right == NULL)
return 1;
/*程序都到这一行, 意味着树不满足返回的情况,
所以继续递归 左子树和 右子树。*/
return BinaryTreeLeafSize(root->left)+
BinaryTreeLeafSize(root->right);
}
3.求第k层节点个数

思想:求上图第3层节点个数。
1.站在第1层来看,就是求第3层节点的个数
2.站在第2层的角度来看,就是求第2层节点的个数
3.站在第3层的角度来看,就是求第1层节点的个数
思路:
1.当树为空时返回0
2.当k为1时返回1。
3.不满足1和2,继续递归左右子树。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
//当树为空时
if (root == NULL)
return 0;
//当k为1时
if (k == 1)
return 1;
//程序能走到这一行,说明树不为空,k也不为1.继续递归
return BinaryTreeLevelKSize(root->left, k-1)+
BinaryTreeLevelKSize(root->right, k - 1);
}
4.查找值为x的节点
思想:
1.把最小规模的问题写在最前面作为限制
2.不满足最小规模的问题,则继续递归。将问题一步一步拆分为不可分割的子问题。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
//当树为空时
if (root == NULL)
return NULL;
//当树的值等于x时
if (root->data == x)
return root;
/*走到这一行,说明不满足以上条件。
开始递归左右子树,如果找到了,直接一步一步往回返*/
BTNode* a = BinaryTreeFind(root->left, x);
if (a)
{
return a;
}
BTNode* b = BinaryTreeFind(root->right, x);
if (b)
{
return b;
}
//没有x,则返回空
return NULL;
}
5.二叉树销毁
思路:相当于二叉树的后序遍历。
先把左右子树遍历完后,开始遍历根,对根进行free。
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
//free掉根
free(root);
}
6.前序遍历构建二叉树
思路:
对一串字符进行先序遍历,递归遍历二叉树,当遇见#时开始返回 连接 树。

通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
#include <stdio.h>
#include <stdlib.h>
typedef struct BTNodeTree
{
struct BTNodeTree* left;
struct BTNodeTree* right;
char val;
}BTNode;
//创建二叉树
BTNode* CreateTree(char* a, int* pi)
{
//如果树为#则返回null
if(a[*pi] == '#')
{
(*pi)++;
return NULL;
}
//否则构建节点,同时让pi++,以便继续递归
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->val = a[(*pi)++];
//构建左右子树
root->left = CreateTree(a, pi);
root->right = CreateTree(a, pi);
//构建完后返回根节点。
return root;
}
//中序遍历打印。
void inorder(BTNode* root)
{
if(root == NULL)
return;
inorder(root->left);
printf("%c ", root->val);
inorder(root->right);
}
int main()
{
char a[100];
scanf("%s", a);
int i = 0;
BTNode* tree = CreateTree(a, &i);
inorder(tree);
return 0;
}
7.判断二叉树是否是完全二叉树
思路:
1.层序遍历,空节点也进队列
2.出到空节点以后,出队列中所有数据,如果全是空,则是完全二叉树
8.求二叉树的深度
思路:二叉树的最大深度等价于:左右子树的最大深度 + 1
int maxDepth(struct TreeNode* root)
{
if(root == NULL)
{
return 0;
}
size_t left = maxDepth(root->left) + 1;
size_t right = maxDepth(root->right) + 1;
if(right > left)
{
return right;
}
return left;
}
//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//空后面出到非空,那说明不是完全二叉树
if (front)
return false;
}
//否则是完全二叉树
return true;
}
三、二叉树LeetCode题目
以下题目均属于LeetCode的 简单 题目
1.单值二叉树

如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
思想:
1.看一棵树的三个部分是否相同,相同则继续递归下一颗树,直到树为空。
bool isUnivalTree(struct TreeNode* root)
{
//当树为空时。
if(root == NULL)
{
return true;
}
//当右树不为空,并且 根 != 左树
//当右树不为空,并且 根 != 右树时
if(root->left != NULL && root->val != root->left->val)
return false;
if(root->right != NULL && root->val != root->right->val)
return false;
//能走到这一行,说明第一层树的值相同了。接着递归左右子树。
return isUnivalTree(root->left) &&
isUnivalTree(root->right);
}
2. 检查两颗树是否相同


给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//当两树都为空时
if(p == NULL && q== NULL)
return true;
//当其中一个树为空时
if(p == NULL || q == NULL)
return false;
//走到这里说明两树存在,比较两树的值
if(p->val != q->val)
return false;
//走到这里说明两树的根节点相同,继续递归,直到判断完左右子树为止。
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}
3. 对称二叉树

给你一个二叉树的根节点 root , 检查它是否轴对称。
bool isSym(struct TreeNode* q, struct TreeNode* p)
{
//当只有一个根节点时
if(q == NULL && p == NULL)
return true;
//当其中一个子树为空时
if(q == NULL ||p ==NULL)
return false;
//程序走到一这行,说明左右节点存在。当两个根节点不相等时
if(q->val != p->val)
return false;
//走到这一步说明左右节点相同,开始递归左右子树
return isSym(q->left, p->right) && isSym(q->right, p->left);
}
bool isSymmetric(struct TreeNode* root)
{
//当是空树时
if(root == NULL)
return true;
return isSym(root->left, root->right);
}
4.另一颗树的子树



思路:
用到了上一题判断两棵树是否相同的思想。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//当两树都为空时
if(p == NULL && q== NULL)
return true;
//当其中一个树为空时
if(p == NULL || q == NULL)
return false;
//走到这里说明两树存在,比较两树的值
if(p->val != q->val)
return false;
//走到这里说明两树的根节点相同,继续递归
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
//递归结束条件。当根为空时,并不是说明没有节点,可能是所有的子树都遍历过了。然后不相等返回false
if(root == NULL)
return false;
//走到这里说明子树不为空,开始比较子树和sub相同不。
bool a = isSameTree(root, subRoot);
if(a)
return a;
//走到这里说明不相同,继续递归左子树和右子树,其中一个相同就返回true。
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
5.二叉树的前序遍历


题目思路
1.求节点个数,开辟数组大小。
2.前序遍历存放到数组中
int treeSize(struct TreeNode* root)
{
if(root == NULL)
return 0;
return treeSize(root->left) + treeSize(root->right)+1;
}
void preorder(int* a, struct TreeNode* root, int* i)
{
if(root == NULL)
{
return;
}
a[(*i)++] = root->val;
preorder(a,root->left, i);
preorder(a,root->right, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
//计算树有几个节点,然后开辟相应的空间
int size = treeSize(root);
int* a = (int*)malloc(sizeof(int)* size);
int i = 0;//设置下标i
*returnSize = size;//需要返回的数组大小
//前序遍历依次存放到数组中。
preorder(a, root, &i);
return a;
}
6.反转二叉树

给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
我犯的BUG:只是对二叉树里面的值进行交换,但是无法避免空指针。一直都是空指针的错误,因为root总会为空,root->data总会遇见空指针
所以以后尽量要多想着交换地址。
void _invertTree(struct TreeNode* root)
{
if(root)
{
struct TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
_invertTree(root->left);
_invertTree(root->right);
}
}
struct TreeNode* invertTree(struct TreeNode* root)
{
_invertTree(root);
return root;
}
以上就是C语言植物大战数据结构二叉树递归的详细内容,更多关于C语言二叉树递归的资料请关注我们其它相关文章!

