C++深入细致探究二叉搜索树

目录

• 1、二叉搜索树的概念
• 2、二叉搜索树的操作
• 二叉搜索树的查找
• 二叉搜索树的插入
• 二叉搜索树的删除
• 3、二叉搜索树的实现
• 4、二叉搜索树的性能分析

1、二叉搜索树的概念

 二叉搜索树又称二叉排序树，它可以是一颗空树，亦可以是一颗具有如下性质的二叉树：

  ①若根节点的左子树不为空，则左子树上的所有节点的值域都小于根节点的值

  ②若根节点的右子树不为空，则右子树上的所有节点的值域都大于根节点的值

  ③根节点的左右子树分别也是一颗二叉搜索树

例如下面的这棵二叉树就是一棵二叉搜索树：

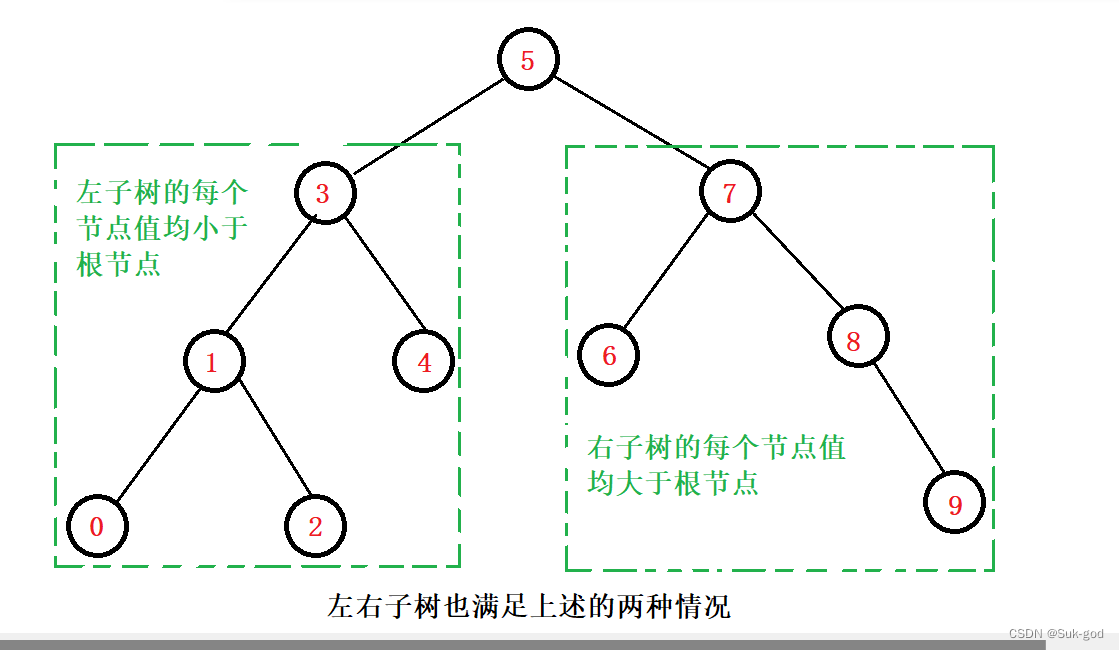
注意：判定一棵二叉树是否为二叉搜索树一定要紧扣二叉搜索树的概念~

2、二叉搜索树的操作

声明：该文章讨论的是二叉搜索树中节点值唯一的情况。

二叉搜索树的查找

对于查找部分，充分利用二叉搜索树的特性，即右子树的value 大于根节点，左子树的value小于根节点。

例如：查找下图中的红色方框中的节点

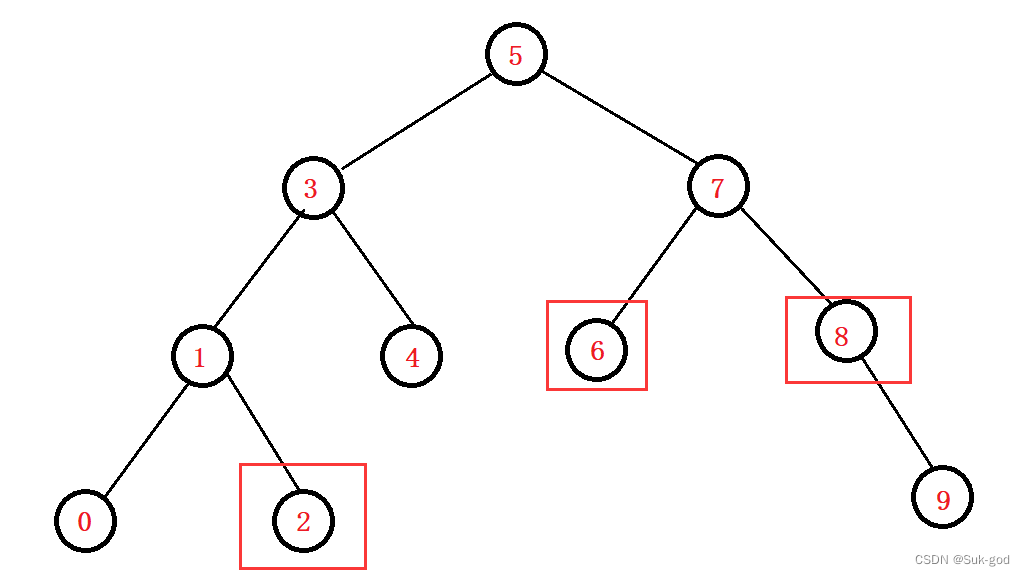
以6对应的节点为列，查找过程主要经历如下几个步骤：

  ①6与根节点5比较，6 > 5,因此到5的右子树查找

  ①6与根节点7比较，6 < 7,因此到7的左子树查找

  ①6与根节点6比较，6 == 6,此时查找成功！

总结基本步骤：

若根节点不为空：

  如果根节点的key == 查找的key----->返回true

  如果根节点的key > 查找的key----->转到根节点的右子树查找

  如果根节点的key < 查找的key----->转到根节点的左子树查找

否则（根节点为空了），直接返回false，表示树中不存在要查找的key

二叉搜索树的插入

主要分两大类的情况进行讨论：

1、树为空，直接插入

如下图所示：

2、树不空

①按照二叉搜索树的性质查找插入的位置

②插入新的节点

e.g:在下面的二叉搜索树中插入-1

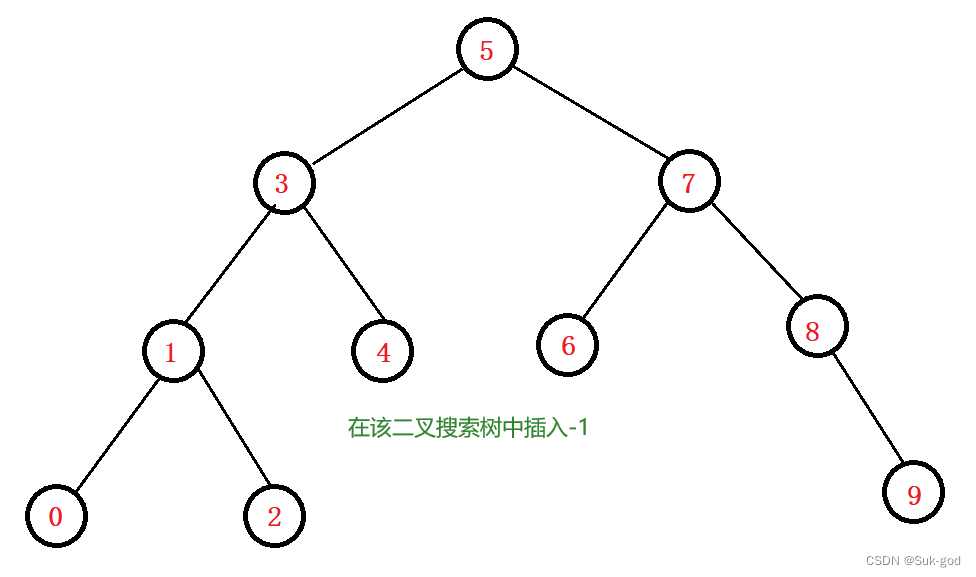
第一步，查找插入位置：

 注意：要标记当前访问的节点的双亲，否则，就算找到了插入位置，由于无法访问其双亲，也是无法进行插入的。这里使用parent来标记当前访问节点的双亲节点。

具体过程如下图：

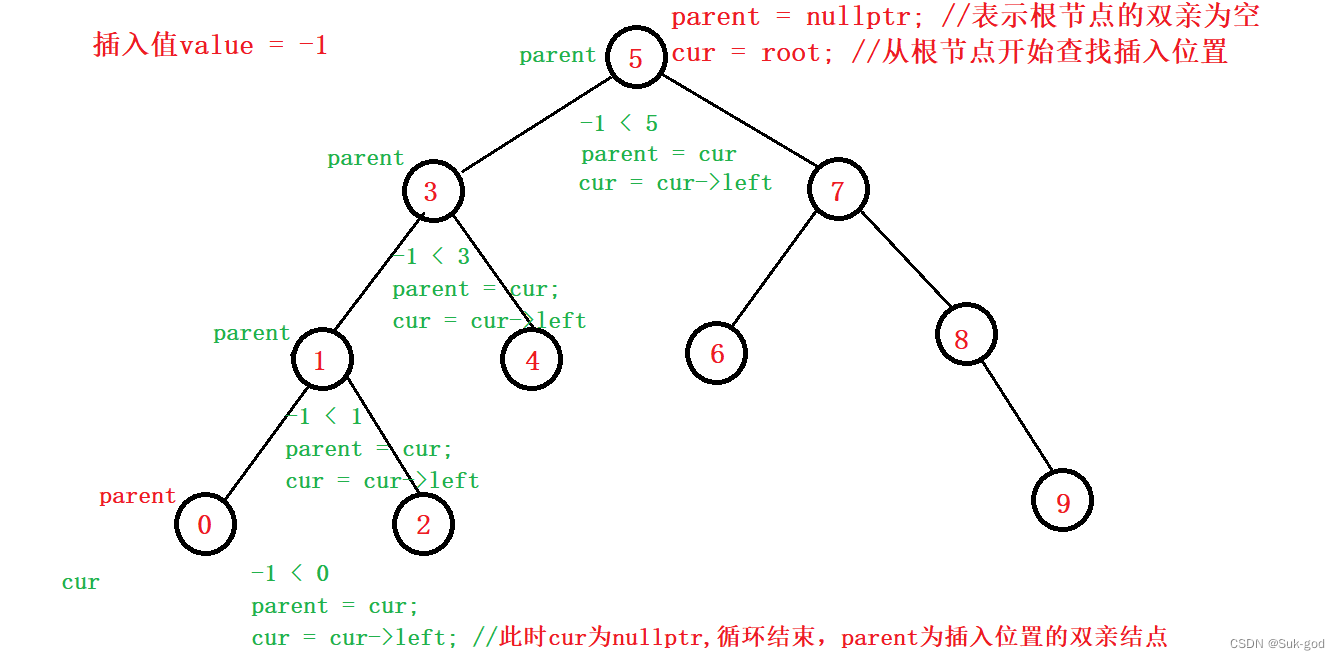
第二步，插入新节点

判断待插入节点(node)的值与parent标记的节点值的大小关系

if(node->value < parent->value)//新节点作为parent的左孩子
{
	parent->left = node;
}
else//新节点作为parent的右孩子
{
	parent->right = node;
}

以上就是二叉搜索树插入的两大类情况及其处理方式

二叉搜索树的删除

删除也是分为两大步骤：

1、找到待删除结点，并标记其双亲

具体代码片段如下：

Node* delNode = root;//标记待删除结点
Node* parent = nullptr;//标记待删除结点的双亲
while(delNode)
{
	if(delNode->value == value)
	{
		break;
	}
	else if(delNode->value > value)
	{
		parent = delNode;
		delNode = delNode->left;
	}
	else
	{
		parent = delNode;
		delNode = delNode->right;
	}
}

上述代码执行完毕后，delNode有两种情况，delNode == nullptr || delNode!=nullptr

下面我们就这两种情况展开讨论：

2、删除该节点

Ⅰ、nullptr == delNode

  说明在二叉搜索树中不存在要删除的结点。直接return false；

Ⅱ、delNode != nullptr;

  在二叉搜索树中找到了删除结点，开始删除。

删除时，对于待删除结点要根据其孩子节点分情况讨论：

  ①待删除结点是叶子结点

  ②待删除结点只有左孩子

  ③待删除结点只有有孩子

  ④待删除结点左右孩子均存在

下面，我们就这4中情况展开讨论：

情况一：待删除结点时叶子节点

可以直接删除，具体如下图：

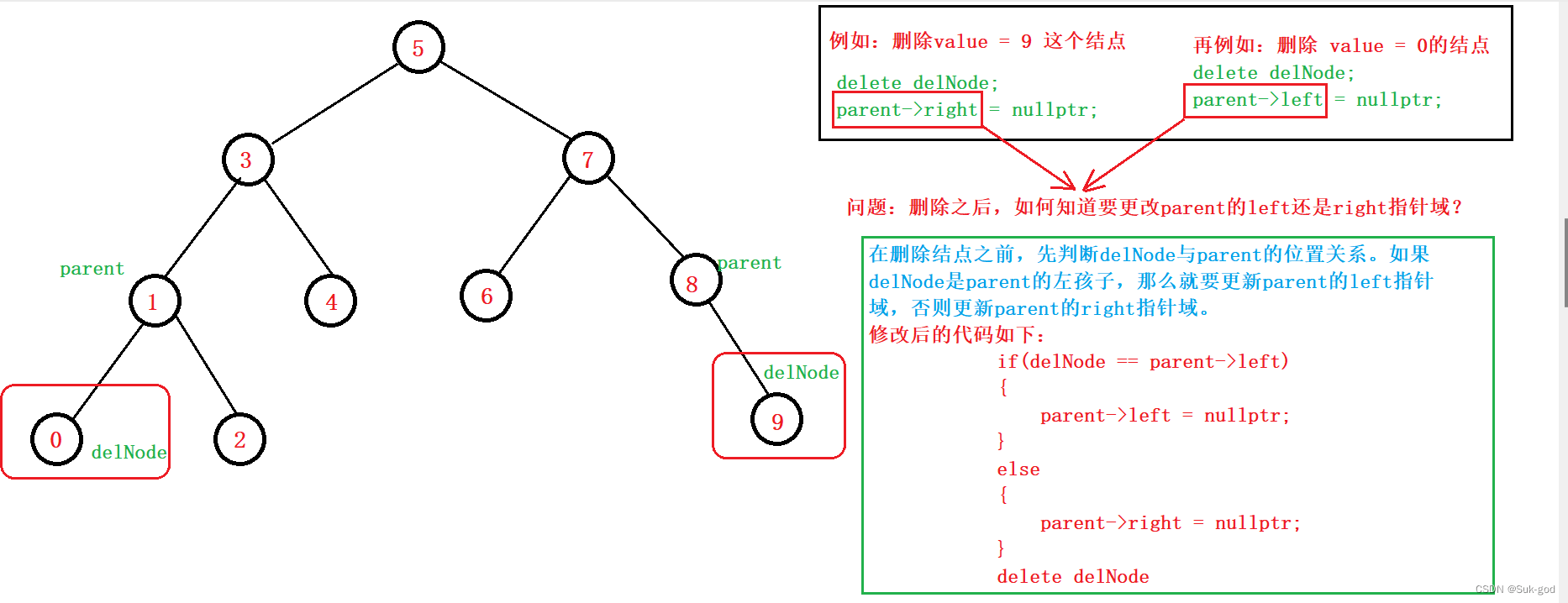
情况二：待删除结点只有左孩子

在此前提下，有两类情形

1、delNode的双亲存在  

2、delNode的双亲不存在

下面就这两种情况展开讨论：

1、delNode的双亲存在

删除过程见下图：

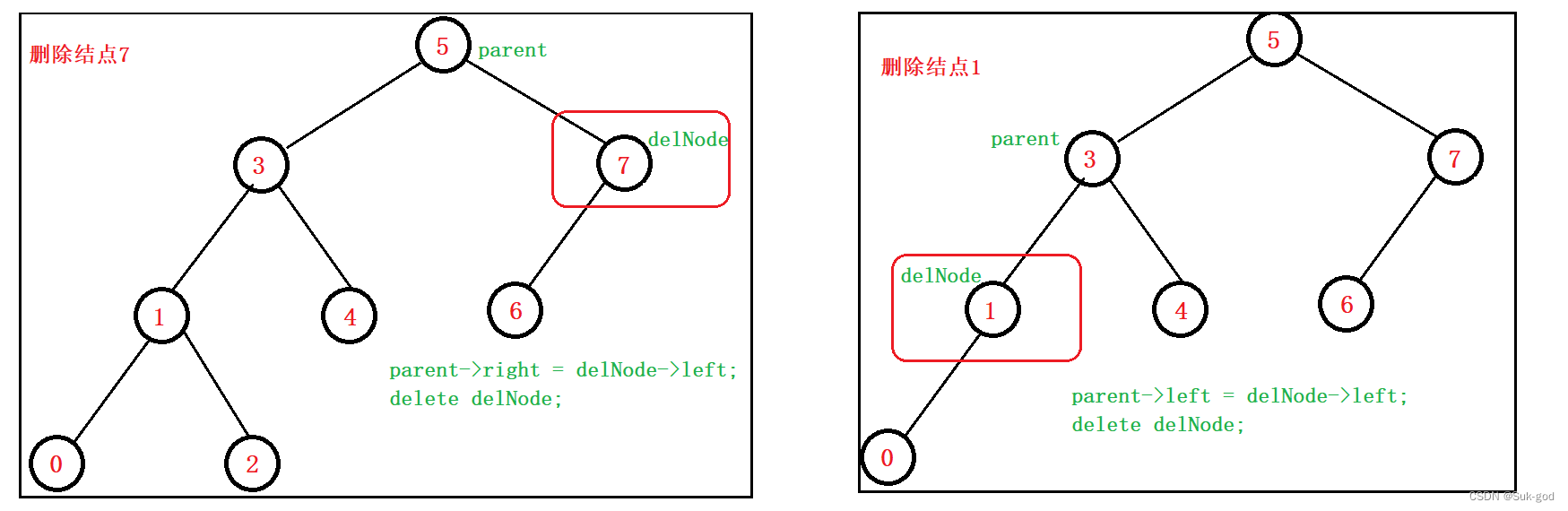
2、delNode的双亲不存在

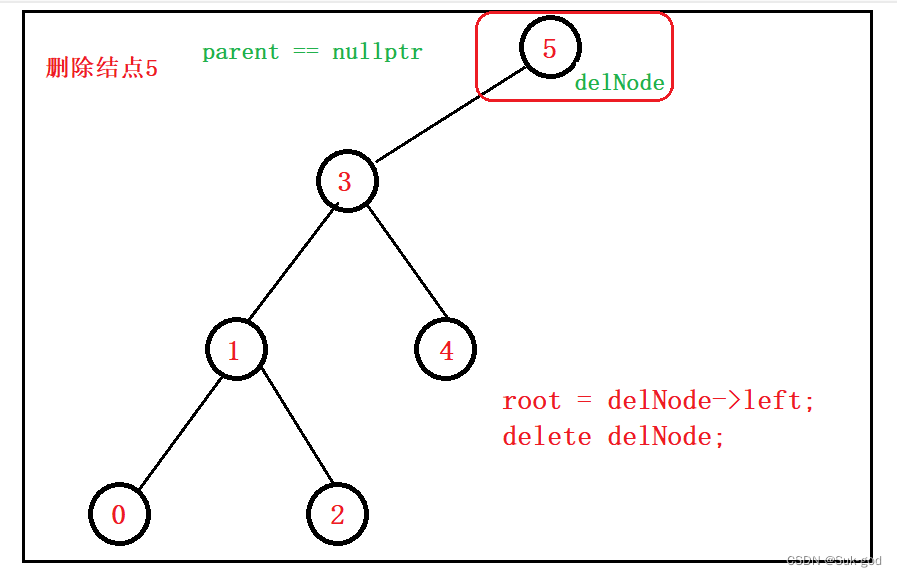
与上述仅存在叶子节点时存在的问题一样，需要在delete待删除结点之前，判断delNode与parent的位置关系，进而确定是更新parent的left指针域还是right指针域

结合上述两种情况，初步确定仅有左孩子的删除代码片段如下：

if(nullptr == parent)
{
	root = delNode->left;
}
else
{
	if(delNode == parent->left)
	{
		parent->left = delNode->left;
	}
	else
	{
		parent->right = delNode->left;
	}
}
delete delNode;

我们结合删除节点是叶子节点 && 删除节点仅有左子树两种情况来看，发现这两种情况可以进行合并。合并后的代码如下图：

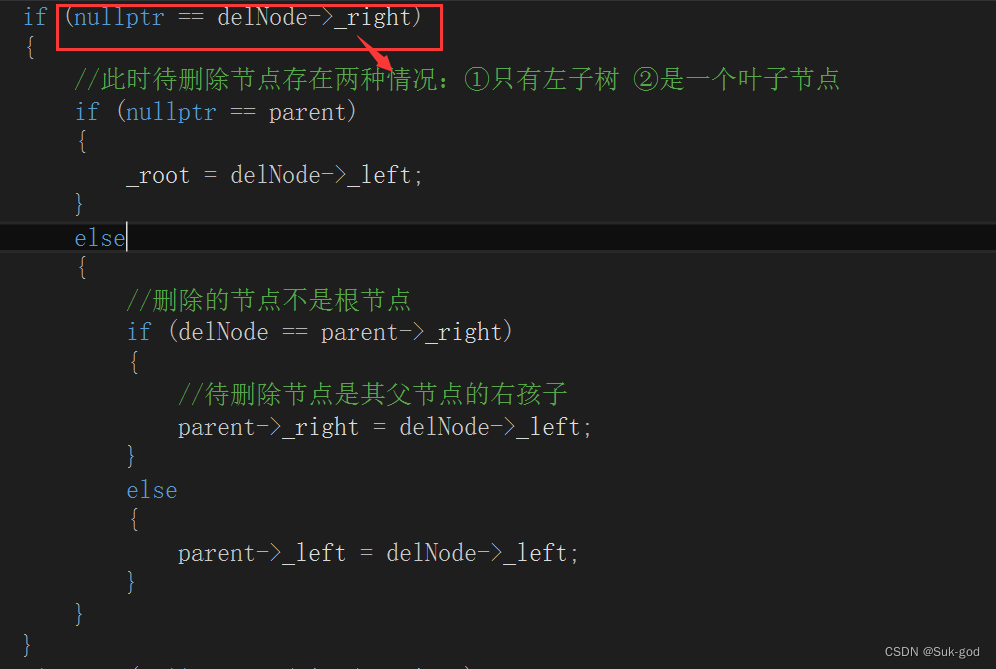
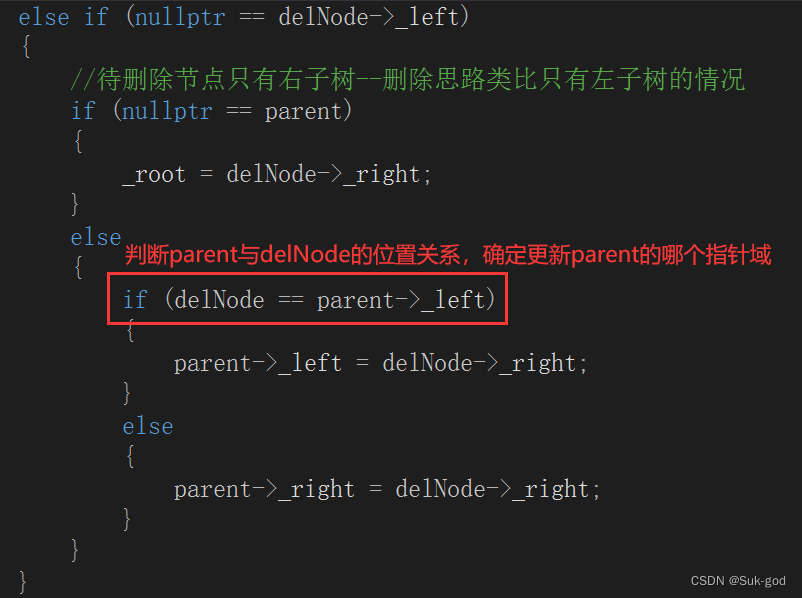
情况三：待删除结点只有右孩子

该情况与只有左孩子的分析过程一样，存在两类情形，分别是

1、delNode的双亲存在  

2、delNode的双亲不存在

这里不再进行分析，直接给出代码：

情况四：待删除结点左右孩子均存在

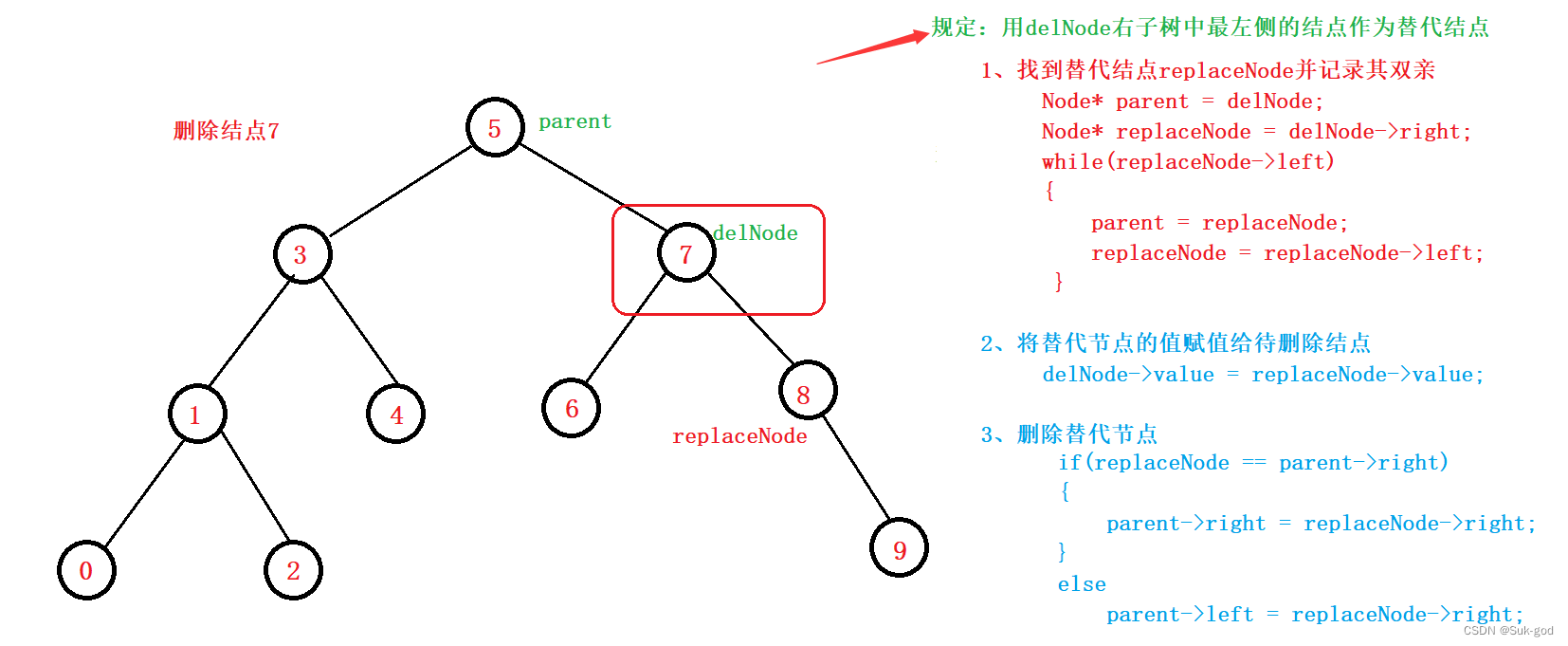
明确：该情况无法直接删除，需要在其子树中寻找替代结点 具体删除步骤如下：

1、找替代节点：在delNode的右子树（左子树）找最左侧（最右侧）的结点并保存其双亲

2、将替代节点中的值域赋值给待删除结点

3、将替代节点删除掉

①如果替代节点找的是delNode右子树的最左侧结点，那么待删除的替代节点一定不会有左子树，可能会有右子树

②如果替代节点找的是delNode左子树的最右侧结点，那么待删除的替代节点一定不会有右子树，可能会有左子树 注意：一般情况下采用delNode右子树的最左侧结点作为替代节点

具体过程见下图：

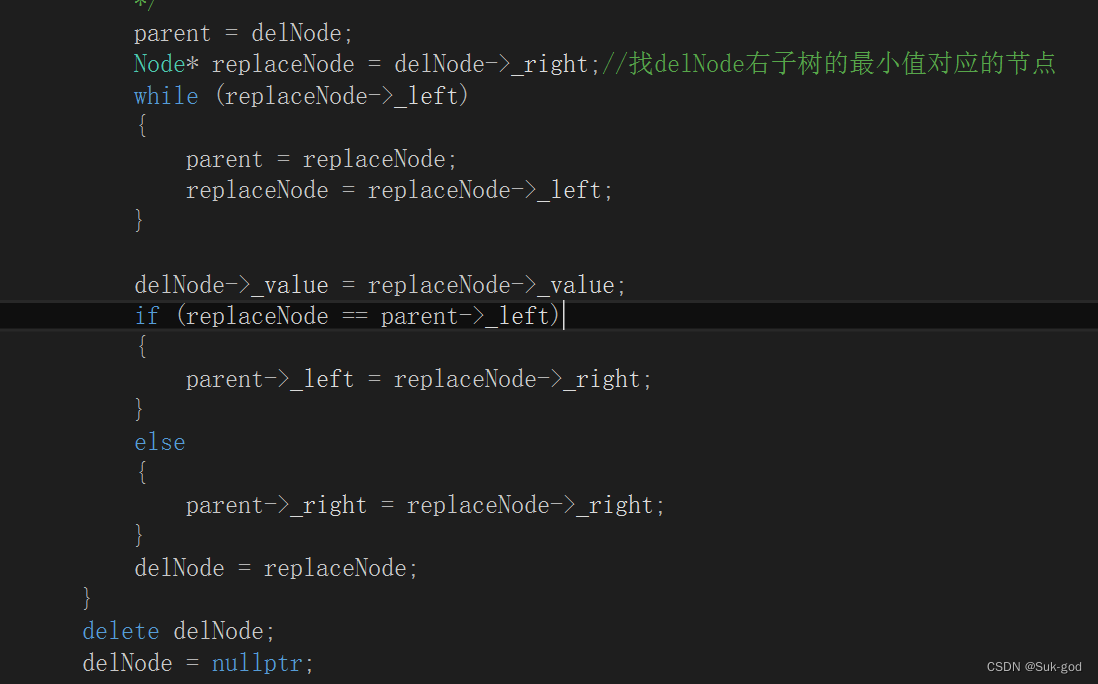
ok,下面给出实现的代码：

3、二叉搜索树的实现

数据结构：

template<class T>
struct BSTNode//每一个结点的结构
{
	BSTNode<T>* _left;//左指针域
	BSTNode<T>* _right;//右指针域
	T _value;//值域

	BSTNode(const T& value = T())
		:_left(nullptr)
		, _right(nullptr)
		, _value(value)
	{}
};

采用模板的方式实现，具体代码见 BinarySearchTree

4、二叉搜索树的性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能

对于有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数。即结点越深，比较次数越多。

但对于同一个关键码的集合，如果各关键码插入的次序不同，可能会得到不同的二叉搜索树：

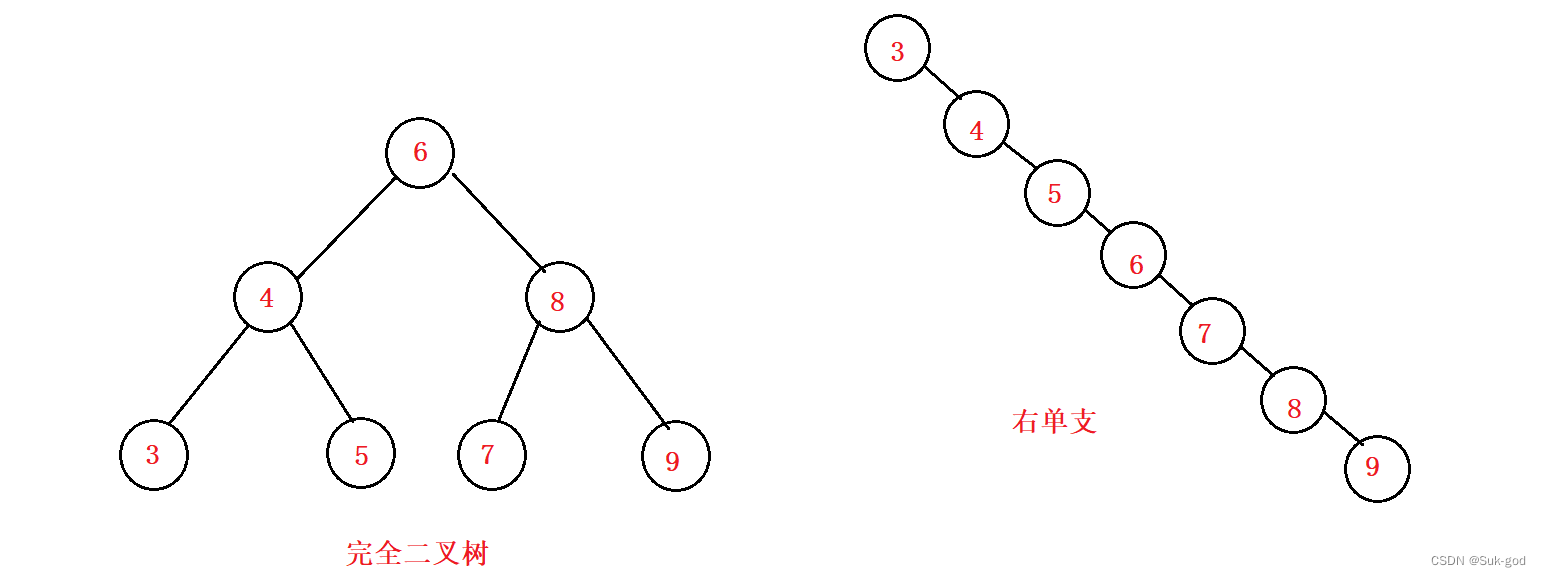
最优情况下：二叉搜索树为完全二叉树，其平均比较次数为log2N

最差情况下：二叉搜索树退化为单支树，其平均比较次数为N/2

因此，二叉搜索树的时间复杂度为O(log2N)

到此这篇关于C++深入细致探究二叉搜索树的文章就介绍到这了,更多相关C++二叉搜索树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！