python实现门限回归方式
门限回归模型(Threshold Regressive Model,简称TR模型或TRM)的基本思想是通过门限变量的控制作用,当给出预报因子资料后,首先根据门限变量的门限阈值的判别控制作用,以决定不同情况下使用不同的预报方程,从而试图解释各种类似于跳跃和突变的现象。其实质上是把预报问题按状态空间的取值进行分类,用分段的线性回归模式来描述总体非线性预报问题。
多元门限回归的建模步骤就是确实门限变量、率定门限数L、门限值及回归系数的过程,为了计算方便,这里采用二分割(即L=2)说明模型的建模步骤。
基本步骤如下(附代码):
1.读取数据,计算预报对象与预报因子之间的互相关系数矩阵。
数据读取
#利用pandas读取csv,读取的数据为DataFrame对象
data = pd.read_csv('jl.csv')
# 将DataFrame对象转化为数组,数组的第一列为数据序号,最后一列为预报对象,中间各列为预报因子
data= data.values.copy()
# print(data)
# 计算互相关系数,参数为预报因子序列和滞时k
def get_regre_coef(X,Y,k):
S_xy=0
S_xx=0
S_yy=0
# 计算预报因子和预报对象的均值
X_mean = np.mean(X)
Y_mean = np.mean(Y)
for i in range(len(X)-k):
S_xy += (X[i] - X_mean) * (Y[i+k] - Y_mean)
for i in range(len(X)):
S_xx += pow(X[i] - X_mean, 2)
S_yy += pow(Y[i] - Y_mean, 2)
return S_xy/pow(S_xx*S_yy,0.5)
#计算相关系数矩阵
def regre_coef_matrix(data):
row=data.shape[1]#列数
r_matrix=np.ones((1,row-2))
# print(row)
for i in range(1,row-1):
r_matrix[0,i-1]=get_regre_coef(data[:,i],data[:,row-1],1)#滞时为1
return r_matrix
r_matrix=regre_coef_matrix(data)
# print(r_matrix)
###输出###
#[[0.048979 0.07829989 0.19005705 0.27501209 0.28604638]]
2.对相关系数进行排序,相关系数最大的因子作为门限元。
#对相关系数进行排序找到相关系数最大者作为门限元 def get_menxiannum(r_matrix): row=r_matrix.shape[1]#列数 for i in range(row): if r_matrix.max()==r_matrix[0,i]: return i+1 return -1 m=get_menxiannum(r_matrix) # print(m) ##输出##第五个因子的互相关系数最大 #5
3.根据选取的门限元因子对数据进行重新排序。
#根据门限元对因子序列进行排序,m为门限变量的序号 def resort_bymenxian(data,m): data=data.tolist()#转化为列表 data.sort(key=lambda x: x[m])#列表按照m+1列进行排序(升序) data=np.array(data) return data data=resort_bymenxian(data,m)#得到排序后的序列数组
4.将排序后的序列按照门限元分割序列为两段,第一分割第一段1个数据,第二段n-1(n为样本容量)个数据;第二次分割第一段2个数据,第二段n-2个数据,一次类推,分别计算出分割后的F统计量并选出最大统计量对应的门限元的分割点作为门限值。
def get_var(x): return x.std() ** 2 * x.size # 计算总方差 #统计量F的计算,输入数据为按照门限元排序后的预报对象数据 def get_F(Y): col=Y.shape[0]#行数,样本容量 FF=np.ones((1,col-1))#存储不同分割点的统计量 V=get_var(Y)#计算总方差 for i in range(1,col):#1到col-1 S=get_var(Y[0:i])+get_var(Y[i:col])#计算两段的组内方差和 F=(V-S)*(col-2)/S FF[0,i-1]=F#此步需要判断是否通过F检验,通过了才保留F统计量 return FF y=data[:,data.shape[1]-1] FF=get_F(y) def get_index(FF,element):#获取element在一维数组FF中第一次出现的索引 i=-1 for item in FF.flat: i+=1 if item==element: return i f_index=get_index(FF,np.max(FF))#获取统计量F的最大索引 # print(data[f_index,m-1])#门限元为第五个因子,代入索引得门限值 121
5.以门限值为分割点将数据序列分割为两段,分别进行多元线性回归,此处利用sklearn.linear_model模块中的线性回归模块。再代入预报因子分别计算两段的预测值。
#以门限值为分割点将新data序列分为两部分,分别进行多元回归计算
def data_excision(data,f_index):
f_index=f_index+1
data1=data[0:f_index,:]
data2=data[f_index:data.shape[0],:]
return data1,data2
data1,data2=data_excision(data,f_index)
# 第一段
def get_XY(data):
# 数组切片对变量进行赋值
Y = data[:, data.shape[1] - 1] # 预报对象位于最后一列
X = data[:, 1:data.shape[1] - 1]#预报因子从第二列到倒数第二列
return X, Y
X,Y=get_XY(data1)
regs=LinearRegression()
regs.fit(X,Y)
# print('第一段')
# print(regs.coef_)#输出回归系数
# print(regs.score(X,Y))#输出相关系数
#计算预测值
Y1=regs.predict(X)
# print('第二段')
X,Y=get_XY(data2)
regs.fit(X,Y)
# print(regs.coef_)#输出回归系数
# print(regs.score(X,Y))#输出相关系数
#计算预测值
Y2=regs.predict(X)
Y=np.column_stack((data[:,0],np.hstack((Y1,Y2)))).copy()
Y=np.column_stack((Y,data[:,data.shape[1]-1]))
Y=resort_bymenxian(Y,0)
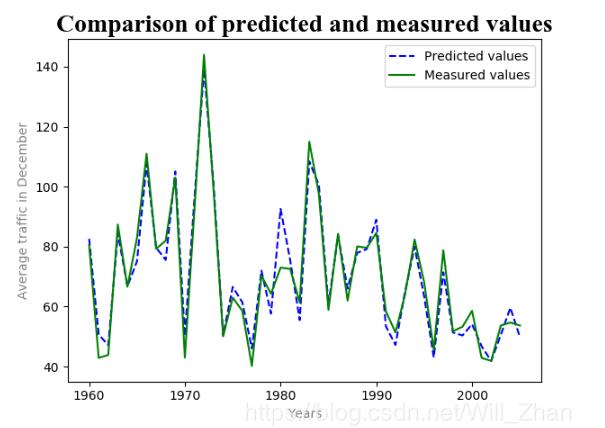
6.将预测值和实际值按照年份序号从新排序,恢复其顺序,利用matplotlib模块做出预测值与实际值得对比图。
#恢复顺序
Y=resort_bymenxian(Y,0)
# print(Y.shape)
# 预测结果可视化
plt.plot(Y[:,0],Y[:,1],'b--',Y[:,0],Y[:,2],'g')
plt.title('Comparison of predicted and measured values',fontsize=20,fontname='Times New Roman')#添加标题
plt.xlabel('Years',color='gray')#添加x轴标签
plt.ylabel('Average traffic in December',color='gray')#添加y轴标签
plt.legend(['Predicted values','Measured values'])#添加图例
plt.show()
结果图:
所用数据:引自《现代中长期水文预报方法及其应用》汤成友 官学文 张世明 著
| num | x1 | x2 | x3 | x4 | x5 | y |
| 1960 | 308 | 301 | 352 | 310 | 149 | 80.5 |
| 1961 | 182 | 186 | 165 | 127 | 70 | 42.9 |
| 1962 | 195 | 134 | 134 | 97 | 61 | 43.9 |
| 1963 | 136 | 378 | 334 | 307 | 148 | 87.4 |
| 1964 | 230 | 630 | 332 | 161 | 100 | 66.6 |
| 1965 | 225 | 333 | 209 | 365 | 152 | 82.9 |
| 1966 | 296 | 225 | 317 | 527 | 228 | 111 |
| 1967 | 324 | 229 | 176 | 317 | 153 | 79.3 |
| 1968 | 278 | 230 | 352 | 317 | 143 | 82 |
| 1969 | 662 | 442 | 453 | 381 | 188 | 103 |
| 1970 | 187 | 136 | 103 | 129 | 74.7 | 43 |
| 1971 | 284 | 404 | 600 | 327 | 161 | 92.2 |
| 1972 | 427 | 430 | 843 | 448 | 236 | 144 |
| 1973 | 258 | 404 | 639 | 275 | 156 | 98.9 |
| 1974 | 113 | 160 | 128 | 177 | 77.2 | 50.1 |
| 1975 | 143 | 300 | 333 | 214 | 106 | 63 |
| 1976 | 113 | 74 | 193 | 241 | 107 | 58.6 |
| 1977 | 204 | 140 | 154 | 90 | 55.1 | 40.2 |
| 1978 | 174 | 445 | 351 | 267 | 120 | 70.3 |
| 1979 | 93 | 95 | 197 | 214 | 94.9 | 64.3 |
| 1980 | 214 | 250 | 354 | 385 | 178 | 73 |
| 1981 | 232 | 676 | 483 | 218 | 113 | 72.6 |
| 1982 | 266 | 216 | 146 | 112 | 82.8 | 61.4 |
| 1983 | 210 | 433 | 803 | 301 | 166 | 115 |
| 1984 | 261 | 702 | 512 | 291 | 153 | 97.5 |
| 1985 | 197 | 178 | 238 | 180 | 94.2 | 58.9 |
| 1986 | 442 | 256 | 623 | 310 | 146 | 84.3 |
| 1987 | 136 | 99 | 253 | 232 | 114 | 62 |
| 1988 | 256 | 226 | 185 | 321 | 151 | 80.1 |
| 1989 | 473 | 409 | 300 | 298 | 141 | 79.6 |
| 1990 | 277 | 291 | 639 | 302 | 149 | 84.6 |
| 1991 | 372 | 181 | 174 | 104 | 68.8 | 58.4 |
| 1992 | 251 | 142 | 126 | 95 | 59.4 | 51.4 |
| 1993 | 181 | 125 | 130 | 240 | 121 | 64 |
| 1994 | 253 | 278 | 216 | 182 | 124 | 82.4 |
| 1995 | 168 | 214 | 265 | 175 | 101 | 68.1 |
| 1996 | 98.8 | 97 | 92.7 | 88 | 56.7 | 45.6 |
| 1997 | 252 | 385 | 313 | 270 | 119 | 78.8 |
| 1998 | 242 | 198 | 137 | 114 | 71.9 | 51.8 |
| 1999 | 268 | 178 | 127 | 109 | 68.6 | 53.3 |
| 2000 | 86.2 | 286 | 233 | 133 | 77.8 | 58.6 |
| 2001 | 150 | 168 | 122 | 93 | 62.8 | 42.9 |
| 2002 | 180 | 150 | 97.8 | 78 | 48.2 | 41.9 |
| 2003 | 166 | 203 | 166 | 124 | 70 | 53.7 |
| 2004 | 400 | 202 | 126 | 158 | 92.7 | 54.7 |
| 2005 | 79.8 | 82.6 | 129 | 160 | 76.6 | 53.7 |
以上这篇python实现门限回归方式就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持我们。
赞 (0)

