原生python实现knn分类算法

一、题目要求

用原生Python实现knn分类算法。

二、题目分析

数据来源：鸢尾花数据集（见附录Iris.txt）

数据集包含150个数据集，分为3类，分别是：Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾）和Iris Virginica（维吉尼亚鸢尾）。每类有50个数据，每个数据包含四个属性，分别是：Sepal.Length（花萼长度）、Sepal.Width（花萼宽度）、Petal.Length（花瓣长度）和Petal.Width（花瓣宽度）。

将得到的数据集按照7:3的比例划分，其中7为训练集，3为测试集。编写算法实现：学习训练集的数据特征来预测测试集鸢尾花的种类，并且计算出预测的准确性。

KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

三、算法设计

1）将文本文件按行分割，写入列表datas中

def data_read(filepath): # 读取txt文件，将读出的内容存入datas列表中
  fp = open(filepath, "r")
  datas = [] # 存储处理后的数据
  lines = fp.readlines() # 读取整个文件数据
  for line in lines:
    row = line.strip('\n').split(',') # 去除两头的换行符，按空格分割
    datas.append(row)
  fp.close()
  return datas

2）划分数据集与测试集，将数据集的数据存入labeldata_list列表，标签存入label_list列表，测试集数据存入text_list列表，标签存入textlabel_list列表。

3）对得到的两个数据集的数据和标签列表进行处理。将labeldata_list列表数据转换为元组labeldata_tuple，构造形入{labeldata_tuple: label_list}的字典mydict。这样不仅可以去掉重复数据，而且可唯一的标识各个数据所对应的鸢尾花种类。

for i in range(0, 105): # 数据集按照3:7的比例划分，其中105行为训练集，45行为测试集
  labeldata_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
  label_list.append(datas[i][4])

for i in range(105, 150): # 测试集的数据
  text_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
  textlabel_list.append(datas[i][4])

j = 0
for i in labeldata_list:
  labeldata_tuple = tuple(i)
  mydict.update({labeldata_tuple: label_list[j]})
  j = j + 1

4）计算测试集数据与各个训练集数据之间的距离，得到distance_list列表，外层循环进行一次，都会有一个该测试数据所对应的与训练数据最短距离。标记出该距离对应的训练集，在一个近邻的条件下，这个训练集的种类，就是该测试集的种类。
在计算距离时，使用绝对距离来计算。将每个训练集对应数据的属性值相减后求和add，得到一个测试数据与每个样本的距离，add的最小值就是距离最小值。

for i in range(len(text_list)):
  count += 1
  for j in range(len(train_list)):
    add1 = abs(float(train_list[j][0]) - float(text_list[i][0])) + abs(float(train_list[j][1])
                                      - float(text_list[i][1])) + abs(
      float(train_list[j][2]) - float(text_list[i][2])) + abs(float(train_list[j][3])
                                  - float(text_list[i][3]))
    distance_list.append(add1)
    if add > add1:
      add = add1
      index = train_list[j]
  print("预测", text_list[i], "的标签是：", mydict.get(index))

5）判断预测结果的准确性：将预测的测试数据种类与原始数据对比，若相同，则分子加一。

right = 0 # 分子
count = 0 # 分母
for i in range(len(text_list)):
  count += 1
  for j in range(len(train_list)):
    add1 = abs(float(train_list[j][0]) - float(text_list[i][0])) + abs(float(train_list[j][1])
                                      - float(text_list[i][1])) + abs(
      float(train_list[j][2]) - float(text_list[i][2])) + abs(float(train_list[j][3])
                                  - float(text_list[i][3]))
    distance_list.append(add1)
    if add > add1:
      add = add1
      index = train_list[j]
  print("预测", text_list[i], "的标签是：", mydict.get(index))
  if mydict.get(index) == textlabel_list[i]: # 当计算出来的1个近邻与测试集正确的标签相同时，分子加一
    right = right + 1
print('预测准确性：{:.2f}'.format(right / count))

6）举例，绘图

以测试集7.6,3.0,6.6,2.1,Iris-virginica为例：
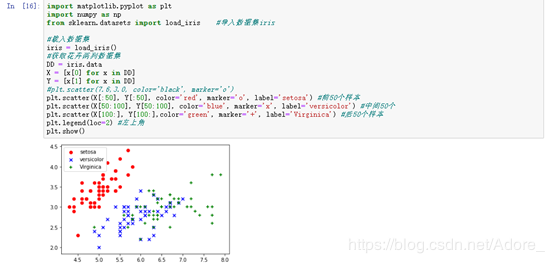
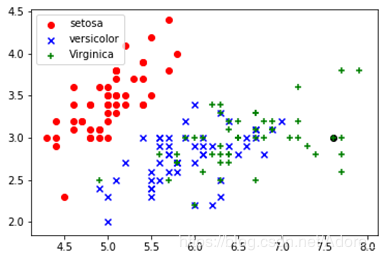
首先运用anaconda绘制出数据集的散点图，其次，将需要测试的数据于数据集绘制在同一张图上，在一个近邻的前提下，距离测试数据最近的点的标签即为测试数据的的标签。如下图，黑色的测试点距离红点最近，所以，测试数据的标签就为virginica。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris  #导入数据集iris

#载入数据集
iris = load_iris()
#获取花卉两列数据集
DD = iris.data
X = [x[0] for x in DD]
Y = [x[1] for x in DD]
#plt.scatter(7.6,3.0, color='black', marker='o')
plt.scatter(X[:50], Y[:50], color='red', marker='o', label='setosa') #前50个样本
plt.scatter(X[50:100], Y[50:100], color='blue', marker='x', label='versicolor') #中间50个
plt.scatter(X[100:], Y[100:],color='green', marker='+', label='Virginica') #后50个样本
plt.legend(loc=2) #左上角
plt.show()

算法数据流图：

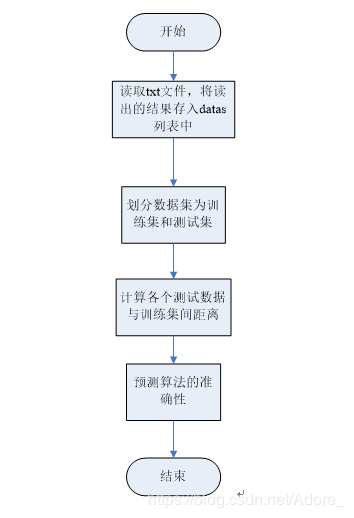
计算各个测试数据与训练集间距离详细流程图：

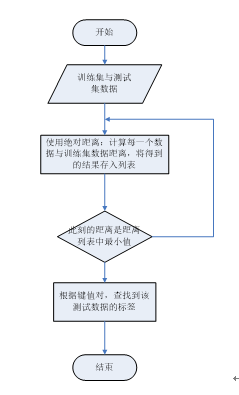
五、测试

导入数据集

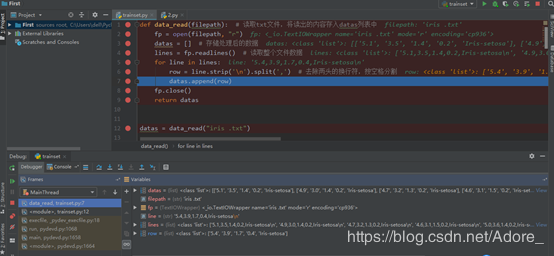
划分数据集

训练集：

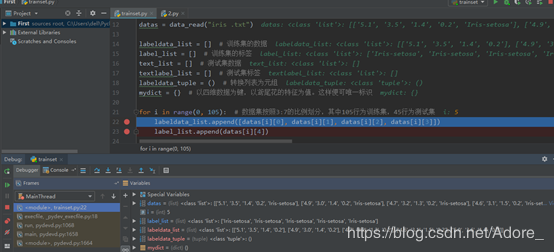
测试集：

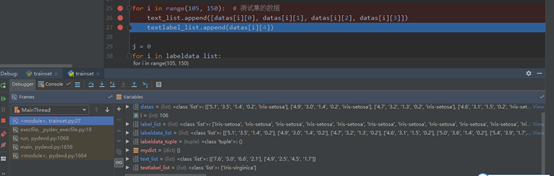
对得到的两个数据集的数据和标签列表进行处理

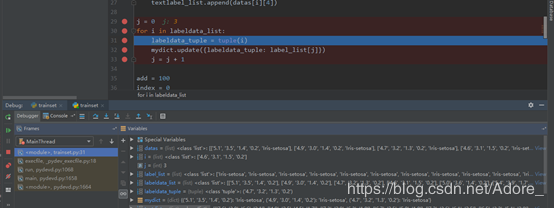
计算测试集数据与各个训练集数据之间的距离

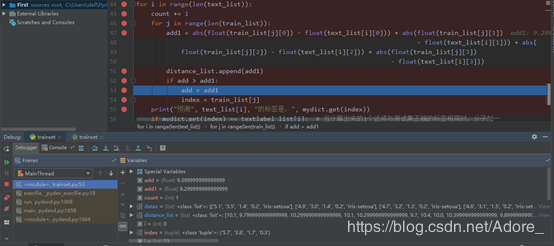
判断预测结果的准确性

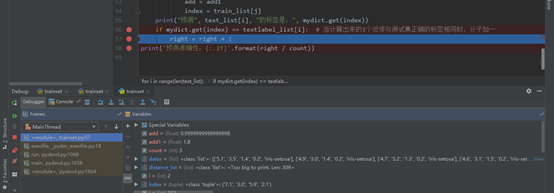
绘图举例

五、运行结果

1.对测试集所有数据进行预测，得到预测测试集的标签与预测准确性

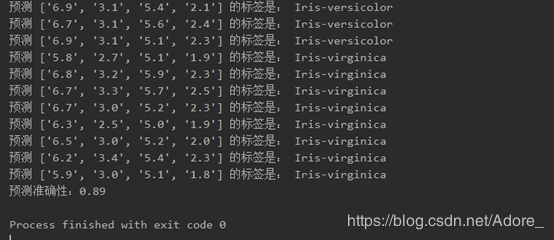
绘出散点图：7.6,3.0,6.6,2.1,Iris-virginica作为测试集的举例

六、总结

学习了关于绘图的函数与库
发现在绘图方面anaconde比pycharm要方便的多

对向量之间的距离公式进行了复习
除了这次作业中使用到的绝对距离之外，还有：
a)欧氏距离
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离：

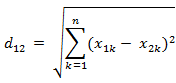
b)曼哈顿距离
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离

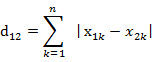
c)闵可夫斯基距离
两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

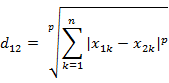
对文件的读操作进行使用

算法缺点：用了许多for循环，会降低效率，增加算法的时间复杂度；只是一个近邻的判断依据

七、源代码

def data_read(filepath): # 读取txt文件，将读出的内容存入datas列表中
  fp = open(filepath, "r")
  datas = [] # 存储处理后的数据
  lines = fp.readlines() # 读取整个文件数据
  for line in lines:
    row = line.strip('\n').split(',') # 去除两头的换行符，按空格分割
    datas.append(row)
  fp.close()
  return datas

datas = data_read("iris .txt")

labeldata_list = [] # 训练集的数据
label_list = [] # 训练集的标签
text_list = [] # 测试集数据
textlabel_list = [] # 测试集标签
labeldata_tuple = () # 转换列表为元组
mydict = {} # 以四维数据为键，以鸢尾花的特征为值。这样便可唯一标识

'''
划分数据集与测试集，将数据集的数据存入labeldata_list列表，标签存入label_list列表，
测试集数据存入text_list列表，标签存入textlabel_list列表。
'''
for i in range(0, 105): # 数据集按照3:7的比例划分，其中105行为训练集，45行为测试集
  labeldata_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
  label_list.append(datas[i][4])

for i in range(105, 150): # 测试集的数据
  text_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
  textlabel_list.append(datas[i][4])

j = 0
for i in labeldata_list:
  labeldata_tuple = tuple(i)
  mydict.update({labeldata_tuple: label_list[j]})
  j = j + 1

add = 100
index = 0
distance_list = []
train_list = []
for key, value in mydict.items():
  train_list.append(key)

right = 0 # 分子
count = 0 # 分母
'''
在计算距离时，使用绝对距离来计算。
将每个训练集对应数据的属性值相减后求和add，
得到一个测试数据与每个样本的距离，add的最小值就是距离最小值。
'''
for i in range(len(text_list)):
  count += 1
  for j in range(len(train_list)):
    add1 = abs(float(train_list[j][0]) - float(text_list[i][0])) + abs(float(train_list[j][1])
                                      - float(text_list[i][1])) + abs(
      float(train_list[j][2]) - float(text_list[i][2])) + abs(float(train_list[j][3])
                                  - float(text_list[i][3]))
    distance_list.append(add1)
    if add > add1:
      add = add1
      index = train_list[j]
  print("预测", text_list[i], "的标签是：", mydict.get(index))
  if mydict.get(index) == textlabel_list[i]: # 当计算出来的1个近邻与测试集正确的标签相同时，分子加一
    right = right + 1
print('预测准确性：{:.2f}'.format(right / count))

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。