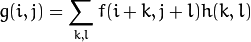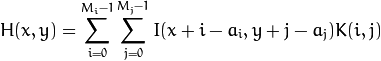Javascript图像处理—平滑处理实现原理

前言

上一篇文章，我们讲解了图像的虚拟边缘，这篇文章开始进行平滑（也就是模糊）处理。

基本原理

这里直接引用OpenCV 2.4+ C++ 平滑处理和OpenCV 2.4+ C++ 边缘梯度计算的相关内容：

平滑也称模糊, 是一项简单且使用频率很高的图像处理方法。

平滑处理时需要用到一个滤波器

。 最常用的滤波器是线性
滤波器，线性滤波处理的输出像素值（例如：）是输入像素值（例如：）的加权平均：

　　　　

称为核

, 它仅仅是一个加权系数。

这里涉及一种叫做“卷积”的运算，那么卷积是什么呢？

卷积是在每一个图像块与某个算子（核）之间进行的运算。

核？！

nbsp;
dsds

核就是一个固定大小的数值数组。该数组带有一个锚点

，一般位于数组中央。

可是这怎么运算啊？

假如你想得到图像的某个特定位置的卷积值，可用下列方法计算：

将核的锚点放在该特定位置的像素上，同时，核内的其他值与该像素邻域的各像素重合；将核内各值与相应像素值相乘，并将乘积相加；将所得结果放到与锚点对应的像素上；对图像所有像素重复上述过程。

用公式表示上述过程如下：

　　　　

在图像边缘的卷积怎么办呢？

计算卷积前，需要通过复制源图像的边界创建虚拟像素，这样边缘的地方也有足够像素计算卷积了。这就是为什么上一篇文章需要做虚拟边缘函数。

均值平滑

均值平滑实际上就是内核元素全是1的卷积运算，然后再除以内核的大小，用数学表达式来表示就是：

下面我们来实现均值平滑函数blur：


代码如下:

function blur(__src, __size1, __size2, __borderType, __dst){
if(__src.type && __src.type == "CV_RGBA"){
var height = __src.row,
width = __src.col,
dst = __dst || new Mat(height, width, CV_RGBA),
dstData = dst.data;
var size1 = __size1 || 3,
size2 = __size2 || size1,
size = size1 * size2;
if(size1 % 2 !== 1 || size2 % 2 !== 1){
console.error("size大小必须是奇数");
return __src;
}
var startX = Math.floor(size1 / 2),
startY = Math.floor(size2 / 2);
var withBorderMat = copyMakeBorder(__src, startY, startX, 0, 0, __borderType),
mData = withBorderMat.data,
mWidth = withBorderMat.col;

var newValue, nowX, offsetY, offsetI;
var i, j, c, y, x;

for(i = height; i--;){
offsetI = i * width;
for(j = width; j--;){
for(c = 3; c--;){
newValue = 0;
for(y = size2; y--;){
offsetY = (y + i) * mWidth * 4;
for(x = size1; x--;){
nowX = (x + j) * 4 + c;
newValue += mData[offsetY + nowX];
}
}
dstData[(j + offsetI) * 4 + c] = newValue / size;
}
dstData[(j + offsetI) * 4 + 3] = mData[offsetY + startY * mWidth * 4 + (j + startX) * 4 + 3];
}
}

}else{
console.error("不支持类型。");
}
return dst;
}

其中size1和size2分别是核的横向和纵向大小，并且必须是正奇数。

高斯平滑

最有用的滤波器 (尽管不是最快的)。 高斯滤波是将输入数组的每一个像素点与高斯内核

卷积将卷积和当作输出像素值。

参考一维高斯函数，我们可以看见，他是个中间大两边小的函数。

所以高斯滤波器其加权数是中间大，四周小的。

其二维高斯函数为：

其中

 为均值 (峰值对应位置)，

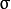 代表标准差 (变量
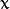 和 变量
 各有一个均值，也各有一个标准差)。

这里参考OpenCV的实现，不过应该还有优化空间，因为还没用到分离滤波器。

首先我们做一个getGaussianKernel来返回高斯滤波器的一维数组。


代码如下:

function getGaussianKernel(__n, __sigma){
var SMALL_GAUSSIAN_SIZE = 7,
smallGaussianTab = [[1],
[0.25, 0.5, 0.25],
[0.0625, 0.25, 0.375, 0.25, 0.0625],
[0.03125, 0.109375, 0.21875, 0.28125, 0.21875, 0.109375, 0.03125]
];

var fixedKernel = __n & 2 == 1 && __n <= SMALL_GAUSSIAN_SIZE && __sigma <= 0 ? smallGaussianTab[__n >> 1] : 0;

var sigmaX = __sigma > 0 ? __sigma : ((__n - 1) * 0.5 - 1) * 0.3 + 0.8,
scale2X = -0.5 / (sigmaX * sigmaX),
sum = 0;

var i, x, t, kernel = [];

for(i = 0; i < __n; i++){
x = i - (__n - 1) * 0.5;
t = fixedKernel ? fixedKernel[i] : Math.exp(scale2X * x * x);
kernel[i] = t;
sum += t;
}

sum = 1 / sum;

for(i = __n; i--;){
kernel[i] *= sum;
}

return kernel;
};

然后通过两个这个一维数组，便可以计算出一个完整的高斯内核，再利用blur里面用到的循环方法，就可以算出高斯平滑后的矩阵了。


代码如下:

function GaussianBlur(__src, __size1, __size2, __sigma1, __sigma2, __borderType, __dst){
if(__src.type && __src.type == "CV_RGBA"){
var height = __src.row,
width = __src.col,
dst = __dst || new Mat(height, width, CV_RGBA),
dstData = dst.data;
var sigma1 = __sigma1 || 0,
sigma2 = __sigma2 || __sigma1;
var size1 = __size1 || Math.round(sigma1 * 6 + 1) | 1,
size2 = __size2 || Math.round(sigma2 * 6 + 1) | 1,
size = size1 * size2;
if(size1 % 2 !== 1 || size2 % 2 !== 1){
console.error("size必须是奇数。");
return __src;
}
var startX = Math.floor(size1 / 2),
startY = Math.floor(size2 / 2);
var withBorderMat = copyMakeBorder(__src, startY, startX, 0, 0, __borderType),
mData = withBorderMat.data,
mWidth = withBorderMat.col;

var kernel1 = getGaussianKernel(size1, sigma1),
kernel2,
kernel = new Array(size1 * size2);

if(size1 === size2 && sigma1 === sigma2)
kernel2 = kernel1;
else
kernel2 = getGaussianKernel(size2, sigma2);

var i, j, c, y, x;

for(i = kernel2.length; i--;){
for(j = kernel1.length; j--;){
kernel[i * size1 + j] = kernel2[i] * kernel1[j];
}
}

var newValue, nowX, offsetY, offsetI;

for(i = height; i--;){
offsetI = i * width;
for(j = width; j--;){
for(c = 3; c--;){
newValue = 0;
for(y = size2; y--;){
offsetY = (y + i) * mWidth * 4;
for(x = size1; x--;){
nowX = (x + j) * 4 + c;
newValue += (mData[offsetY + nowX] * kernel[y * size1 + x]);
}
}
dstData[(j + offsetI) * 4 + c] = newValue;
}
dstData[(j + offsetI) * 4 + 3] = mData[offsetY + startY * mWidth * 4 + (j + startX) * 4 + 3];
}
}

}else{
console.error("不支持的类型");
}
return dst;
}

中值平滑

中值滤波将图像的每个像素用邻域 (以当前像素为中心的正方形区域)像素的

中值代替 。

依然使用blur里面用到的循环，只要得到核中的所有值，再通过sort排序便可以得到中值，然后锚点由该值替代。


代码如下:

function medianBlur(__src, __size1, __size2, __borderType, __dst){
if(__src.type && __src.type == "CV_RGBA"){
var height = __src.row,
width = __src.col,
dst = __dst || new Mat(height, width, CV_RGBA),
dstData = dst.data;
var size1 = __size1 || 3,
size2 = __size2 || size1,
size = size1 * size2;
if(size1 % 2 !== 1 || size2 % 2 !== 1){
console.error("size必须是奇数");
return __src;
}
var startX = Math.floor(size1 / 2),
startY = Math.floor(size2 / 2);
var withBorderMat = copyMakeBorder(__src, startY, startX, 0, 0, __borderType),
mData = withBorderMat.data,
mWidth = withBorderMat.col;

var newValue = [], nowX, offsetY, offsetI;
var i, j, c, y, x;

for(i = height; i--;){
offsetI = i * width;
for(j = width; j--;){
for(c = 3; c--;){
for(y = size2; y--;){
offsetY = (y + i) * mWidth * 4;
for(x = size1; x--;){
nowX = (x + j) * 4 + c;
newValue[y * size1 + x] = mData[offsetY + nowX];
}
}
newValue.sort();
dstData[(j + offsetI) * 4 + c] = newValue[Math.round(size / 2)];
}
dstData[(j + offsetI) * 4 + 3] = mData[offsetY + startY * mWidth * 4 + (j + startX) * 4 + 3];
}
}

}else{
console.error("类型不支持");
}
return dst;
};