GCN 图神经网络使用详解 可视化 Pytorch

目录

• 手动尝试GCN图神经网络
• 现在让我们更详细地看一下底层图
• 现在让我们更详细地检查edge_index的属性
• 嵌入 Karate Club Network
• 训练 Karate Club Network
• 总结

手动尝试GCN图神经网络

最近，图上的深度学习已经成为深度学习社区中最热门的研究领域之一。 在这里，图神经网络（GNN）旨在将经典的深度学习概念推广到不规则的结构化数据（与图像或文本形成对比），并使神经网络能够推理出对象及其关系。

本内容介绍一些关于通过基于PyTorch几何(PyG)库的图神经网络对图进行深度学习的基本概念。

PyTorch geometry是流行的深度学习框架PyTorch的扩展库，由各种方法和实用程序组成，以简化图神经网络的实现。

在开始之前，先介绍一下配置环境：

Pytorch: 1.8.0       Cuda: 10.2    Torch-geometric

# 导入使用的模块包
import torch
import networkx as nx
import matplotlib.pyplot as plt

# 定义最后可视化的函数
def visualize(h, color, epoch=None, loss=None):
    plt.figure(figsize=(7,7))
    plt.xticks([])
    plt.yticks([])

    if torch.is_tensor(h):
        h = h.detach().cpu().numpy()
        plt.scatter(h[:, 0], h[:, 1], s=140, c=color, cmap="Set2")
        if epoch is not None and loss is not None:
            plt.xlabel(f'Epoch: {epoch}, Loss: {loss.item():.4f}', fontsize=16)
    else:
        nx.draw_networkx(G, pos=nx.spring_layout(G, seed=42), with_labels=False,
                         node_color=color, cmap="Set2")
    plt.show()

在这里，我们使用一张KarateClub图来进行讲解，这张图描述了一个由34名空手道俱乐部成员组成的社交网络，并记录了俱乐部外成员之间的联系。在这里，我们感兴趣的是检测由成员的交互产生的社区。

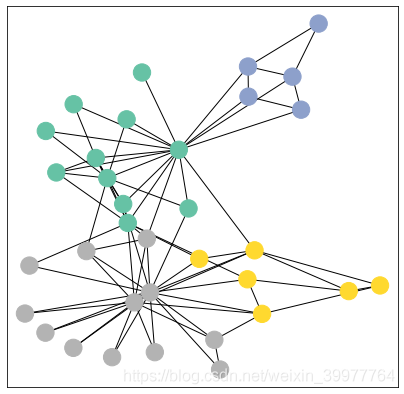
KarateClub图

from torch_geometric.datasets import KarateClub

dataset = KarateClub()
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}') # 1
print(f'Number of features: {dataset.num_features}') # 34
print(f'Number of classes: {dataset.num_classes}') # 4

这里输出的分别是：

• （1）图的数量、
• （2）特征的数量
• （3）种类

在初始化KarateClub数据集之后，我们首先可以检查它的一些属性。

例如，我们可以看到这个数据集只持有一个图，并且这个数据集中的每个节点被分配一个34维的特征向量(唯一地描述空手道俱乐部的成员)。

此外，图中正好包含4个类，它们代表每个节点所属的团体。

现在让我们更详细地看一下底层图

data = dataset[0]  # Get the first graph object.

print(data)
print('==============================================================')

# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
print(f'Contains self-loops: {data.contains_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')

Data(edge_index=[2, 156], train_mask=[34], x=[34, 34], y=[34])
==============================================================
Number of nodes: 34
Number of edges: 156
Average node degree: 4.59
Number of training nodes: 4
Training node label rate: 0.12
Contains isolated nodes: False
Contains self-loops: False
Is undirected: True

PyTorch Geometric 中的每个图形都由单个 Data 对象表示，该对象包含描述其图形表示的所有信息。

我们可以随时通过 print(data) 打印数据对象，以接收有关其属性及其形状的简短摘要：

Data(edge_index=[2, 156], x=[34, 34], y=[34], train_mask=[34])

我们可以看到该数据对象具有4个属性：

（1）edge_index：属性保存有关图连接性的信息，即每个边缘的源节点索引和目标节点索引的元组。 PyG进一步将

（2）节点特征称为x（为34个节点中的每个节点分配了一个34维特征向量），并且将

（3）节点标签称为y（每个节点被精确地分配为一个类别）。

（4）还有一个名为train_mask的附加属性，它描述了我们已经知道其社区归属的节点。 总共，我们只知道4个节点的基本标签（每个社区一个），任务是推断其余节点的社区分配。数据对象还提供一些实用程序功能来推断基础图的某些基本属性。 例如，我们可以轻松推断图中是否存在孤立的节点（即，任何节点都没有边），图是否包含自环（即（v，v）∈E）或图是否为 无向的（即，对于每个边（v，w）∈E也存在边（w，v）∈E）。

现在让我们更详细地检查edge_index的属性

from IPython.display import Javascript  # Restrict height of output cell.
display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 300})'''))

edge_index = data.edge_index
print(edge_index.t())

tensor([[ 0,  1],
        [ 0,  2],
        [ 0,  3],
        [ 0,  4],
        [ 0,  5],
        [ 0,  6],
        [ 0,  7],
        [ 0,  8],
         ........

这个edge_index描述了34个人的相关性。通过输出edge_index，我们可以进一步了解PyG内部是如何表示图连通性的。

我们可以看到，对于每条边，edge_index 包含两个节点索引的元组，其中第一个值描述源节点的节点索引，第二个值描述边的目标节点的节点索引。

这种表示被称为COO格式(坐标格式)，通常用于表示稀疏矩阵。

PyG使用稀疏矩阵代替以密集表示形式的邻接矩阵A∈{0,1} | V |×| V | ，这是指仅保留A中的条目不为零的坐标/值。

我们可以通过将图转换为networkx库格式来进一步可视化，这种格式除了图形操作功能之外，还实现了用于可视化的强大工具

from torch_geometric.utils import to_networkx

G = to_networkx(data, to_undirected=True)
visualize(G, color=data.y)

数据库可视化

灰色、黄色、绿色、蓝色代表四类不同的俱乐部，其中每一个圆圈代表一个人，一共有34个人，每个人之间的关系就如edge_index所描述的那样。

现在，我们要通过在torch.nn.Module类继承中定义我们的网络架构来创建我们的第一个图神经网络

import torch
from torch.nn import Linear
from torch_geometric.nn import GCNConv

class GCN(torch.nn.Module):
    def __init__(self):
        super(GCN, self).__init__()
        torch.manual_seed(12345)
        self.conv1 = GCNConv(dataset.num_features, 4)
        self.conv2 = GCNConv(4, 4)
        self.conv3 = GCNConv(4, 2)
        self.classifier = Linear(2, dataset.num_classes)

    def forward(self, x, edge_index):
        h = self.conv1(x, edge_index)
        h = h.tanh()
        h = self.conv2(h, edge_index)
        h = h.tanh()
        h = self.conv3(h, edge_index)
        h = h.tanh()  # Final GNN embedding space.

        # Apply a final (linear) classifier.
        out = self.classifier(h)

        return out, h

model = GCN()
print(model)

GCN(
  (conv1): GCNConv(34, 4)
  (conv2): GCNConv(4, 4)
  (conv3): GCNConv(4, 2)
  (classifier): Linear(in_features=2, out_features=4, bias=True)
)

在这里，我们首先在 __init__ 中初始化我们所有的构建块，并定义我们forward网络的计算流程。 我们首先定义并堆叠三个图卷积层，这对应于聚合每个节点周围的 3 个邻域信息（所有节点最多 3个）。 此外，GCNConv 层将节点特征维数减少到 2 ，即 34→4→4→2 。 每个 GCNConv 层都通过 tanh 非线性增强。（可以换成RELU试一试）

之后，我们应用单个线性变换 (torch.nn.Linear) 作为分类器将我们的节点映射到 4 个类/社区中的 1 个。

我们返回最终分类器的输出以及GNN生成的最终节点嵌入。 我们继续通过 GCN() 初始化我们的最终模型，打印我们的模型会生成所有使用的子模块的摘要。

嵌入 Karate Club Network

让我们看看GNN产生的节点嵌入。这里，我们将初始节点特征x和图连通性信息edge_index传递给模型，并可视化其二维嵌入。

model = GCN()

_, h = model(data.x, data.edge_index)
print(f'Embedding shape: {list(h.shape)}')

visualize(h, color=data.y)

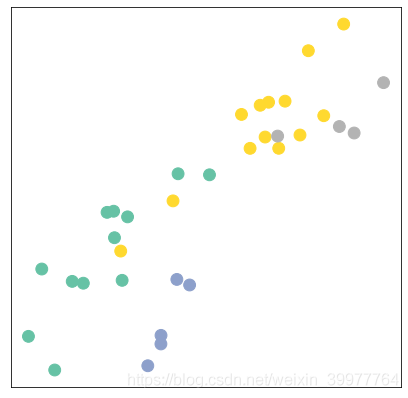
值得注意的是，即使在训练我们的模型的权重之前，该模型也会产生一个与图中的社区结构非常相似的节点嵌入。

相同颜色(社区)的节点在嵌入空间中已经紧密地聚在一起，尽管我们的模型的权值是完全随机初始化的，而且到目前为止我们还没有进行任何训练!由此得出结论，gnn引入了很强的归纳偏置，导致输入图中彼此接近的节点产生类似的嵌入。

训练 Karate Club Network

但我们能做得更好吗？ 让我们看一个示例，说明如何根据图中 4 个节点的社区分配知识（每个社区一个）来训练我们的网络参数：

由于我们模型中的所有内容都是可微分和参数化的，我们可以添加一些标签、训练模型并观察嵌入的反应。 在这里，我们使用半监督或转导学习程序：我们只是针对每个类的一个节点进行训练，但允许使用完整的输入图数据。

这个模型训练与任何其他PyTorch模型非常相似。除了定义我们的网络架构之外，我们还定义了一个损失标准(这里是CrossEntropyLoss)，并初始化了一个随机梯度优化器(这里是Adam)。之后，我们执行多轮优化，每轮由前向和后向传递来计算我们的模型参数w.r.t.对前向传递的损失的梯度。

import time
from IPython.display import Javascript  # Restrict height of output cell.
display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 430})'''))

model = GCN()
criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # Define optimizer.

def train(data):
    optimizer.zero_grad()  # Clear gradients.
    out, h = model(data.x, data.edge_index)  # Perform a single forward pass.
    loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
    loss.backward()  # Derive gradients.
    optimizer.step()  # Update parameters based on gradients.
    return loss, h

for epoch in range(401):
    loss, h = train(data)
    if epoch % 10 == 0:
        visualize(h, color=data.y, epoch=epoch, loss=loss)
        time.sleep(0.3)

可以看到，训练400轮后，它的聚类是比较明显的。正如可以看到的，我们的3层GCN模型管理线性分隔社区和正确分类大多数节点。

此外，我们只用了几行代码就完成了这一切，这要感谢PyTorch geometry库，它帮助我们完成了数据处理和GNN实现。

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。