nlp自然语言处理基于SVD的降维优化学习

目录

• 基于SVD的降维优化
• SVD的直观意义

基于SVD的降维优化

向量降维：尽量保留数据“重要信息”的基础上减少向量维度。可以发现重要的轴（数据分布广的轴），将二维数据 表示为一维数据，用新轴上的投影值来表示各个数据点的值，示意图如下。

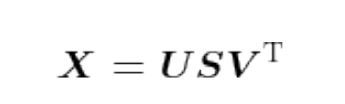
稀疏矩阵和密集矩阵转换：大多数元素为0的矩阵称为稀疏矩阵，从稀疏矩阵中找出重要的轴，用更少的维度对其进行重新表示。结果，稀疏矩阵就会被转化为大多数元素均不为0的密集矩阵。这个密集矩阵就是我们想要的单词的分布式表示。

奇异值分解(Singular Value Decomposition，SVD)：任意的矩阵X分解为U、S、V，3个矩阵的乘积，其中U和V是列向量彼此正交的正交矩阵，S是除了对角线元素以外其余元素均为0的对角矩阵。

关于SVD是怎么回事，从代码中分析：

代码中使用 NumPy 的 linalg 模块中的 svd 方法，如下。

U, S, V = np.linalg.svd(W)

我们输出C、W、U、S、V，如下所示，可以看出，C是共现矩阵、W是PPMI矩阵。可以看到S矩阵是降序排列的。

[0 1 0 0 0 0 0]
[1 0 1 0 1 1 0]
[0 1 0 1 0 0 0]
[0 0 1 0 1 0 0]
[0 1 0 1 0 0 0]
[0 1 0 0 0 0 1]
[0 0 0 0 0 1 0]

[[0.    1.807 0.    0.    0.    0.    0.   ]
 [1.807 0.    0.807 0.    0.807 0.807 0.   ]
 [0.    0.807 0.    1.807 0.    0.    0.   ]
 [0.    0.    1.807 0.    1.807 0.    0.   ]
 [0.    0.807 0.    1.807 0.    0.    0.   ]
 [0.    0.807 0.    0.    0.    0.    2.807]
 [0.    0.    0.    0.    0.    2.807 0.   ]]

[[-3.409e-01 -1.110e-16 -3.886e-16 -1.205e-01  0.000e+00  9.323e-01  2.664e-16]
 [ 0.000e+00 -5.976e-01  1.802e-01  0.000e+00 -7.812e-01  0.000e+00  0.000e+00]
 [-4.363e-01 -4.241e-17 -2.172e-16 -5.088e-01 -1.767e-17 -2.253e-01  -7.071e-01]
 [-2.614e-16 -4.978e-01  6.804e-01 -4.382e-17  5.378e-01  9.951e-17  -3.521e-17]
 [-4.363e-01 -3.229e-17 -1.654e-16 -5.088e-01 -1.345e-17 -2.253e-01  7.071e-01]
 [-7.092e-01 -3.229e-17 -1.654e-16  6.839e-01 -1.345e-17 -1.710e-01  9.095e-17]
 [ 3.056e-16 -6.285e-01 -7.103e-01  7.773e-17  3.169e-01 -2.847e-16  4.533e-17]]

[3.168e+00 3.168e+00 2.703e+00 2.703e+00 1.514e+00 1.514e+00 1.484e-16]

[[ 0.000e+00 -5.976e-01 -2.296e-16 -4.978e-01 -1.186e-16  2.145e-16  -6.285e-01]
 [-3.409e-01 -1.110e-16 -4.363e-01  0.000e+00 -4.363e-01 -7.092e-01  0.000e+00]
 [ 1.205e-01 -5.551e-16  5.088e-01  0.000e+00  5.088e-01 -6.839e-01  0.000e+00]
 [-0.000e+00 -1.802e-01 -1.586e-16 -6.804e-01  6.344e-17  9.119e-17  7.103e-01]
 [-9.323e-01 -5.551e-17  2.253e-01  0.000e+00  2.253e-01  1.710e-01  0.000e+00]
 [-0.000e+00  7.812e-01  2.279e-16 -5.378e-01  3.390e-16 -2.717e-16  -3.169e-01]
 [ 0.000e+00  2.632e-16 -7.071e-01  8.043e-18  7.071e-01  9.088e-17  1.831e-17]]

下面研究U、S、V矩阵究竟是什么，添加如下代码。

print("______________________")
jym = np.dot(V, U)
print(jym)
print("______________________")
jym2 = np.dot(U, V)
print(jym2)
print("______________________")
V2 = np.transpose(V)
jb = np.dot(V, V2)
print(jb)

输出如下，那就可以把U和V的性质给搞懂了。从jb = np.dot(V, V2)，输出jb矩阵是单位矩阵，可知，V和U是正交矩阵。jym = np.dot(V, U)，输出jym主对角线元素全为0。U和V是列向量彼此正交的，公式里面把V转置了也就是说，U的列向量和代码里的V的行向量是正交的，所以用V乘U，他们的对角元是0。

[[-6.212e-17  1.000e+00  1.015e-08  2.968e-16 -5.249e-09  1.712e-16  6.754e-17]
 [ 1.000e+00  1.597e-16  3.967e-16 -2.653e-08  1.099e-16 -1.336e-08  -5.293e-09]
 [ 2.653e-08  3.025e-16 -2.284e-16 -1.000e+00  4.270e-16  1.110e-08  5.760e-09]
 [ 3.718e-16 -1.015e-08 -1.000e+00  1.958e-16  4.416e-10 -2.641e-16  2.132e-16]
 [ 1.336e-08  1.143e-16  2.378e-16  1.110e-08  3.405e-17 -1.000e+00  -2.662e-09]
 [-1.096e-17  5.249e-09  4.416e-10 -4.753e-16 -1.000e+00 -4.458e-17  8.307e-17]
 [-5.293e-09 -1.657e-16  7.657e-17 -5.760e-09 -1.925e-16  2.662e-09  1.000e+00]]

[[-8.977e-18  9.539e-01 -2.775e-17 -2.497e-01  3.879e-16  7.108e-18  -1.668e-01]
 [ 9.539e-01  9.667e-18  1.764e-01  0.000e+00  1.764e-01  1.670e-01  0.000e+00]
 [ 4.757e-18  1.764e-01  5.000e-01  6.846e-01 -5.000e-01  3.262e-17  -1.578e-02]
 [-2.497e-01 -1.105e-16  6.846e-01  1.064e-16  6.846e-01 -2.032e-02  1.016e-16]
 [ 3.622e-18  1.764e-01 -5.000e-01  6.846e-01  5.000e-01  1.192e-16  -1.578e-02]
 [ 3.622e-18  1.670e-01 -1.220e-16 -2.032e-02  6.079e-17  9.043e-17  9.857e-01]
 [-1.668e-01  2.741e-17 -1.578e-02 -5.192e-17 -1.578e-02  9.857e-01  -4.663e-17]]

[[ 1.000e+00  6.620e-17  7.901e-18 -1.015e-08 -8.632e-18  5.249e-09  -9.431e-17]
 [ 6.620e-17  1.000e+00  2.653e-08 -3.141e-18  1.336e-08 -1.414e-16  -5.293e-09]
 [ 7.901e-18  2.653e-08  1.000e+00 -1.074e-17 -1.110e-08  4.054e-17  5.760e-09]
 [-1.015e-08 -3.141e-18 -1.074e-17  1.000e+00  4.150e-18 -4.416e-10  1.171e-16]
 [-8.632e-18  1.336e-08 -1.110e-08  4.150e-18  1.000e+00  3.792e-17  -2.662e-09]
 [ 5.249e-09 -1.414e-16  4.054e-17 -4.416e-10  3.792e-17  1.000e+00  2.740e-16]
 [-9.431e-17 -5.293e-09  5.760e-09  1.171e-16 -2.662e-09  2.740e-16  1.000e+00]]

SVD的直观意义

U是正交矩阵。这个正交矩阵构成了一些空间中的基轴 （基向量），可以将矩阵U作为“单词空间”。 S是对角矩阵，奇异值在对角线上降序排列，奇异值的大小也就意味着“对应的基轴”的重要性。奇异值小，对应基轴重要性就小，所以可以通过去除U矩阵中的多余的列向量来近似原始矩阵。从而把单词向量用降维后的矩阵表示。示意图如下。

稀疏向量W经过 SVD 被转化成了密集向量U。如果要对这个密集向量降维，比如把它降维到二维向量，取出U的前两个元素即可。

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(id_to_word)
C = create_co_matrix(corpus, vocab_size, window_size=1)
W = ppmi(C)
# SVD
U, S, V = np.linalg.svd(W)
np.set_printoptions(precision=3)  # 有效位数为3位
for i in range(7):
    print(C[i])
print(U)
# plot
for word, word_id in word_to_id.items():
    plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()

输出的U：

[[-3.409e-01 -1.110e-16 -3.886e-16 -1.205e-01  0.000e+00  9.323e-01
   2.664e-16]
 [ 0.000e+00 -5.976e-01  1.802e-01  0.000e+00 -7.812e-01  0.000e+00
   0.000e+00]
 [-4.363e-01 -4.241e-17 -2.172e-16 -5.088e-01 -1.767e-17 -2.253e-01
  -7.071e-01]
 [-2.614e-16 -4.978e-01  6.804e-01 -4.382e-17  5.378e-01  9.951e-17
  -3.521e-17]
 [-4.363e-01 -3.229e-17 -1.654e-16 -5.088e-01 -1.345e-17 -2.253e-01
   7.071e-01]
 [-7.092e-01 -3.229e-17 -1.654e-16  6.839e-01 -1.345e-17 -1.710e-01
   9.095e-17]
 [ 3.056e-16 -6.285e-01 -7.103e-01  7.773e-17  3.169e-01 -2.847e-16
   4.533e-17]]

用二维向量表示各个单词，并把它们画在图上，画出的图如下：goodbye 和 hello、you 和 i 位置接近，这个结果复合之前做的基于余弦相似度的结果。

以上就是nlp自然语言处理基于SVD的降维优化学习的详细内容，更多关于nlp自然语言处理SVD的降维优化的资料请关注我们其它相关文章！