Java实现最小高度树

目录

• 题设要求
• 示例 1：
• 示例 2：
• 解题思路
• 算法

题设要求

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

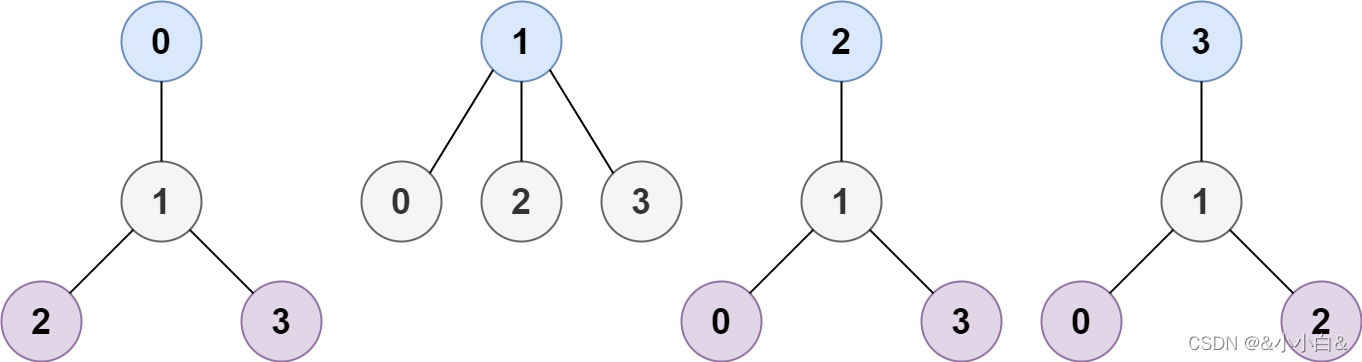
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

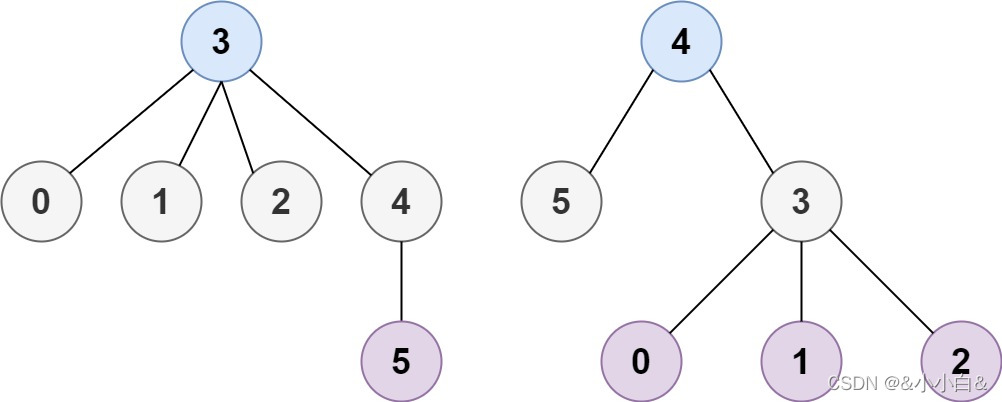
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

提示：
1 <= n <= 2 * 104
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入保证是一棵树，并且不会有重复的边

解题思路

​  由上述两个图我们可以得出结论：题中需要求解的是树里面的中心节点，而每个树的中心节点不会超过两个。

​  而我们想要求得树里面的中心节点，我们就可以逐层FBS（也就是逐层将出度为一的叶子节点剪掉），直至剪到最后一层，就可以将结果输出了！

算法

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> res = new ArrayList<Integer>();
        //如果只有一个节点，则它就是最小高度树
        if(n == 1){
            res.add(0);
            return res;
        }

        //每个节点的邻居数量
        int [] degree = new int[n];
        //每个节点的邻居
        HashMap<Integer,List<Integer>> map = new HashMap<>();

        for(int [] edge : edges){
            int a = edge[0];
            int b = edge[1];

            degree[a]++;
            degree[b]++;

            if(map.get(a) == null){
                map.put(a,new ArrayList<Integer>());//key:节点   value:邻居
            }

            if(map.get(b) == null){
                map.put(b,new ArrayList<Integer>());//key:节点   value:邻居
            }

            map.get(a).add(b);
            map.get(b).add(a);
        }

        //建立队列
        LinkedList<Integer> leafNodes = new LinkedList<Integer>();//表示叶子节点
        //将所有度为1的节点入队
        for(int i = 0;i < degree.length;i++){
            if(degree[i] == 1){
                leafNodes.add(i);
            }
        }

        while(leafNodes.size() > 0){
            res.clear();
            //每一层节点的数量
            int size = leafNodes.size();

            for(int i = 0;i < size;i++){
                int leaf = leafNodes.poll();
                //将当前节点加入到结果集
                res.add(leaf);

                List<Integer> neighbors = map.get(leaf);
                //将出度减一，也就是将最外层的叶子节点剪掉
                for(int neighbor : neighbors){
                    degree[neighbor]--;
                    if(degree[neighbor] == 1){
                        //叶子节点入队
                        leafNodes.add(neighbor);
                    }
                }
            }
        }
        return res;
    }
}

到此这篇关于Java实现最小高度树的文章就介绍到这了,更多相关Java 最小高度树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！