Python使用scipy保存图片的一些注意点

首先我们载入一张灰度图片，一般灰度图片像素为0-255.

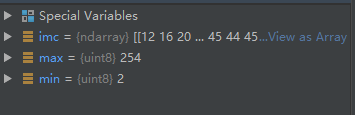
可以发现该图片的最大像素为254，最小像素为2。一般处理图片时会转化为double类型。

我们将图片使用scipy保存为pgm格式。

然后我们重新读取该图片信息。

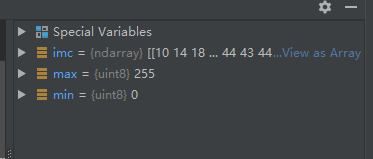
其像素值发生了变化，自动标准化到了0-255范围，最小值变为0，最大值变为255.

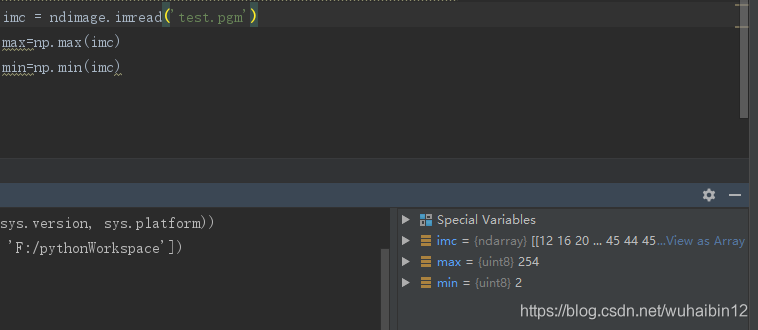
所以，使用scipy保存图像时，加上2个参数，cmin和cmax。就可以了

重新读取图片。结果正确

补充：from scipy import misc 读取和保存图片

from scipy import misc

def imread(name, flatten=False, mode=None)
    pass
"""
读取一张图片返回array，uint8，"""
def imsave(name, arr, format=None):
    pass
"""
Save an array as an image. 自动的调用将图片转成0-255范围内的
arr : ndarray, MxN or MxNx3 or MxNx4
        Array containing image values.  If the shape is ``MxN``, the array
        represents a grey-level image.  Shape ``MxNx3`` stores the red, green
        and blue bands along the last dimension.  An alpha layer may be
        included, specified as the last colour band of an ``MxNx4`` array.
"""

注意上面对图片读取和保存的函数会被弃用，使用如下代替：

import imageio
imageio.imread()
imageio.imwrite()

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python 读取图片文件为矩阵和保存矩阵为图片的方法

    读取图片为矩阵 import matplotlib im = matplotlib.image.imread('0_0.jpg') 保存矩阵为图片 import numpy as np import scipy x = np.random.random((600,800,3)) scipy.misc.imsave('meelo.jpg', x) 以上这篇Python 读取图片文件为矩阵和保存矩阵为图片的方法就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持我们. 您可能感兴

  • python读取和保存图片5种方法对比

    python读取和保存图片5种方法对比 python中对象之间的赋值是按引用传递的,如果需要拷贝对象,需要用到标准库中的copy模块 方法一:利用 PIL 中的 Image 函数 这个函数读取出来不是 array 格式,这时候需要用 np.asarray(im) 或者 np.array()函数 . 区别:np.array() 是深拷贝,np.asarray() 是浅拷贝 copy.copy 浅拷贝 只拷贝父对象,不会拷贝对象的内部的子对象. copy.deepcopy 深拷贝 拷贝对象及其子对象

  • 浅谈python下tiff图像的读取和保存方法

    对比测试 scipy.misc 和 PIL.Image 和 libtiff.TIFF 三个库 输入: 1. (读取矩阵) 读入uint8.uint16.float32的lena.tif 2. (生成矩阵) 使用numpy产生随机矩阵,float64的mat import numpy as np from scipy import misc from PIL import Image from libtiff import TIFF # # 读入已有图像,数据类型和原图像一致 tif32 = mi

  • Python使用scipy保存图片的一些注意点

    Python使用scipy保存图片的一些注意点

    首先我们载入一张灰度图片,一般灰度图片像素为0-255. 可以发现该图片的最大像素为254,最小像素为2.一般处理图片时会转化为double类型. 我们将图片使用scipy保存为pgm格式. 然后我们重新读取该图片信息. 其像素值发生了变化,自动标准化到了0-255范围,最小值变为0,最大值变为255. 所以,使用scipy保存图像时,加上2个参数,cmin和cmax.就可以了 重新读取图片.结果正确 补充:from scipy import misc 读取和保存图片 from scipy im

  • 浅谈python中scipy.misc.logsumexp函数的运用场景

    scipy.misc.logsumexp函数的输入参数有(a, axis=None, b=None, keepdims=False, return_sign=False),具体配置可参见这里,返回的值是np.log(np.sum(np.exp(a))). 这里需要强调的是使用该函数的场景: 一般来说,该函数主要用于非常小的数值的运算(比如蒙特卡洛取样样本).在这种情况下,将数据保持log处理是必须的.所以这时你如果想将数组中的数据累加求和就需要这样计算log(sum(exp(a))),但这样做就

  • 解决Python plt.savefig 保存图片时一片空白的问题

    更新 这里我会列出对本文的更新. 2017 年 9 月 28 日:修正几处错字,优化排版. 问题 当使用如下代码保存使用 plt.savefig 保存生成的图片时,结果打开生成的图片却是一片空白. import matplotlib.pyplot as plt """ 一些画图代码 """ plt.show() plt.savefig("filename.png") 原因 其实产生这个现象的原因很简单:在 plt.show()

  • Python基于scipy实现信号滤波功能

    Python基于scipy实现信号滤波功能

    ​ 1.背景介绍 在深度学习中,有时会使用Matlab进行滤波处理,再将处理过的数据送入神经网络中.这样是一般的处理方法,但是处理起来却有些繁琐,并且有时系统难以运行Matlab.Python作为一种十分强大的语言,是支持信号滤波滤波处理的. 本文将以实战的形式基于scipy模块使用Python实现简单滤波处理,包括内容有1.低通滤波,2.高通滤波,3.带通滤波,4.带阻滤波器.具体的含义大家可以查阅大学课程,信号与系统.简单的理解就是低通滤波指的是去除高于某一阈值频率的信号:高通滤波去除低于某

  • python安装scipy的方法步骤

    python安装scipy的方法步骤

    Scipy高级科学计算库:和Numpy联系很密切,Scipy一般都是操控Numpy数组来进行科学计算.统计分析,所以可以说是基于Numpy之上了. Scipy库的安装 pip install scipy Scipy有很多子模块可以应对不同的应用,例如插值运算,优化算法等等.SciPy则是在NumPy的基础上构建的更为强大,应用领域也更为广泛的科学计算包.正是出于这个原因,SciPy需要依赖NumPy的支持进行安装和运行. SciPy是世界上著名的Python开源科学计算库,建立在Numpy之上.

  • Python使用scipy模块实现一维卷积运算示例

    本文实例讲述了Python使用scipy模块实现一维卷积运算.分享给大家供大家参考,具体如下: 一 介绍 signal模块包含大量滤波函数.B样条插值算法等等.下面的代码演示了一维信号的卷积运算. 二 代码 import numpy as np import scipy.signal x = np.array([1,2,3]) h = np.array([4,5,6]) print(scipy.signal.convolve(x, h))#一维卷积运算 三 运行结果 [ 4 13 28 27 1

  • python中scipy.stats产生随机数实例讲解

    python的numpy 能生成一定概率分布的随机数,但如果需要更具体的概率密度,累积概率,就要使用scipy.stats.scipy.stats用于统计分析,统计工具和随机过程的概率,各个随机过程的随机数生成器可以从numpy.random中找到.本文介绍python中使用scipy.stats产生随机数的原理及实例. 1.scipy.stats正态分步格式 scipy.stats #生成指定分布 scipy.stats.poisson.rvs(loc=期望, scale=标准差, size=

  • python的scipy.stats模块中正态分布常用函数总结

    python的scipy.stats模块是连续型随机变量的公共方法,可以产生随机数,通常是以正态分布作为scipy.stats的基本使用方法.本文介绍正态分布的两种常用函数:1.累积概率密度函数stats.norm.cdf(α,均值,方差):2.概率密度函数stats.norm.pdf(α,均值,方差). 1.stats.norm.cdf(α,均值,方差):累积概率密度函数 使用格式 status.norm.cdf(Norm) # 相当于已知正态分布函数曲线和x值,求函数x点左侧积分 使用实例

  • Python使用scipy.fft进行大学经典的傅立叶变换

    Python使用scipy.fft进行大学经典的傅立叶变换

    傅里叶变换是在高数是一个很重要的知识点,今天将结合Python代码实现傅立叶变换. 傅立叶变换 我们平时是如何去分解一个复杂的问题呢?一个经典的方法就是把这个复杂的问题分解成为多个简单的可操作的子问题, 傅立叶变换也是基于这个思想. 傅里叶分析是研究如何将数学函数分解为一系列更简单的三角函数的领域.傅里叶变换是该领域的一种工具,用于将函数分解为其分量频率. 在本教程中,傅立叶变换是一种工具,可以获取信号并查看其中每个频率的功率.看一看该傅立叶变换中的重要术语: 信号:信号是随时间变化的信息.例如

随机推荐