Python与C++中梯度方向直方图的实现

目录

• 什么是特征描述子
• 如何计算梯度方向直方图
• Step1:预处理
• Step2:计算梯度图
• Step3:在8×8的cell中计算梯度直方图
• Step4:16×16Block标准化
• Step5:计算HOG特征向量
• 梯度直方图可视化

原文链接：Histogram of Oriented Gradients

(文中的图片均来自翻译原文)

什么是特征描述子

特征描述子一张图片或者一个图片块的一种表示，通过提取有用信息并扔掉多余的信息来简化图像。

通常，特征描述子将一张大小为width×height×3 (通道数)的图片化成一个长度为n的特征向量/数组。以HOG特征为例，输入图像的大小是64×128×3，输出是一个长度为3780的特征向量。

注意一点，HOG特征也可以是其它大小，但这里我使用原文献中使用的大小，这样你可以更容易地通过一个具体的例子来理解这个概念。

上面这些听起来不错，但是对于一张图片的信息，哪些是有用的哪些是冗余的呢？为了定义这个有用信息，我们需要知道它对什么有用。显然，特征向量对于我们看一张图像没什么用。但是，它对图像识别和目标检测这样的任务很有用。将由这些算法生成的特征向量作为支持向量机等分类算法的输入往往可以得到不错的结果。

但是，对于分类任务来说，哪类特征是有用的呢？让我们先用一个例子讨论一下。假设我们想设计一个目标检测器来检测衬衫或者外套上的纽扣。通常纽扣是圆的（可能在图片上会是椭圆）而且一般会有一些孔用于缝纫。你可以在一张纽扣的图片上执行边缘检测，仅仅通过观察边缘图像就可以判断它是不是一个纽扣。在这个例子中，边缘信息是有用的而颜色信息是无用的。此外，特征也需要有区分能力。例如，从某一张图片中提取的一个好的特征应具备区分纽扣和其他圆心物体（如硬币和车轮）的能力。

对于HOG特征描述子，选用梯度方向的分布作为特征。一张图像的梯度（x和y方向的导数）很有用因为在边缘和拐角（强度变化剧烈的区域）处的梯度幅值很大。而且我们知道边缘和拐角比其他平坦的区域包含更多关于物体形状的信息。

如何计算梯度方向直方图

在这一节，我们将详细介绍HOG描述子的计算。为了解释计算的每个步骤，我们使用一个图片块进行分析。

Step 1: 预处理

正像之前提到的那样，HOG特征通过在一张64×128的图片块上计算得到以用于行人检测。当然完整的图片可以是任意的尺寸。通常我们会在图片的不同位置分析多尺度图片块。唯一的要求就是图片块需要有固定的长宽比。在我们的例子中，图片块需要保持1：2 的纵横比。比如：100×200， 128×256或者1000×2000都可以，但101×205就不满足要求。

为了解释这一点，我在下面选用了一张720×475的图片。我们在图上选择一个图片块来计算HOG特征。这个小块是从原图像上裁剪下来的并且纵横比调整为64×128。这样我们就准备好计算这个图片块的HOG特征了。

原始文献中Dalal和Triggs也将 γ γ 矫正放在预处理步骤中，但是带来的增益很小因此这里我们忽略这一步。

Step 2: 计算梯度图

为了计算HOG特征，我们需要先计算图像水平和竖直方向的梯度。毕竟我们想要计算梯度直方图。这一步可以很容易通过的核对对原图像进行滤波实现。

我们也可以使用OpenCV中的Sobel算子（kernel size设为1）得到相同的结果。

// C++ gradient calculation.
// Read image
Mat img = imread("bolt.png");
img.convertTo(img, CV_32F, 1/255.0);

// Calculate gradients gx, gy
Mat gx, gy;
Sobel(img, gx, CV_32F, 1, 0, 1);
Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation 

# Read image
im = cv2.imread('bolt.png')
im = np.float32(im) / 255.0

# Calculate gradient
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

下一步我们可以用下面的公式来计算梯度的幅值和方向。

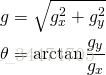
如果你使用OpenCV，可以通过下面的cartToPolar函数实现。

// C++ Calculate gradient magnitude and direction (in degrees)
Mat mag, angle;
cartToPolar(gx, gy, mag, angle, 1); 

在Python中实现如下：

# Python Calculate gradient magnitude and direction ( in degrees )
mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

下图显示了计算得到的梯度：

左：X方向梯度幅值图；中：Y方向梯度幅值图；右：梯度幅值图

X方向的梯度凸显竖直的线而Y方向的梯度凸显水平的线。梯度的幅值出现在强度变化剧烈的地方。在强度平坦的区域几乎没有梯度。我故意忽略了梯度方向图，因为在图像上显示梯度方向没有传递太多的信息。

梯度图像移除了很多不必要的信息（比如不变的背景），突出了轮廓信息。也就是说，你仅仅通过看梯度图像还是可以辨认出图像有有一个人。

对于每一个像素，梯度都会有幅值和方向。对于彩色图像，需要分别计算3个通道的梯度（如上图所示）。而该像素点的幅值是这3个通道梯度幅值的最大值，方向是最大梯度幅值对应的角度。

Step 3: 在8×8的cell中计算梯度直方图

在这一步，图像被分成8×8的很多cell，而梯度直方图是在这些cell中计算出来的。

我们一会儿将学习直方图，但在那之前，我们先理解一下为什么将图像切分成很多8×8的cell。使用特征描述子来描述图像中的一小块的一个重要原因是它用更为紧凑的表示方法刻画了原图像。一个8×8的图片块包含了8×8×3=192个像素值。而这个图像块的每个像素点梯度信息包含梯度幅值和方向两个值，一共是8×8×2=128个值，这128个值可以通过用包含9个bin的直方图表示成一个一维数组（包含9个值）。这样做不仅可以使图像表示更紧凑，而且在一个图片块中计算直方图可以让这种表示方法对噪声有更强的鲁棒性。单个像素的梯度信息可能包含噪声，而一个8×8的图片块中的直方图让这种表示方法对噪声更不敏感。

但是为什么要用8×8的图片块呢？为什么不是32×32？这是由我们需要寻找的特征比例决定的。HOG特征起初是被用来检测行人的。8×8的cell在一张64×128的行人图片块中的足以捕捉感兴趣的特征（如人脸、头顶等）。

上述梯度直方图本质上是一个包含9个数字的向量（或数组），这9个数字分别对应0°、20°、40°、… 160°。

我们来看一下图片块中的一个8×8 cell的梯度是什么样子。

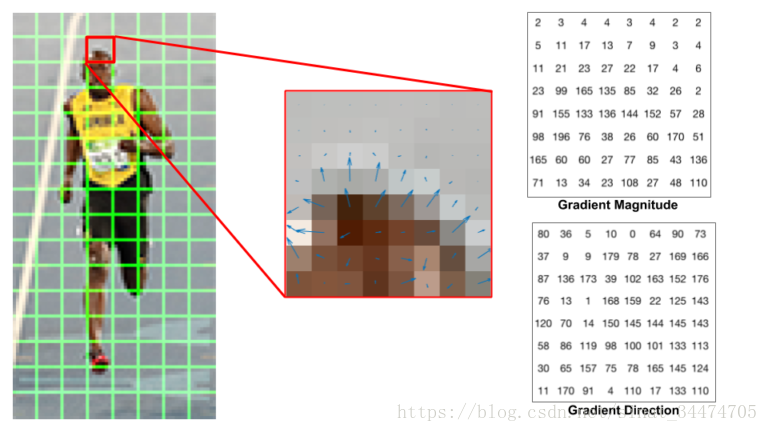
中：一个RGB cell及其梯度（用箭头表示）；右：cell中的梯度大小和方向（数字表示）

如果你是一个计算机视觉领域新手，中间的这幅图为你提供了很多信息。它展示了用箭头表示的梯度信息的梯度图——箭头的指向表示了梯度的方向而箭头的长度表示了梯度的大小。需要注意到的一点是箭头的方向指向了图像强度变化的方向，而梯度大小表示了强度的变化有多大。

在右边的图上，我们发现8×8的cell中表示梯度的数字有一点细微的差别——角度实在0°到180°之间的而不是0°到360°之间。这些叫做“无符号梯度”，因为因为一个正负方向的两个梯度由同一个数字表示。换句话说，某一个梯度箭头和它对应的另一个值（加上180°对应的那个值）被当作是同一个梯度。根据经验，无符号梯度被证明比有符号梯度效果更好。一些HOG特征的实现代码会允许你选择是否使用有符号梯度。

下一步就是在这些8×8的cells上创建梯度直方图。直方图包含9个bins分别对应着0°、20°、40°、… 160°。

下图解释了具体的过程。我们在和上面那个图一样的8×8的cells上查看梯度的大小和方向。每个bin是基于梯度方向选出来的，对应的票数（加在当前bin上的值）对应着梯度的大小。我们先来看看用蓝色圆圈出来的像素，它的梯度的角度是80°，大小为2。因此它在第5个bin上加2。下图中用红色圈出来的梯度的角度是10°，大小是4。由于10°是在0°和20°的中间位置， 因此改位置梯度对应票数被一分为二加到相邻的两个bin上。

还有一个细节需要注意。如果梯度方向大于160°。此时梯度的角度位于160°和180°之间。我们知道0°和180°是一样的（无符号梯度），因此在下面的例子中，梯度方向为165°的像素按比例将梯度大小分配到0°和160°的bin中。

8×8的cell中所有像素处的梯度按照方向将梯度大小累加到9个bin以创建最后的梯度直方图。上图中的cell对应的梯度直方图如下：

在我们的表示结果中，y轴对应0°。你可以发现上面的直方图中有大量的权重（梯度大小的投票结果）在0°和180°附近，这从另外一个角度说明了在这个cell中大部分梯度方向要么朝上要么朝下。

Step 4: 16×16 Block标准化

在上述步骤中，我们基于图像的梯度创建直方图。一张图片的梯度对整体的光线的光线比较敏感。如果你把图像所有的像素值除以2使整张图像变暗，梯度的大小也会变为原来的一半，从而梯度直方图的值也会将为原来的一半。理想情况下，我们想让特征描述子独立于光线变化。换句话说，我们想要“标准化”这个直方图使它不受光线变化的影响。

在我讲梯度直方图如何标准化之前，我们先来看看一个长度为3的向量如何标准化。

假设我们有一个RGB颜色向量[128, 64, 32]。这个向量的长度是

。这也叫做向量的L2范数。将这个向量的所有元素除以向量长度146.64就可以得到一个标准化的向量[0.87, 0.43, 0.22]，现在考虑另外一个向量，这个向量的元素是第一个向量的两倍即2×[128, 64, 32]=[256, 128, 64]。你可以自己计算一下它对应的标准化结果，发现结果仍然是[0.87, 0.43, 0.22]，这个值和第一个RGB向量的标准化向量相同。你可以发现标准化一个向量移除了这个向量的尺度信息。

现在我们知道如何标准化一个向量，你可能想到当计算HOG特征的时候你可以像之前标准化一个3×1向量一样去标准化9×1的直方图。这的确是个不错的想法，但是更好的做法是标准化一个更大的16×16的block。一个16×16的block包含4个直方图，这4个直方图可以连接成一个36×1的向量，而且这个向量仍然可以像那个3×1的向量一样进行标准化。每次标准化后，整个窗口移动8个像素并再次计算得到一个36×1的标准化向量，就这样一直重复这个过程。

Step 5: 计算HOG特征向量

为了计算整个图片块最终的特征向量所有的36×1的向量被连接成一个大向量。这个大向量的维度是多少大呢？

我们来计算： - 1. 我们有多少个不同位置的16×16的block？一共有 (64-8)/8=7 个水平的位置和 (128-8)/8=15 个竖直的位置，所以总计7×15=105个。 - 2. 每一个16×16的block被表示成一个36×1的向量。因此，当我们把他们连接成一个大向量的时候会得到一个36×105=3780维度的向量。

梯度直方图可视化

一个图像块梯度特征的可视化通常通过在所有8×8的cell里画出对应的标准化的9×1向量（直方图）。如下图所示。你会注意到直方图的主要方向捕捉了人的形状，尤其是在躯干和腿附近。

不幸的是，目前在OpenCV中并没有一个简单的方法方法来可视化HOG特征。

到此这篇关于Python与C++中梯度方向直方图的实现的文章就介绍到这了,更多相关Python 梯度方向直方图内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！