JAVA十大排序算法之希尔排序详解

目录

• 希尔排序
• 代码实现
• 时间复杂度
• 算法稳定性
• 总结

希尔排序

一种基于插入排序的快速的排序算法。简单插入排序对于大规模乱序数组很慢，因为元素只能一点一点地从数组的一端移动到另一端。例如，如果主键最小的元素正好在数组的尽头，要将它挪到正确的位置就需要n-1次移动。

希尔排序为了加快速度简单地改进了插入排序，也称为缩小增量排序。

希尔排序是把待排序数组按一定的数量分组，对每组使用直接插入排序算法排序；然后缩小数量继续分组排序，随着数量逐渐减少，每组包含的元素越来越多，当数量减至 1 时，整个数组恰被分成一组，排序便完成了。这个不断缩小的数量，就构成了一个增量序列，这里的数量称为增量。

代码实现

public class ShellSort {

    public static final int[] ARRAY = {12, 9, 6, 11, 5, 1, 14, 2, 10, 4, 8, 7, 13, 3};

    public static int[] sort(int[] array) {
        int len = array.length;
        if (len < 2) {
            return array;
        }
        //当前待排序数据，该数据之前的已被排序
        int current;
        //增量
        int gap = len / 2;
        while (gap > 0) {
            for (int i = gap; i < len; i++) {
                current = array[i];
                //前面有序序列的索引
                int index = i - gap;
                while (index >= 0 && current < array[index]) {
                    array[index + gap] = array[index];
                    //有序序列的下一个
                    index -= gap;
                }
                //插入
                array[index + gap] = current;
            }
            //int相除取整
            gap = gap / 2;
        }
        return array;
    }

    public static void print(int[] array) {
        for (int i : array) {
            System.out.print(i + "  ");
        }
        System.out.println("");
    }

    public static void main(String[] args) {
        print(ARRAY);
        System.out.println("============================================");
        print(sort(ARRAY));
    }
}

时间复杂度

希尔排序的复杂度和增量序列有关。

在先前较大的增量下每个子序列的规模都不大,用直接插入排序效率都较高，尽管在随后的增量递减分组中子序列越来越大,由于整个序列的有序性也越来越明显,则排序效率依然较高。

从理论上说，只要一个数组是递减的，并且最后一个值是1，都可以作为增量序列使用。有没有一个步长序列,使得排序过程中所需的比较和移动次数相对较少,并且无论待排序列记录数有多少,算法的时间复杂度都能渐近最佳呢？但是目前从数学上来说，无法证明某个序列是最好的。

常用的增量序列：

• 希尔增量序列 ：{n/2, (n / 2)/2, …, 1}，其中N为原始数组的长度，这是最常用的序列，但却不是最好的
• Hibbard序列：{2k-1, …, 3,1}
• Sedgewick序列：{… , 109 , 41 , 19 , 5，1} 表达式为9 * 4i- 9 * 2i + 1，i = 0，1，2，3，4…

算法稳定性

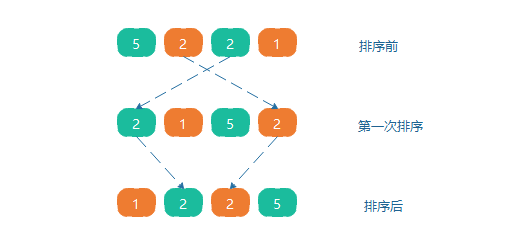
由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，如数组5，2，2，1，第一次排序第一个元素5会和第三个元素2交换，第二个元素2会和第四个元素1交换，原序列中两个2的相对前后顺序就被破坏了，所以希尔排序是一个不稳定的排序算法。

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容!