Python深度学习理解pytorch神经网络批量归一化

目录

• 训练深层网络
• 为什么要批量归一化层呢？
• 批量归一化层
• 全连接层
• 卷积层
• 预测过程中的批量归一化
• 使用批量归一化层的LeNet
• 简明实现
• 争议

训练深层神经网络是十分困难的，特别是在较短的实践内使他们收敛更加棘手。在本节中，我们将介绍批量归一化（batch normalization），这是一种流行且有效的技术，可持续加速深层网络的收敛速度。在结合之后将介绍的残差快，批量归一化使得研究人员能够训练100层以上的网络。

训练深层网络

为什么要批量归一化层呢？

让我们回顾一下训练神经网络时出现的一些实际挑战：

1.数据预处理的方式通常会对最终结果产生巨大影响。回想一下我们应用多层感知机来预测房价的例子。使用真实数据时，我们的第一步是标准化输入特征，使其平均值为0，方差为1。直观地说，这种标准化可以很好地与我们地优化器配合使用，因为它可以将参数的量级进行统一。

2.对于典型的多层感知机或卷积伸进网络。当我们训练时，中间层中的变量（例如，多层感知机中的仿射变换输出）可能具有更广的变化范围：不论是沿着从输入到输出的层，跨同一层中的单元，或是随着时间的推移，模型的参数随着训练更新变幻莫测。批量归一化的发明者非正式地假设，这些变量分布中的这种偏移可能会阻碍网络的收敛。直观地说，我们可能会猜想，如果一个层的可变值是另一层的100倍，这可能需要对学习率进行补偿调整。

3.更深层的网络很复杂，容易过拟合。这意味着正则化变得更加需要。

批量归一化应用于单个可选层（也可以应用到所有层），其原理如下：
在每次训练迭代中，我们首先归一化输入，即通过减去其平均值并除以其标准差，其中两者均基于当前小批量处理。
接下来，我们应用比例系数和比例偏移。
正是由于这个基于批量统计的标准化，才有了批量标准化的名称。

这里，如果我们尝试使用大小为1的小批量应用小批量归一化，我们将无法学到任何东西。这是因为在减去均值之后，每个隐藏单元将为0。所以，只有使用足够大的小批量，批量归一化这种方法才是有效且稳定的。请注意，在应用批量归一化时，批量大小的选择可能比没有批量归一化时更重要。

现在，我们了解一下批量归一化在实践中是如何工作的。

批量归一化层

回想一下，批量归一化和其他图层之间的一个关键区别是，由于批量归一化在完整的小批次上运行，因此我们不能像以前在引入其他图层时忽略批处理的尺寸大小。我们在下面讨论这两种情况：全连接层和卷积层，它们的批量归一化实现略有不同。

全连接层

通常，我们将批量归一化层置于全连接层中的仿射变换和激活函数之间。

卷积层

同样，对于卷积层，我们可以在卷积层之后和非线性激活函数之前应用批量归一化。当卷积有多个输出通道时，我们需要对这些通道的“每个”输出执行批量归一化，每个用到都有自己的拉伸和偏移参数，这两个参数都是标量。假设我们的微批次包含 m m m个示例，并且对于每个通道，卷积的输出具有高度 p p p和宽度 q q q。那么对于卷积层，我们在每个输出通道的 m ∗ p ∗ q m*p*q m∗p∗q个元素上同时执行每个批量归一化。因此，在计算平均值和方差时，我们会收集所有空间位置的值，然后在给定通道内应用相同的均值和方差，以便在每个空间位置对值进行归一化。

预测过程中的批量归一化

正如我们前面提到的，批量归一化在训练模式和预测模式下的行为通常是不同的。
首先，将训练好的模型用于预测时，我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了。
其次，例如，我们可能需要使用我们的模型对逐个样本进行预测。一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。可见，和dropout一样，批量归一化层在训练模式和预测模式下的计算结果也是不一样的。

使用批量归一化层的LeNet

为了更好理解如何应用BatchNorm，下面我们将其应用于LeNet模型。回想一下，批量归一化是在卷积层或全连接层之后、相应的激活函数之前应用的。

net = nn.Sequential(
	nn.Conv2d(1, 6, kernel_size = 5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
	nn.MaxPool2d(kernel_size=2, stride=2)
	nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
	nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
	nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
	nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
	nn.Linear(84, 10)
)

和以前一样，我们将在Fashion-MNIST数据集上训练网络。这个代码与我们第一次训练LeNet时几乎完全相同，主要区别在于学习率大得多。

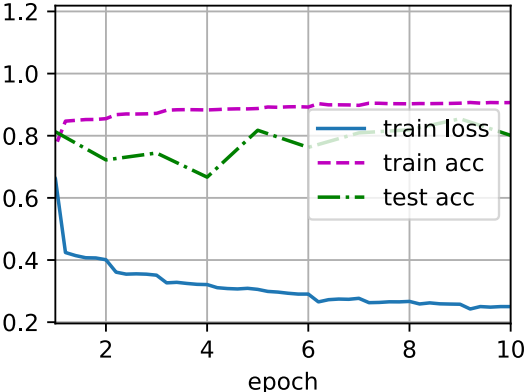
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.250, train acc 0.907, test acc 0.801
35560.7 examples/sec on cuda:0

让我们来看看从第一个批量归一化层中学到的拉伸参数gamma和便宜参数beta。

net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

(tensor([0.7562, 1.2784, 2.3527, 1.3189, 2.0457, 2.8424], device='cuda:0',
grad_fn=<ViewBackward>),
tensor([ 0.7436, -0.8156, -0.2711, -0.5087, 0.5847, -3.0033], device='cuda:0',
grad_fn=<ViewBackward>))

简明实现

除了使用我们刚刚定义的BatchNorm，我们也可以直接使用深度学习框架中定义的BatchNorm。该代码看起来几乎与我们上面的代码相同。

net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
nn.Linear(84, 10))

下面，我们使用相同超参数来训练模型。请注意，通常高级API变体运行速度快得多，因为它的代码已编译为C++或CUDA，而我们自定义代码由Python实现。

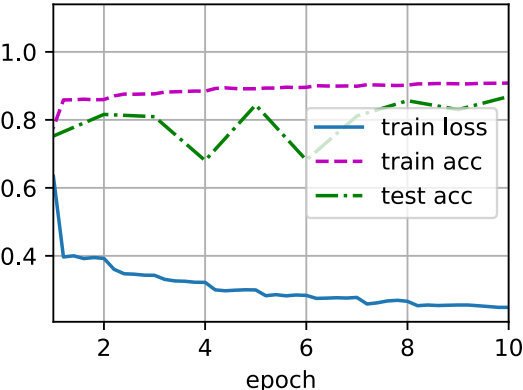
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.248, train acc 0.908, test acc 0.869
60219.9 examples/sec on cuda:0

争议

直观地说，批量归一化被认为可以使优化更加平滑。

然而，在提出批量归一化的论文中，作者除了介绍了其应用，还解释了其原理：通过减少内部协变量。然而这种解释更偏向于个人直觉。

但是批量归一化的效果很好，它适用于几乎所有图像分类器，并在学术界获得了数万引用。

以上就是Python深度学习理解pytorch神经网络批量归一化的详细内容，更多关于pytorch神经网络批量归一化的资料请关注我们其它相关文章！