java实现堆排序以及时间复杂度的分析
完全二叉树：从上到下，从左到右，每层的节点都是满的，最下边一层所有的节点都是连续集中在最左边。
二叉树的特点就是左子节点是父节点索引值的2倍加一，右子节点是父节点索引值的2倍加二
堆分为两种：大顶堆和小顶堆
大顶堆：在完全二叉树基础上，每个节点的值都大于或等于其左右子节点的值
小顶堆：在完全二叉树基础上，每个节点的值都大于或等于其左右子节点的值
堆排序就是根据先构建好的大顶堆或小顶堆进行排序的。
怎么构建大顶堆：
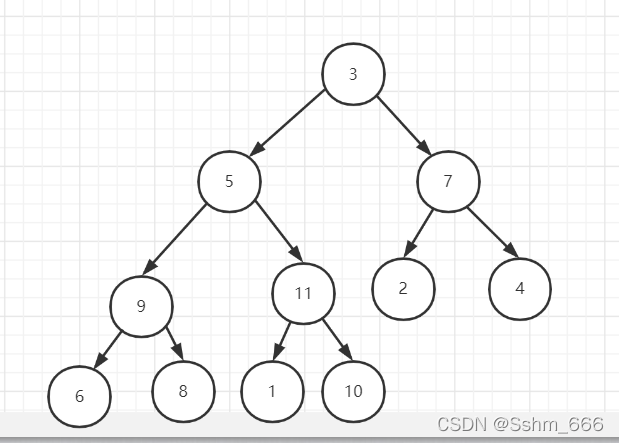
假如一个数组是：int[] arr= {3,5,7,9,1,2,4,6,8,11,10};它的完全二叉树形状如下图所示：
红色数字的是节点在数组中的索引值，它们之间的关系就是左子节点是父节点索引值的2倍加一，右子节点是父节点索引值的2倍加二
我们想把它构建成大顶堆就从二叉树最下面一层开始也就是从最后一个数组开始，先比较左右子树，找到最大的一个，用最大的和父节点进行比较如果子节点大就进行交换，交换结束后再比较此层左边的左右和父子节点进行交换。也就是从最下一层开始，从右到左开始比较，此层比较完进入上一层再从右到左开始比较以此循环。当到达上一层时会有一个问题就是如果换下来的父节点比子节点小我们还需要往下进行交换，我们就需要对它进行维护。
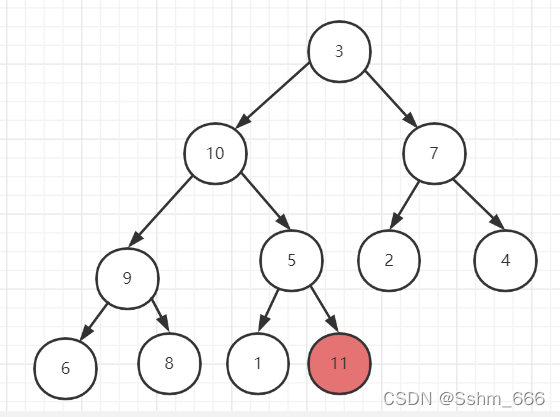
上面数组的例子按顺序构建的大顶堆如下图所示：
构建好的大顶堆的根节点总是最大的，我们根据这个特点进行排序。
我们把根节点和树的最后一个叶子节点进行交换即让数组的第一个数和最后一个数交换，交换后让最后一个数保持位置不再变化，我们再让其他节点再进行维护大顶堆，因为此时根节点是比子节点小的，重复以上操作直到需要根节点和他本身进行交换时排序完成
排序流程图如下：
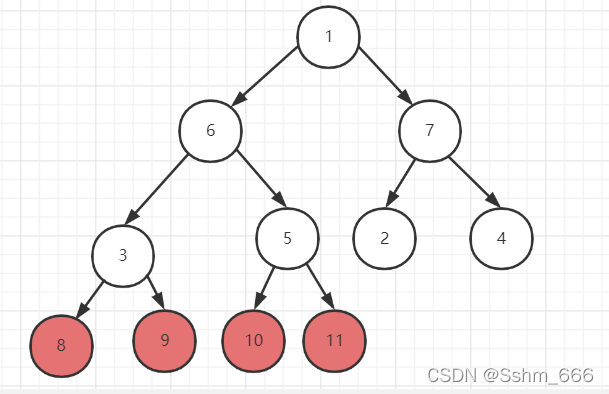
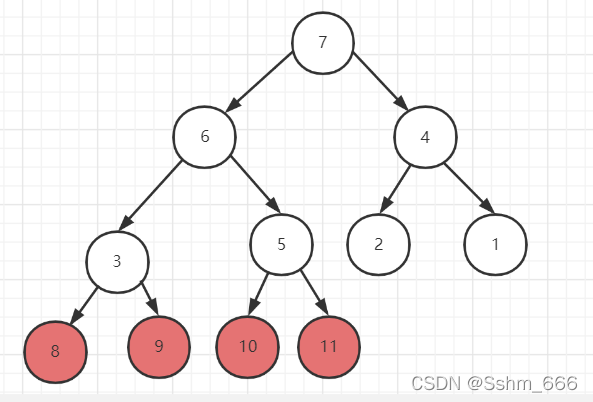
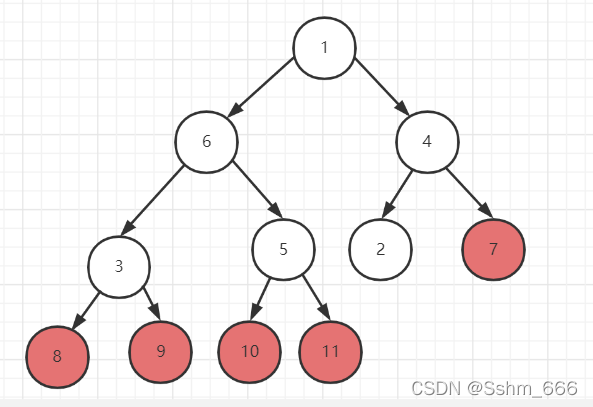
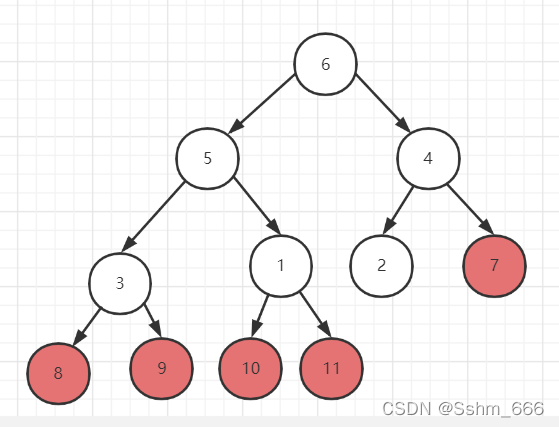
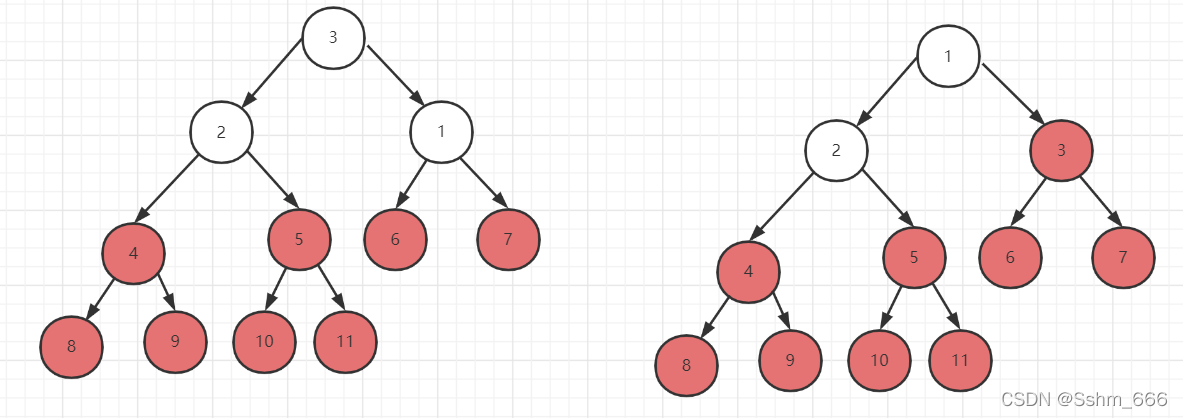
代码如下：
public class heapsort {
public static void main(String[] args) {
int[] arr= {3,5,7,9,1,2,4,6,8,11,10};
for(int p=arr.length-1;p>=0;p--) {
adjustheap(arr,p,arr.length);
}
heapsort(arr);
System.out.println(Arrays.toString(arr));
}
public static void heapsort(int[] arr) {
for(int i=arr.length-1;i>=0;i--) {
int temp=arr[i];
arr[i]=arr[0];
arr[0]=temp;
adjustheap(arr, 0, i);
}
}
public static void adjustheap(int[] arr, int p, int length) {
int temp=arr[p];
int left=p*2+1;
while(left<length) {
if(left+1<length&&arr[left]<arr[left+1]) {
left++;
}
if(temp>arr[left]) {
break;
}
arr[p]=arr[left];
p=left;
left=left*2+1;
}
arr[p]=temp;
}
输出结果如下：
时间复杂度：构建大顶堆的时间复杂度是O（nlogn）,n是main方法里的for循环，logn是构建大顶堆的方法的时间复杂度，排序的时间复杂度也是O（nlogn），所以堆排序的时间复杂度是O（nlogn）+O（nlogn）,也就是O（logn）
到此这篇关于java实现堆排序以及时间复杂度的分析的文章就介绍到这了,更多相关java 堆排序及时间复杂度内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！
相关推荐
-
JAVA堆排序算法的讲解
预备知识 堆排序 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序.首先简单了解下堆结构. 堆 堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆:或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆.如下图: 同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子 该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是: 大顶
-
深入解析堆排序的算法思想及Java代码的实现演示
一.基础知识 我们通常所说的堆是指二叉堆,二叉堆又称完全二叉树或者叫近似完全二叉树.二叉堆又分为最大堆和最小堆. 堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种.可以利用数组的特点快速定位指定索引的元素.数组可以根据索引直接获取元素,时间复杂度为O(1),也就是常量,因此对于取值效率极高. 最大堆的特性如下: 父结点的键值总是大于或者等于任何一个子节点的键值 每个结点的左子树和右子树都是一个最大堆 最小堆的特性如下: 父结点的键值总是小于或者等于任何一个
-
java堆排序原理与实现方法分析
本文实例讲述了java堆排序原理与实现方法.分享给大家供大家参考,具体如下: 堆是一个数组,被看成一个近似完全二叉树. 举例说明: 堆的性质: 1.已知元素在数组中的序号为i 其父节点的序号为 i/2的整数 其左孩子节点的序号为2*i 其右孩子节点的序号为2*i+1 2.堆分为最大堆和最小堆 在最大堆中,要保证父节点的值大于等于其孩子节点的值 在最小堆中,要保证父节点的值小于等于其孩子节点的值 java实现堆排序 public class MyHeapSort { public void Hea
-
Java 十大排序算法之堆排序刨析
二叉堆是完全二叉树或者是近似完全二叉树. 二叉堆满足二个特性︰ 1．父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值. 2．每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆). 任意节点的值都大于其子节点的值--大顶堆(最后输出从小到大排) 任意节点的值都小于其子节点的值---小顶堆(最后输出从大到小排) 堆排序步骤 1.堆化,反向调整使得每个子树都是大顶或者小顶堆(建堆) 2.按序输出元素∶把堆顶和最末元素对调,然后调整堆顶元素(排序) 堆排序代码实现(大顶堆) publ
-
java堆排序概念原理介绍
堆排序介绍: 堆排序可以分为两个阶段.在堆的构造阶段,我们将原始数组重新组织安排进一个堆中:然后在下沉排序阶段,我们从堆中按顺序取出所有元素并得到排序结果. 1.堆的构造,一个有效的方法是从右到左使用sink()下沉函数构造子堆.数组的每个位置都有一个子堆的根节点,sink()对于这些子堆也适用,如果一个节点的两个子节点都已经是堆了,那么在该节点上调用sink()方法可以把他们合并成一个堆.我们可以跳过大小为1的子堆,因为大小为1的不需要sink()也就是下沉操作,有关下沉和上浮操作可以参考我写
-
java 数据结构之堆排序（HeapSort）详解及实例
1 堆排序 堆是一种重要的数据结构,分为大根堆和小根堆,是完全二叉树, 底层如果用数组存储数据的话,假设某个元素为序号为i(Java数组从0开始,i为0到n-1),如果它有左子树,那么左子树的位置是2i+1,如果有右子树,右子树的位置是2i+2,如果有父节点,父节点的位置是(n-1)/2取整.最大堆的任意子树根节点不小于任意子结点,最小堆的根节点不大于任意子结点. 所谓堆排序就是利用堆这种数据结构的性质来对数组进行排序,在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的性质可知,最大的
-
java堆排序原理及算法实现
从堆排序的简介到堆排序的算法实现等如下: 1. 简介 堆排序是建立在堆这种数据结构基础上的选择排序,是原址排序,时间复杂度O(nlogn),堆排序并不是一种稳定的排序方式.堆排序中通常使用的堆为最大堆. 2. 堆的定义 堆是一种数据结构,是一颗特殊的完全二叉树,通常分为最大堆和最小堆.最大堆的定义为根结点最大,且根结点左右子树都是最大堆:同样,最小堆的定义为根结点最小,且根结点左右子树均为最小堆. 最大堆满足其每一个父结点均大于其左右子结点,最小堆则满足其每一个父结点均小于其左右子结点. 3.
-
Java实现堆排序（大根堆）的示例代码
堆排序是一种树形选择排序方法,它的特点是:在排序的过程中,将array[0,...,n-1]看成是一颗完全二叉树的顺序存储结构,利用完全二叉树中双亲节点和孩子结点之间的内在关系,在当前无序区中选择关键字最大(最小)的元素. 1. 若array[0,...,n-1]表示一颗完全二叉树的顺序存储模式,则双亲节点指针和孩子结点指针之间的内在关系如下: 任意一节点指针 i:父节点:i==0 ? null : (i-1)/2 左孩子:2*i + 1 右孩子:2*i + 2 2. 堆的定义:n个关键字序列a
-
java实现堆排序以及时间复杂度的分析
完全二叉树:从上到下,从左到右,每层的节点都是满的,最下边一层所有的节点都是连续集中在最左边. 二叉树的特点就是左子节点是父节点索引值的2倍加一,右子节点是父节点索引值的2倍加二 堆分为两种:大顶堆和小顶堆 大顶堆:在完全二叉树基础上,每个节点的值都大于或等于其左右子节点的值 小顶堆:在完全二叉树基础上,每个节点的值都大于或等于其左右子节点的值 堆排序就是根据先构建好的大顶堆或小顶堆进行排序的. 怎么构建大顶堆: 假如一个数组是:int[] arr
-
Java详细讲解堆排序与时间复杂度的概念
目录 一.堆排序 1.什么是堆排序 2.堆排序思想 3.代码实现 二.时间复杂度分析 1.初始化建堆 2.排序重建堆 3.总结 一.堆排序 1.什么是堆排序 (1)堆排序:堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法.堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点. (2)堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆:或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
-
Java编程中ArrayList源码分析
之前看过一句话,说的特别好.有人问阅读源码有什么用?学习别人实现某个功能的设计思路,提高自己的编程水平. 是的,大家都实现一个功能,不同的人有不同的设计思路,有的人用一万行代码,有的人用五千行.有的人代码运行需要的几十秒,有的人只需要的几秒..下面进入正题了. 本文的主要内容: · 详细注释了ArrayList的实现,基于JDK 1.8 . ·迭代器SubList部分未详细解释,会放到其他源码解读里面.此处重点关注ArrayList本身实现. ·没有采用标准的注释,并适当调整了代码的缩进以方便介
-
java finally块执行时机全面分析
java里 finally 关键字通常与try catch块一起使用.用来在方法结束前或发生异常时做一些资源释放的操作.最近也看到网上有一些讨论try catch finally关键词执行的顺序的文章,并给出了finally块是在方法最后执行的. 这些观点普遍认为: 1) finally关键词是在程序return语句后返回上一级方法前执行的,其中返回值会保存在一个临时区域,待执行完finally块的部分后,在将临时区域的值返回. 2) 若finally块里有返回值会替换掉程序中前面的try 或c
-
java 中Buffer源码的分析
java 中Buffer源码的分析 Buffer Buffer的类图如下: 除了Boolean,其他基本数据类型都有对应的Buffer,但是只有ByteBuffer才能和Channel交互.只有ByteBuffer才能产生Direct的buffer,其他数据类型的Buffer只能产生Heap类型的Buffer.ByteBuffer可以产生其他数据类型的视图Buffer,如果ByteBuffer本身是Direct的,则产生的各视图Buffer也是Direct的. Direct和Heap类型Buff
-
java 中volatile和lock原理分析
java 中volatile和lock原理分析 volatile和lock是Java中用于线程协同同步的两种机制. Volatile volatile是Java中的一个关键字,它的作用有 保证变量的可见性 防止重排序 保证64位变量(long,double)的原子性读写 volatile在Java语言规范中规定的是 The Java programming language allows threads to access shared variables (§17.1). As a rule,
-
一种c#深拷贝方式完胜java深拷贝(实现上的对比分析)
楼主是一名asp.net攻城狮,最近经常跑java组客串帮忙开发,所以最近对java的一些基础知识特别上心.却遇到需要将一个对象深拷贝出来做其他事情,而原对象保持原有状态的情况.(实在是不想自己new一个出来,然后对着一堆字段赋值......好吧,再此之前我没有关心是否项目框架有深拷贝的方法),然后就想着用反射实现吧....接下来 是我自己的原因,还是真的不存在这样的纯用反射实现的深拷贝方式....(c#是有纯反射实现的) 但也不能算自己白忙活吧,也找到了其他实现深拷贝的方式(但是每种方式我都觉
-
JAVA 枚举单例模式及源码分析的实例详解
JAVA 枚举单例模式及源码分析的实例详解 单例模式的实现有很多种,网上也分析了如今实现单利模式最好用枚举,好处不外乎三点: 1.线程安全 2.不会因为序列化而产生新实例 3.防止反射攻击但是貌似没有一篇文章解释ENUM单例如何实现了上述三点,请高手解释一下这三点: 关于第一点线程安全,从反编译后的类源码中可以看出也是通过类加载机制保证的,应该是这样吧(解决) 关于第二点序列化问题,有一篇文章说枚举类自己实现了readResolve()方法,所以抗序列化,这个方法是当前类自己实现的(解决) 关于
-
基于java线程安全问题及原理性分析
1.什么是线程安全问题? 从某个线程开始访问到访问结束的整个过程,如果有一个访问对象被其他线程修改,那么对于当前线程而言就发生了线程安全问题:如果在整个访问过程中,无一对象被其他线程修改,就是线程安全的. 2.线程安全问题产生的根本原因 首先是多线程环境,即同时存在有多个操作者,单线程环境不存在线程安全问题.在单线程环境下,任何操作包括修改操作都是操作者自己发出的,操作者发出操作时不仅有明确的目的,而且意识到操作的影响. 多个操作者(线程)必须操作同一个对象,只有多个操作者同时操作一个对象,行为