Python可视化神器pyecharts绘制仪表盘

目录
  • 仪表盘
  • 仪表盘模板系列
    • 假期剩余额度
    • 任务完成率
    • 多色仪表盘
    • 仪表盘内部字体添加

仪表盘

仪表盘的效果我只能说炫酷而已，如果想要运用在实际的场景中，我其实也不清楚那个场景比较适合，但是pyecharts毕竟是炫酷可视化的利器，炫酷自然也就有它了。

小汽车仪表盘是长这样的，下面我们来看看pyecharts的仪表盘是怎么样子的。

仪表盘模板系列

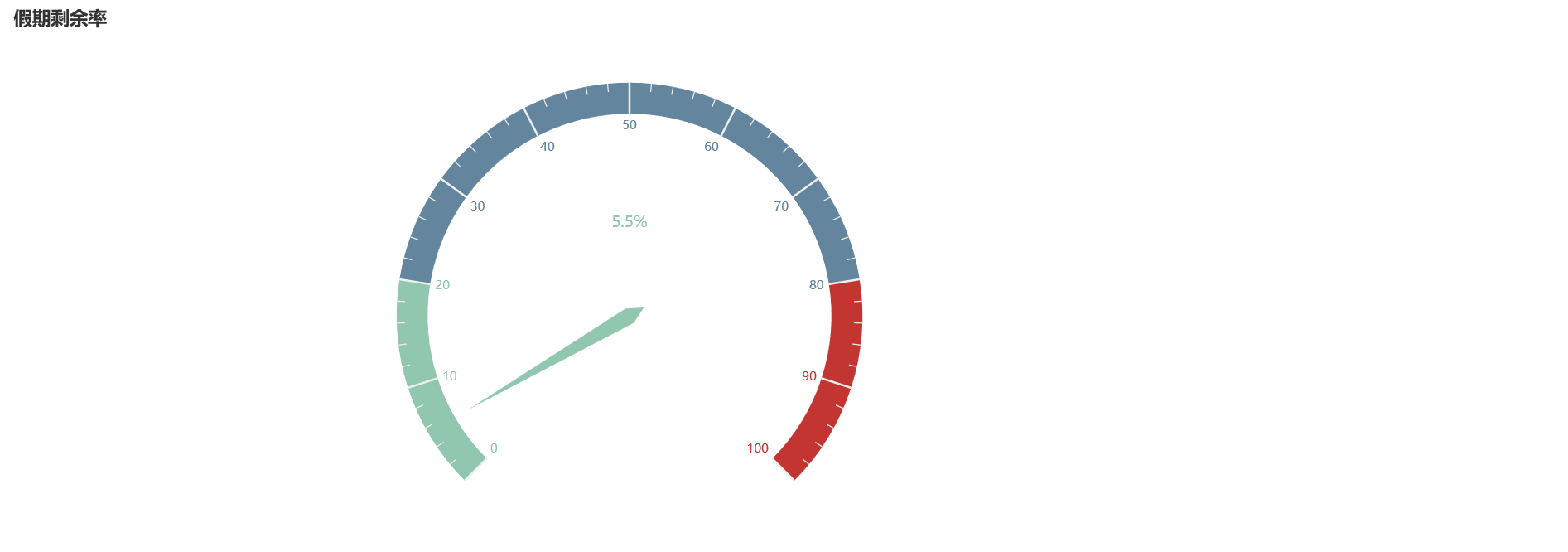
假期剩余额度

import pyecharts.options as opts
from pyecharts.charts import Gauge
(
Gauge(init_opts=opts.InitOpts(width="1200px", height="600px"))
.add(series_name="", data_pair=[["", 5.5]])
.set_global_opts(
title_opts=opts.TitleOpts(title="假期剩余率"),
legend_opts=opts.LegendOpts(is_show=False),
tooltip_opts=opts.TooltipOpts(is_show=True, formatter="{a} <br/>{b} : {c}%"),
)
.render("完成率.html")
)

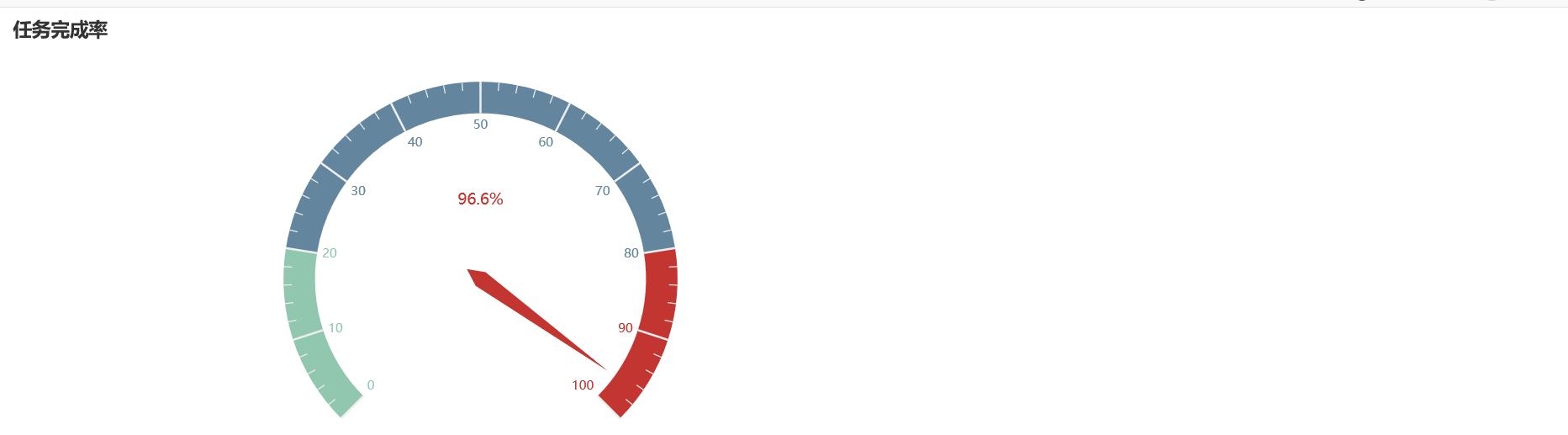
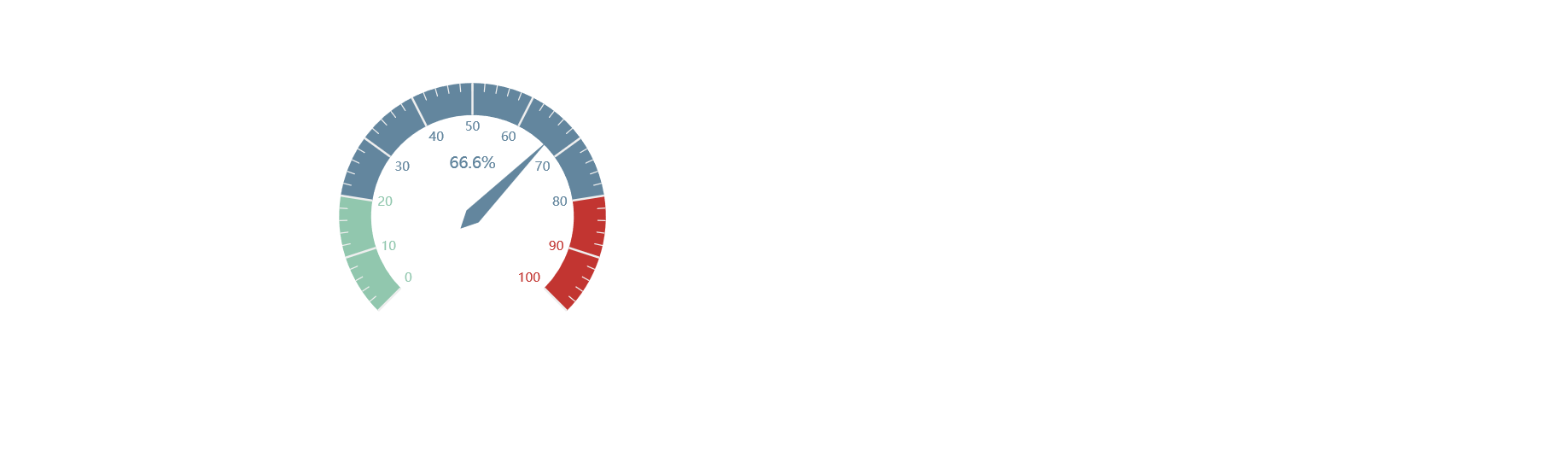
任务完成率

from pyecharts import options as opts
from pyecharts.charts import Gauge
c = (
Gauge()
.add("", [("", 96.6)]
)
.set_global_opts(title_opts=opts.TitleOpts(title="任务完成率"))
.render("任务完成率.html")
)

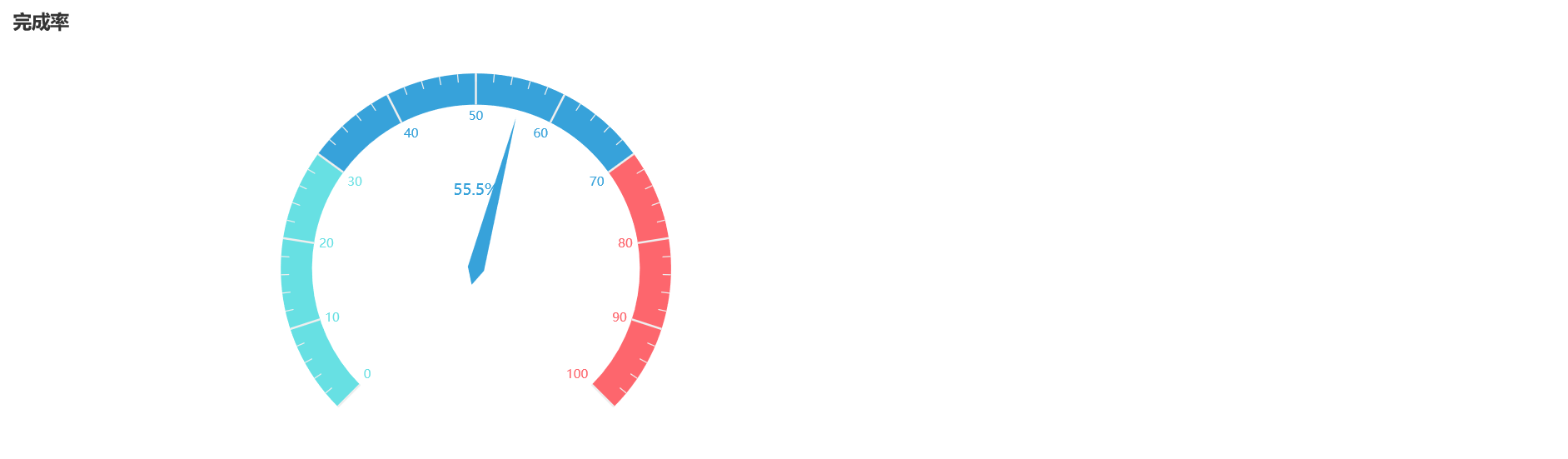
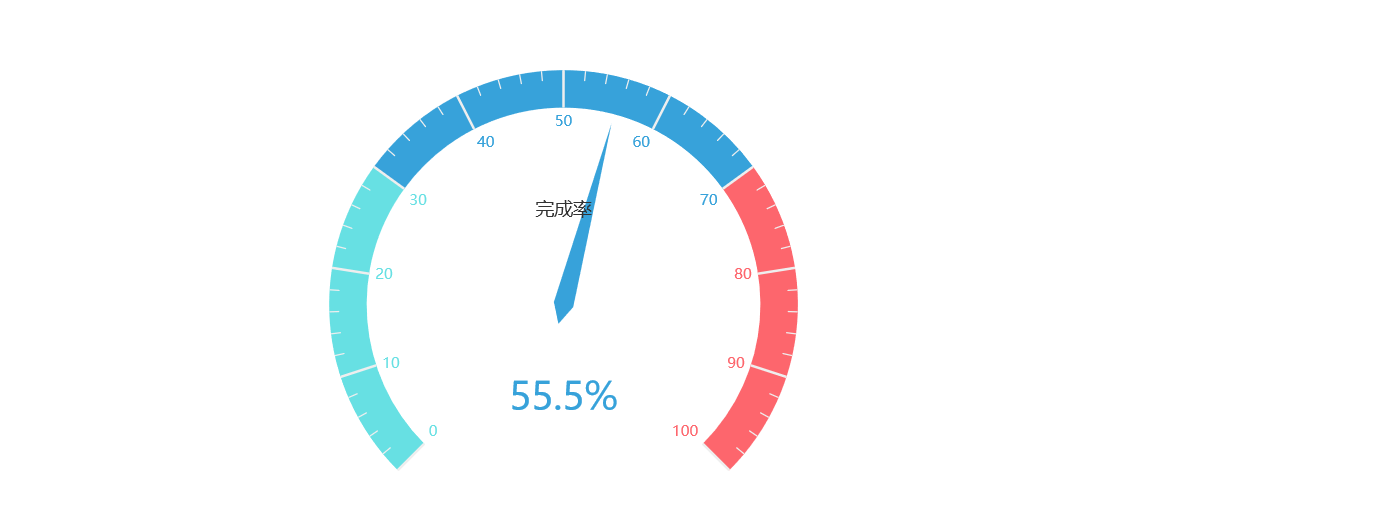
多色仪表盘

from pyecharts import options as opts
from pyecharts.charts import Gauge

c = (
Gauge()
.add(
"",
[("", 55.5)],
axisline_opts=opts.AxisLineOpts(
linestyle_opts=opts.LineStyleOpts(
color=[(0.3, "#67e0e3"), (0.7, "#37a2da"), (1, "#fd666d")], width=30
)
),
)
.set_global_opts(
title_opts=opts.TitleOpts(title="完成率"),
legend_opts=opts.LegendOpts(is_show=False),
)
.render("多色仪表盘.html")
)

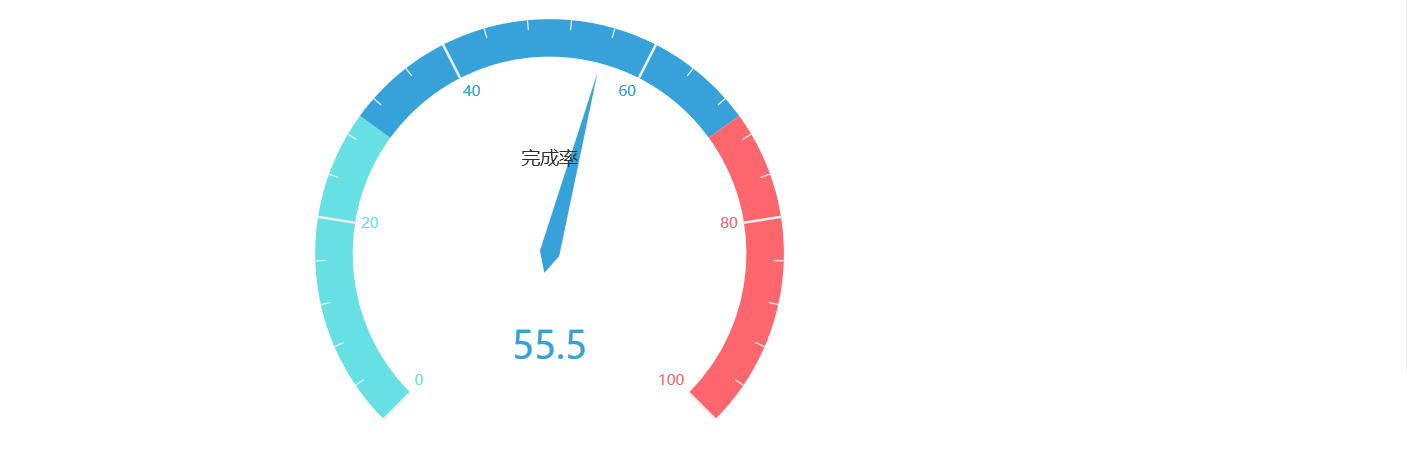
仪表盘内部字体添加

到此这篇关于Python可视化神器pyecharts绘制仪表盘的文章就介绍到这了,更多相关python绘制仪表盘内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Python可视化神器pyecharts绘制地理图表

    Python可视化神器pyecharts绘制地理图表

    目录 地理图表 地理图表之热力图系列模板 人口流动趋势图(中国) 中国城市分段热力图 重庆省份微塑料分布热力图 中国城市连续热力图 中国城市热力动态图 中国城市散点热力图 地理图表 什么是地理图表?地理图表有什么作用?地理图表主要应用在那些领域? 其实这些问题看看下面的实例图形就已不攻自破了,地理图表一看首先就是地图,然后在地理图表里面展示数据,比如说热力图,趋势流动图,人口密集分布图,反正地理坐标相关的就可以运用在这个里面,其次图形支持全球地图,全球国家,中国,中国的所有的省份的地图,反正应有

  • Python绘制散点图之可视化神器pyecharts

    Python绘制散点图之可视化神器pyecharts

    目录 散点图 什么是散点图? 散点图有什么用处? 散点图的基本构成要素 散点图模板系列 简单散点图 多维数据散点图 散点图显示分割线 散点图凸出大小(二维) 3D散点图展示 动态涟漪散点图 箭头标志散点图 散点图 什么是散点图? 散点图是指在数理统计回归分析中,数据点在直角坐标系平面上的分布图, 散点图​​表示因变量随自变量而变化的大致趋势,由此趋势可以选择合适的函数进行经验分布的拟合,进而找到变量之间的函数关系. 散点图有什么用处? 1.数据用图表来展示,显然比较直观,在工作汇报等场合能起到事

  • Python可视化神器pyecharts绘制漏斗图

    Python可视化神器pyecharts绘制漏斗图

    目录 漏斗图 漏斗图系列模板 尖顶型漏斗图 锥子型漏斗 三角形漏斗 连接型漏斗 漏斗图 漏斗图是由Light等在1984年提出,一般以单个研究的效应量为横坐标,样本含量为纵坐标做的散点图.效应量可以为RR.OR和死亡比或者其对数值等.理论上讲,被纳入Meta分析的各独立研究效应的点估计,在平面坐标系中的集合应为一个倒置的漏斗形,因此称为漏斗图. 样本量小,研究精度低,分布在漏斗图的底部,向周围分散: 样本量大,研究精度高,分布在漏斗图的顶部,向中间集中. 漏斗图法的优点是: 简单易行,只需要被纳

  • 以大热剧《觉醒年代》为例用Python绘制可视化仪表盘

    以大热剧《觉醒年代》为例用Python绘制可视化仪表盘

    前言 <觉醒年代>被称为是继<走向共和>后的又一部历史神剧.自开播以来,豆瓣上的评分也是从最初的8.3分飙升到9.2分,并且在最近的上海电视节白玉兰奖中获得多项提名. 数据的可视化 Pyecharts中的页面组件Page能够很好地将许多绘制出来的页面组合到一个页面当中去,首先我们先导入需要用到的模块, import pandas as pd from pyecharts.charts import Bar, Page from pyecharts import options as

  • Python可视化神器pyecharts之绘制箱形图

    Python可视化神器pyecharts之绘制箱形图

    目录 箱形图 概念 用处 箱形图系列模板 第一个箱形图 复杂一点的图例 箱形图 概念 后面的图形都是一些专业的统计图形,当然也会是我们可视化的对象. 箱形图(Box-plot)又称为盒须图.盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图.因形状如箱子而得名.在各种领域也经常被使用,常见于​​品质管理​​.它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比 较.箱线图的绘制方法是:先找出一组数据的上边缘.下边缘.中位数和两个四分位数:然后, 连接两个四分位数画出箱体:再将

  • Python可视化神器pyecharts之绘制地理图表练习

    Python可视化神器pyecharts之绘制地理图表练习

    目录 炫酷地图 3D炫酷地图模板系列 重庆市3D地图展示 中国3D地图 中国3D数据地图(适合做数据可视化) 全国行政区地图(带城市名字) 地球展示 炫酷地图 前期我们介绍了很多的地图模板,不管是全球的还是中国的,其实我感觉都十分的炫酷,哈哈哈,可是还有更加神奇的,更加炫酷的地图模板,下面让我们一起一饱眼福吧! 3D炫酷地图模板系列 重庆市3D地图展示 from pyecharts import options as opts from pyecharts.charts import Map3D

  • Python可视化神器pyecharts绘制雷达图

    Python可视化神器pyecharts绘制雷达图

    目录 雷达图 雷达图模板系列 基础雷达图 单例雷达图 空气质量模板 颜色雷达图 雷达图 雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法.轴的相对位置和角度通常是无信息的. 雷达图也称为网络图,蜘蛛图,星图,蜘蛛网图,不规则多边形,极坐标图或Kiviat图.它相当于​ ​平行坐标图​​,轴径向排列. 平行坐标图: 平行坐标图是一种通常的可视化方法, 用于对 高维几何 和 多元数据 的可视化. 为了表示在高维空间的一个点集,在N条平行的线的背景下,(一

  • Python可视化神器pyecharts绘制水球图

    Python可视化神器pyecharts绘制水球图

    目录 水球图 双水球图显示 正方形水球图 圆球水球图 数据精度水球图 炫酷水球超级好看 水球图 水球图首先是动态的效果,像水流一样波动,所以看起来比较的舒服,一般用于业务里面的完成率,其实和之前的仪表盘有点类似,但是我个人绝对水球图更加的好,因为看起来比较的炫酷. from pyecharts import options as opts from pyecharts.charts import Liquid from pyecharts.globals import SymbolType c

  • Python可视化神器pyecharts绘制柱状图

    Python可视化神器pyecharts绘制柱状图

    目录 主题介绍 图表参数 主题详解 柱状图模板系列 海量数据柱状图动画展示 收入支出柱状图(适用于记账) 三维数据叠加 柱状图与折线图多维展示(同屏展示) 单列多维数据展示 3D柱状图 主题介绍 pyecharts里面有很多的主题可以供我们选择,我们可以根据自己的需要完成主题的配置,这样就告别了软件的限制,可以随意的发挥自己的艺术细胞了. 图表参数 ''' def add_yaxis( # 系列名称,用于 tooltip 的显示,legend 的图例筛选. series_name: str, #

  • Python可视化神器pyecharts绘制桑基图

    Python可视化神器pyecharts绘制桑基图

    目录 桑基图 桑基图系列模板 第一个桑基图 复杂桑基图 桑基图 桑基图(Sankey diagram),即桑基能量分流图,也叫桑基能量平衡图.它是一种特定类型的流程图,图中延伸的分支的宽度对应数据流量的大小,通常应用于​​能源​​​.材料成分.​​金融​​​等数据的可视化分析.因1898年Matthew Henry Phineas Riall Sankey绘制的“​​蒸汽机​​的能源效率图”而闻名,此后便以其名字命名为“桑基图”. 桑基图最明显的特征就是,始末端的分支宽度总和相等,即所有主支宽度

随机推荐