Python光学仿真学习处理高斯光束分布图像

目录
  • 通过python处理光斑图像
    • 1 相关包与图像读取
    • 2 图像截取
    • 3显示强度
    • 4数据拟合
  • 问题

通过python处理光斑图像

1 相关包与图像读取

首先需要科学计算必备包numpy和画图包matplotlib.pyplot，我们通过后者进行图像数据的读取.

plt.imread读取图片之后为数据格式为numpy数组，可以通过成员函数astype将整型数据变成浮点型，有利于后期处理。

plt.imshow将img的数据加载到窗口，plt.show()显示绘图窗口，默认显示为伪彩图。

python自动画出了伪彩图，可以通过在plt.imshow的过程中输入cmap参数使之得到灰度图

>>> plt.imshow(img,cmap=plt.cm.gray)
<matplotlib.image.AxesImage object at 0x000002E84F5B4788>
>>> plt.show()

2 图像截取

由于光斑只占据图片中很小一部分，大量的冗余信息等同于噪声，会对后期的数据处理造成影响，故需截取感兴趣的区域，plt.ginput函数提供一种交互操作方法，可返回鼠标点击的位置，其输入参数为选取点数，输出为点击的点的坐标。

>>> plt.imshow(img)
<matplotlib.image.AxesImage object at 0x000002E857A21448>
>>> plt.ginput(2)
[(717.0757575757577, 299.8290043290042), (783.5692640692644, 233.33549783549768)]

在python中，通过方括号进行矩阵索引，图片的截取方法为

>>> roi = img[233:299,717:783]
>>> plt.imshow(roi)
<matplotlib.image.AxesImage object at 0x000002E84F5B4948>
>>> plt.show()

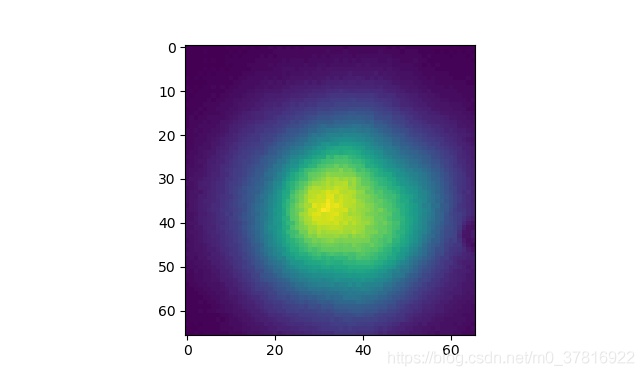
3显示强度

为了更加直观地反映光斑强度，以图片行列为坐标，可以绘制3d强度图。

绘制二维曲线，要求输入相应的自变量和因变量，通过点和点的一一对应，画出曲线。三维图像绘制亦然，通过np.meshgrid生成网格坐标，作为其 x , y x,y x,y向的自变量，其输入参数为两个一维数组，返回两个二维数组，用以表示这两个数组方向的坐标。

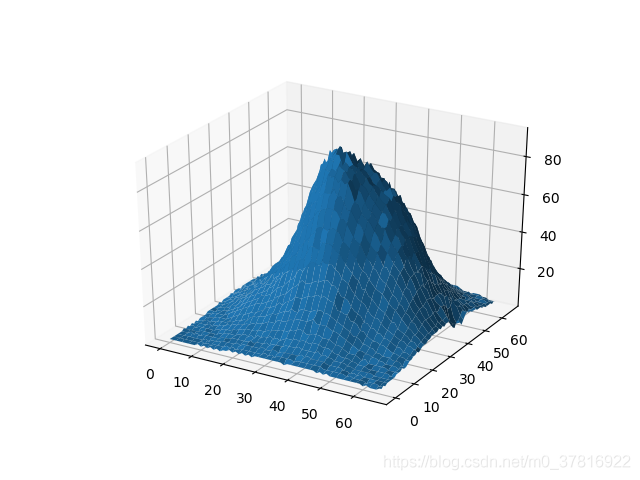
>>> xNum,yNum = roi.shape						#获取roi的维度
>>> xAxis,yAxis = np.meshgrid(range(yNum),range(xNum))	#range创建长度为xNum的自然数列
>>> ax = plt.gca(projection='3d')				#建立3D坐标轴
>>> ax.plot_surface(xAxis,yAxis,roi)			#创建面元图
<mpl_toolkits.mplot3d.art3d.Poly3DCollection object at 0x0000019EAFF19D48>
>>> plt.show()

结果为

4数据拟合

光斑在空间中的分布形式呈中心对称的特征，故可抽取出其径向坐标进行降维操作，考虑到数据的稳定性，并排除非信号区的影响，可提取每一列的最大值

>>> arr = np.max(roi,0)
>>> x = np.arange(len(arr))
>>> plt.plot(x,arr)
[<matplotlib.lines.Line2D object at 0x0000019EB469EB48>]
>>> plt.show()

结果如图所示

在python中，需要通过引入科学计算库scipy中的优化拟合包optimize中的curve_fit函数来进行数据的高斯拟合。curve_fit的输入参数为拟合函数，自变量和因变量；输出参数为拟合函数中的其他参数以及拟合评价参数。

其中高斯函数的表达形式为

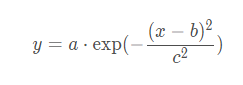
>>> from scipy.optimize import curve_fit
>>> def gauss(x, a, b, c):
...     return a*np.exp(-(x-b)**2/c**2)
...
>>> abc,  para = curve_fit(gauss,x,arr)
>>> abc							#即上式中的a,b,c
array([89.72326971, 35.58522403, 20.86186403])
>>> fitValue = gauss(x,abc[0],abc[1],abc[2])	#拟合值
>>> plt.scatter(x,arr)			#绘制原始数据的散点图
<matplotlib.collections.PathCollection object at 0x0000019EB5438D88>
>>> plt.plot(x,fitValue)		#绘制拟合数据的曲线图
[<matplotlib.lines.Line2D object at 0x0000019EB46D4048>]
>>> plt.show()

问题

如果包没有安装的话，可以在命令行中用pip文件进行安装

> pip install numpy
> pip install matplotlib
> pip install scipy

以上就是Python光学仿真学习处理高斯光束分布图像的详细内容，更多关于Python处理高斯光束分布图像的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • Python光学仿真教程实现光线追踪

    Python光学仿真教程实现光线追踪

    目录 光线追迹 几何抽象 光线 线段与圆弧 光线追迹 得益于计算机的计算的能力,通过追踪具有代表性的光线的传播轨迹,可以更加精确地描述光学系统的性能,光线追迹方法也因此大展其能,诸如Zemax.tracepro等软件便都提供了相应的功能. 而建立在折射定律基础之上的光线追迹方法,对数学功底要求较低,所以比较适合作为python初学者的入门项目.在接下来的这一章,希望通过对光线追迹的实现,掌握python中的列表.元组.字典.集合等数据类型的基本概念,并且对面向对象与函数式编程有一个基本的了解.

  • python光学仿真实现光线追迹之空间关系

    python光学仿真实现光线追迹之空间关系

    目录 空间关系 相交判定 射线排序 线弧关系 点弧关系 空间关系 变化始于相遇,所以交点是一切的核心. 相交判定 首先考察一束光线能否打在某个平面镜上.光线被抽象成了一个列表[a,b,c],平面镜则被抽象成为由两个点构成的线段[(x1,y1),(x2,y2)].两条直线的交点问题属于初等数学范畴,需要先将线段转换成直线的形式,然后再求交点.但是两条直线的交点可能落在线段的外面,从而不具有判定的意义. 如果我们的光学系统中有大量的光学元件,那么如果有一种方法可以快速判断光线是否与光学元件有交点,将

  • python光学仿真实现光线追迹折射与反射的实现

    python光学仿真实现光线追迹折射与反射的实现

    目录 折射与反射 平面反射 平面折射 python实现 弧面问题 折射与反射 光线与光学元件相互作用,无非只有两件事,反射和透射.而就目前看来,我们所常用的光学元件,也无非有两种表面,即平面和球面,二维化之后就简化成了射线与线段,射线与劣弧的关系. 平面反射 无论从哪个角度来看,平面的反射折射都要比球面更简单,而反射问题要比折射问题更简单,所以,我们首先处理平面的反射问题. 反射定律即入射角等于反射角,心念及此,最为循规蹈矩的思路必然是先找到入射光线和平面的夹角,然后用这个夹角和平面(在二维空间

  • python光学仿真面向对象光学元件类的实现

    光学元件类 平面反射镜是一种极为简单的模型,因为我们只需要考虑一个平面即可.但是除此之外的其他光学元件,可能会变得有些复杂:我们必须考虑光在入射面和出射面的行为. 这当然是一句废话,而且我们也有了一个初步的解决方案:将光学元件拆成前表面和后表面即可.如果光需要在光学元件中反射多次,那就将光学元件拆成需要反射次数的表面个数即可,完美而无脑. 这说明我们已经熟悉了程序员的思维,我们眼中的世界已经不再是一个所见即所得的世界,我们看到的是一个个抽象零部件的表现.但是也不要惊慌,程序员和正常人也未必有很大

  • Python光学仿真光的偏振编程理解学习

    Python光学仿真光的偏振编程理解学习

    目录 光的偏振 光的偏振 由于光波是横波,所以对于任意一个光波,其振幅方向与传播方向在一个固定的平面内.换言之,一束光波可以存在振幅方向不同的一群光波,对于其中一个光波而言,其振幅方向即为偏振方向. 可以画出其示意图 #偏振光演示 import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D as axd def polarShow(): z = np.arange(0,5,0

  • Python实现病毒仿真器的方法示例(附demo)

    最近新冠在神州大陆横行,全国上下一心抗击疫情.作为一枚程序员,我也希望可以为抗击疫情做出自己的贡献,钟院士一直劝说大家不要出门,减少人口间的流动.对此,我特意做了一个病毒仿真器,探询冠状病毒传播. 1. 仿真效果 仿真开始,一开始只有5个发病者,传播率为0.8,潜伏期为14天 由于人口的流动,以及医院床位的隔离,一开始病毒扩撒不是很速度 随着医院床位满了,隔离失败,加上人口的流动,病患数开始几何式的增加 2. 什么是仿真器 仿真器(emulator)以某一系统复现另一系统的功能.与计算机模拟系统

  • Python光学仿真学习处理高斯光束分布图像

    Python光学仿真学习处理高斯光束分布图像

    目录 通过python处理光斑图像 1 相关包与图像读取 2 图像截取 3显示强度 4数据拟合 问题 通过python处理光斑图像 1 相关包与图像读取 首先需要科学计算必备包numpy和画图包matplotlib.pyplot,我们通过后者进行图像数据的读取. plt.imread读取图片之后为数据格式为numpy数组,可以通过成员函数astype将整型数据变成浮点型,有利于后期处理. plt.imshow将img的数据加载到窗口,plt.show()显示绘图窗口,默认显示为伪彩图. pyth

  • Python光学仿真学习Gauss高斯光束在空间中的分布

    Python光学仿真学习Gauss高斯光束在空间中的分布

    目录 Gauss光束强度的表达式为 如图所示 左上图和左下图表示激光传输过程中的其束腰半径的变化情况:右图则表示高斯光束某一横截面处激光的能量分布. 绘制代码如下 import matplotlib.pyplot as plt import numpy as np def setLabel(ax,*args): ax.set_xlabel(args[0]) ax.set_ylabel(args[1]) if len(args)==3: ax.set_zlabel(args[2]) def dra

  • python光学仿真学习wxpython创建手速测试程序

    python光学仿真学习wxpython创建手速测试程序

    滚动条是什么大家自然都是知道的,可以非常直观地显示数据的变化,或者可以非常方便地改变某些数值. 此前在介绍按钮.静态文本.输入文本这三个控件时,相对来说比较乏味,所以这次我们采用需求引导的模式.假如想编写一个软件用来检测打字速度,同时能够非常直观地通过滚动条来显示出来,应该怎么写? 我们大致需要三个控件,文本输入控件用来输入文字:静态文本控件用于显示速度:滚动条用来动态地显示速度.同时,还需要知道系统的时间,总之,代码如下 import wx import time #时间模块 class te

  • Python光学仿真学习衍射算法初步理解

    Python光学仿真学习衍射算法初步理解

    对衍射最经典的解释是Huygens-Fresnel原理,Huygens认为波阵面上每一点都会成为新的波源,这些子波源的相互干涉就形成了衍射.这显然是一种离散的观点,仿佛是专门为程序员准备的一样. 假设一束光打在一个方形孔上,这个方形孔被细分成 n×n个网格,那么每个网格都相当于是一个小孔,而这些小孔的互相干涉,即为衍射.随着网格不断被细分,最终可以逼近真实的衍射情形.那么,假设矩孔处为等相位面,其网格坐标为  (i,j),到衍射屏距离为 d d d,那么对于衍射屏上任意一点P(x,y),其光强为

  • Python光学仿真理解Jones矩阵学习

    Python光学仿真理解Jones矩阵学习

    目录 Jones向量 Jones矩阵 Jones矩阵的表示 Jones向量 假设光波沿z轴传播,那么其三个方向的电场分量可以表示为 Jones矩阵 能够保证二维列向量形状不变的运算有无穷多种,但最符合我们直觉的一定是 2 × 2矩阵.好在这种矩阵已经可以提供足够多的运算,从而满足我们描述偏振变化的需求. 光在通过波片之后,会在不同方向产生差异性的相位延迟,对于与x轴角度为 Ψ,相位差为 Φ 的波片,其Jones矩阵为 Jones矩阵的表示 为了对Jones矩阵所对应的偏振状态进行绘制,我们需要进

  • Python光学仿真之对光的干涉理解学习

    Python光学仿真之对光的干涉理解学习

    光的干涉 干涉即两束光在叠加过程中出现的强度周期性变化情况,其最简单的案例即为杨氏双缝干涉. 如图所示,光从 S S S点发出,通过两个狭缝 S 1 , S 2 S_1,S_2 S1​,S2​,最终汇聚在右侧的干涉屏上,在不同位置处将会产生不同的相位差. import numpy as np import matplotlib.pyplot as plt #两束光叠加 waveAdd = lambda I1,I2,theta : I1+I2+2*np.sqrt(I1*I2)*np.cos(the

  • python光学仿真相速度和群速度计算理解学习

    python光学仿真相速度和群速度计算理解学习

    目录 波动模型 相速度 群速度 从编程的角度来说,波动光学在某些情况下可以简单地理解为在光线模型的基础上,引入一个相位项. 波动模型 一般来说,三个特征可以确定空间中的波场:频率.振幅和相位,故光波场可表示为: import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D z = np.arange(15,200)*10 #单位为nm x = np.arange(15,200)

  • Python光学仿真从Maxwell方程组到波动方程矢量算法理解学习

    Python光学仿真从Maxwell方程组到波动方程矢量算法理解学习

    Maxwell方程组是十九世纪最伟大的公式,代表了传统物理学人对公式美学的孜孜追求,也影响了无数后来者的物理美学品味. 回顾历史,当1864年,Maxwell发出那篇著名的<电磁场的动力学理论>时,实则列出了二十个公式,以总结前人的物理学成果,我们将分量公式合并为矢量,可以得到八个式子,即 以上符号分别表示 二十年后,Heaviside对这二十个公式进行重新编排,得到了我们熟悉的形式,并将其命名为麦克斯韦方程组: 对上式中左侧两个旋度公式再取旋度,得到 其中, ∇ E = 0,所以可得到波动方

  • python光学仿真通过菲涅耳公式实现波动模型

    python光学仿真通过菲涅耳公式实现波动模型

    从物理学的机制出发,波动模型相对于光线模型,显然更加接近光的本质:但是从物理学的发展来说,波动光学旨在解决几何光学无法解决的问题,可谓光线模型的一种升级.从编程的角度来说,波动光学在某些情况下可以简单地理解为在光线模型的基础上,引入一个相位项. 波动模型 一般来说,三个特征可以确定空间中的波场:频率.振幅和相位,故光波场可表示为: import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import

随机推荐