Python深度学习之使用Pytorch搭建ShuffleNetv2

一、model.py

1.1 Channel Shuffle

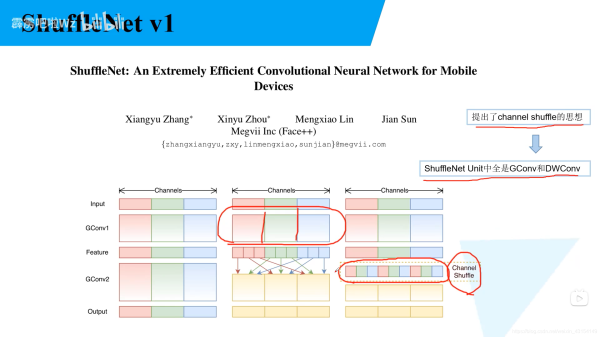
def channel_shuffle(x: Tensor, groups: int) -> Tensor:

    batch_size, num_channels, height, width = x.size()
    channels_per_group = num_channels // groups

    # reshape
    # [batch_size, num_channels, height, width] -> [batch_size, groups, channels_per_group, height, width]
    x = x.view(batch_size, groups, channels_per_group, height, width)

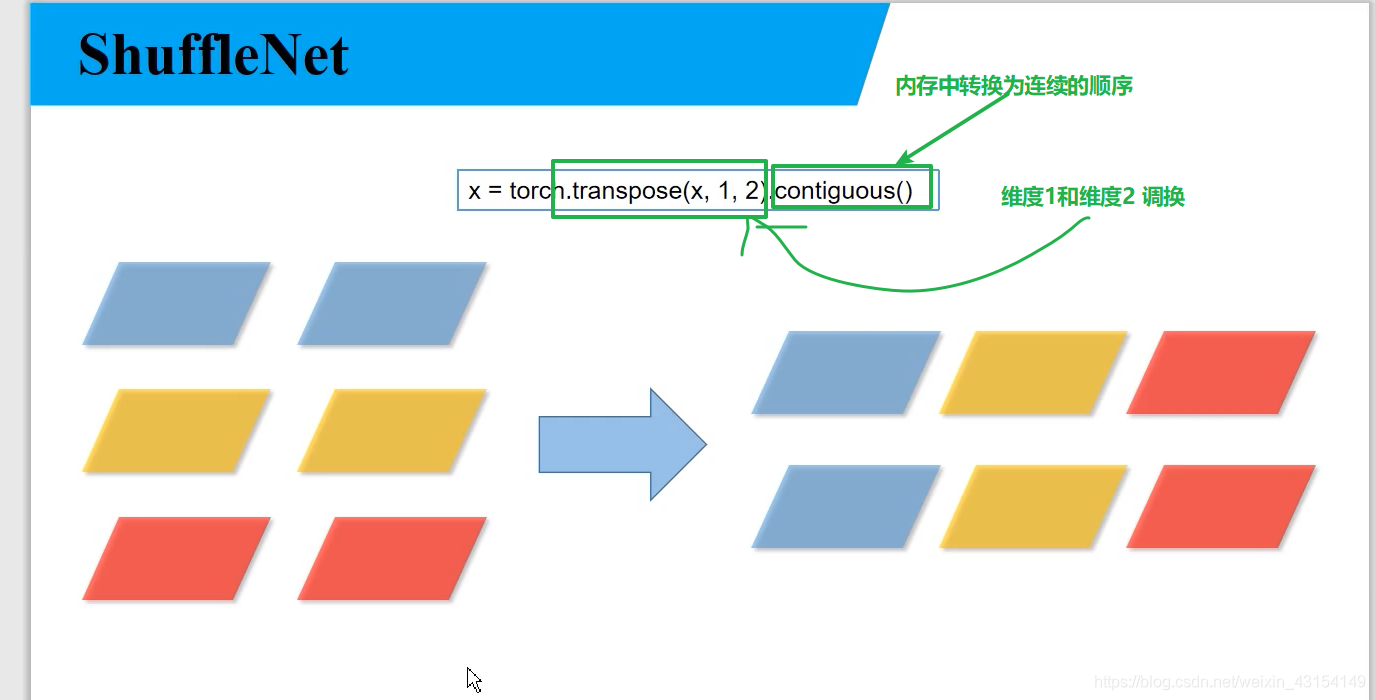
    x = torch.transpose(x, 1, 2).contiguous()

    # flatten
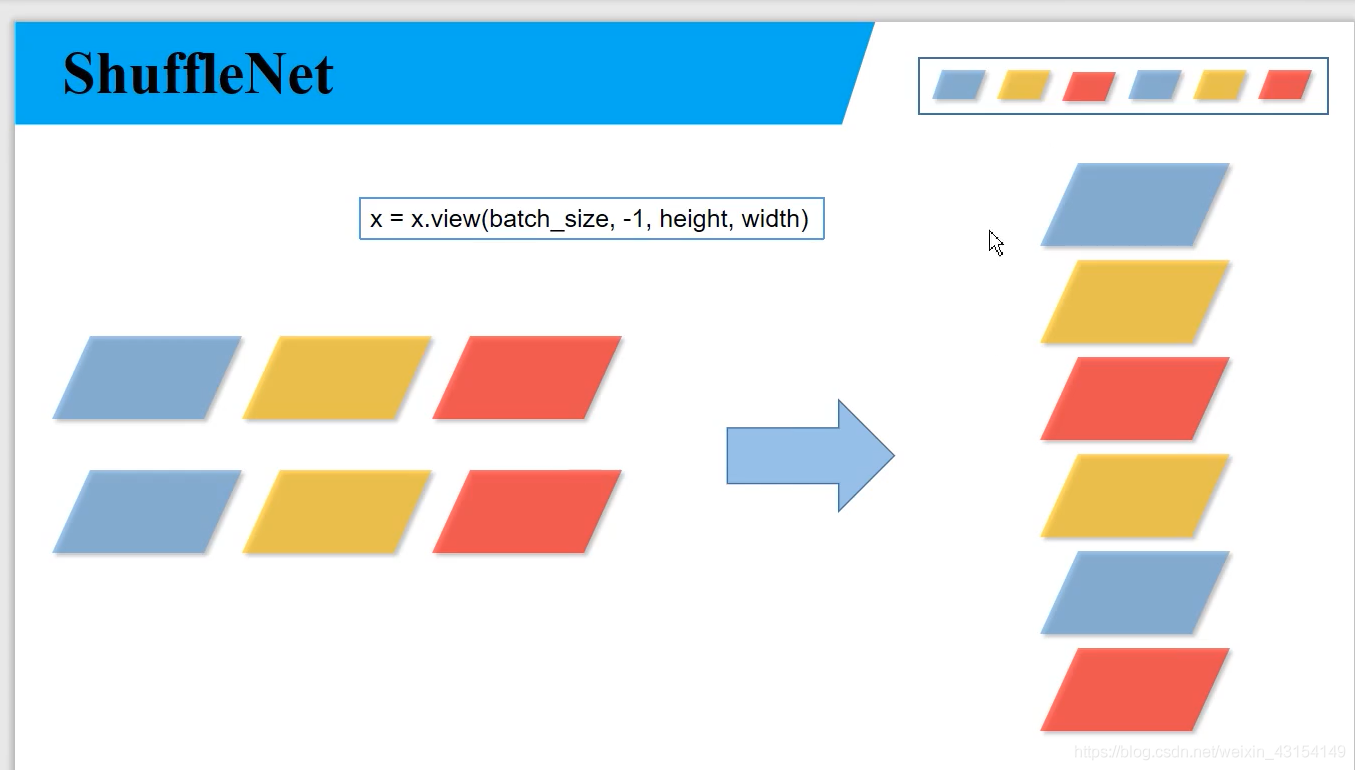
    x = x.view(batch_size, -1, height, width)

    return x

1.2 block

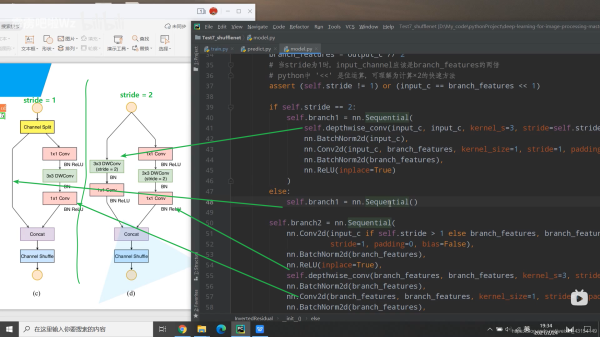
class InvertedResidual(nn.Module):
    def __init__(self, input_c: int, output_c: int, stride: int):
        super(InvertedResidual, self).__init__()

        if stride not in [1, 2]:
            raise ValueError("illegal stride value.")
        self.stride = stride

        assert output_c % 2 == 0
        branch_features = output_c // 2
        # 当stride为1时，input_channel应该是branch_features的两倍
        # python中 '<<' 是位运算，可理解为计算×2的快速方法
        assert (self.stride != 1) or (input_c == branch_features << 1)

        if self.stride == 2:
            self.branch1 = nn.Sequential(
                self.depthwise_conv(input_c, input_c, kernel_s=3, stride=self.stride, padding=1),
                nn.BatchNorm2d(input_c),
                nn.Conv2d(input_c, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
                nn.BatchNorm2d(branch_features),
                nn.ReLU(inplace=True)
            )
        else:
            self.branch1 = nn.Sequential()

        self.branch2 = nn.Sequential(
            nn.Conv2d(input_c if self.stride > 1 else branch_features, branch_features, kernel_size=1,
                      stride=1, padding=0, bias=False),
            nn.BatchNorm2d(branch_features),
            nn.ReLU(inplace=True),
            self.depthwise_conv(branch_features, branch_features, kernel_s=3, stride=self.stride, padding=1),
            nn.BatchNorm2d(branch_features),
            nn.Conv2d(branch_features, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(branch_features),
            nn.ReLU(inplace=True)
        )

    @staticmethod
    def depthwise_conv(input_c: int,
                       output_c: int,
                       kernel_s: int,
                       stride: int = 1,
                       padding: int = 0,
                       bias: bool = False) -> nn.Conv2d:
        return nn.Conv2d(in_channels=input_c, out_channels=output_c, kernel_size=kernel_s,
                         stride=stride, padding=padding, bias=bias, groups=input_c)

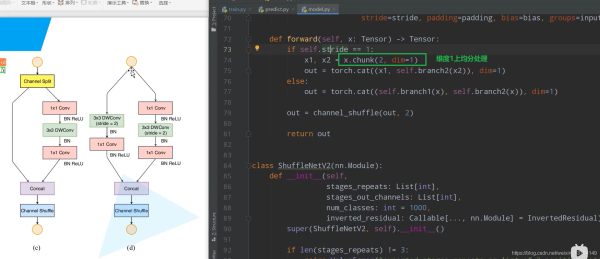
    def forward(self, x: Tensor) -> Tensor:
        if self.stride == 1:
            x1, x2 = x.chunk(2, dim=1)
            out = torch.cat((x1, self.branch2(x2)), dim=1)
        else:
            out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)

        out = channel_shuffle(out, 2)

        return out

1.3 shufflenet v2

class ShuffleNetV2(nn.Module):
    def __init__(self,
                 stages_repeats: List[int],
                 stages_out_channels: List[int],
                 num_classes: int = 1000,
                 inverted_residual: Callable[..., nn.Module] = InvertedResidual):
        super(ShuffleNetV2, self).__init__()

        if len(stages_repeats) != 3:
            raise ValueError("expected stages_repeats as list of 3 positive ints")
        if len(stages_out_channels) != 5:
            raise ValueError("expected stages_out_channels as list of 5 positive ints")
        self._stage_out_channels = stages_out_channels

        # input RGB image
        input_channels = 3
        output_channels = self._stage_out_channels[0]

        self.conv1 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=3, stride=2, padding=1, bias=False),
            nn.BatchNorm2d(output_channels),
            nn.ReLU(inplace=True)
        )
        input_channels = output_channels

        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)

        # Static annotations for mypy
        self.stage2: nn.Sequential
        self.stage3: nn.Sequential
        self.stage4: nn.Sequential

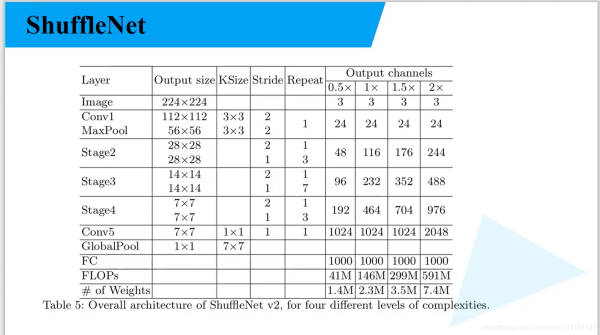
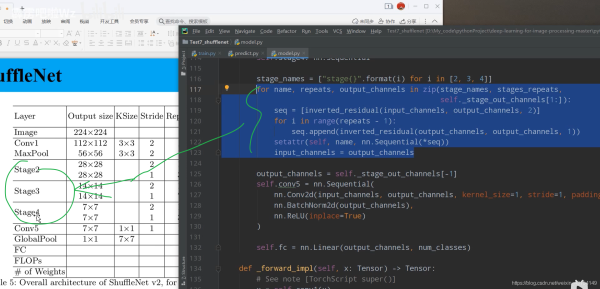
        stage_names = ["stage{}".format(i) for i in [2, 3, 4]]
        for name, repeats, output_channels in zip(stage_names, stages_repeats,
                                                  self._stage_out_channels[1:]):
            seq = [inverted_residual(input_channels, output_channels, 2)]
            for i in range(repeats - 1):
                seq.append(inverted_residual(output_channels, output_channels, 1))
            setattr(self, name, nn.Sequential(*seq))
            input_channels = output_channels

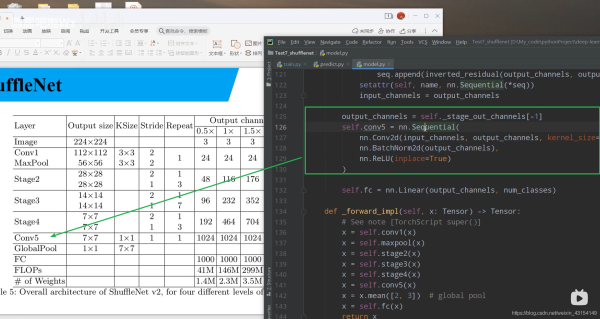
        output_channels = self._stage_out_channels[-1]
        self.conv5 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(output_channels),
            nn.ReLU(inplace=True)
        )

        self.fc = nn.Linear(output_channels, num_classes)

    def _forward_impl(self, x: Tensor) -> Tensor:
        # See note [TorchScript super()]
        x = self.conv1(x)
        x = self.maxpool(x)
        x = self.stage2(x)
        x = self.stage3(x)
        x = self.stage4(x)
        x = self.conv5(x)
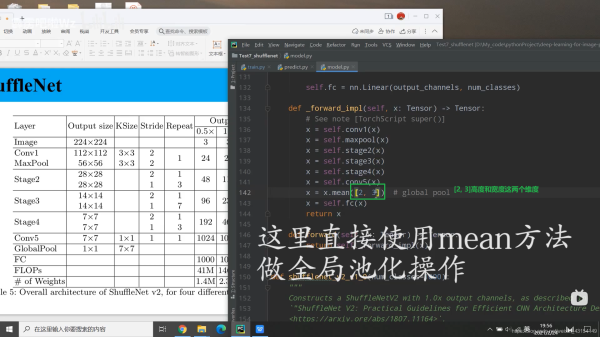
        x = x.mean([2, 3])  # global pool
        x = self.fc(x)
        return x

    def forward(self, x: Tensor) -> Tensor:
        return self._forward_impl(x)

二、train.py

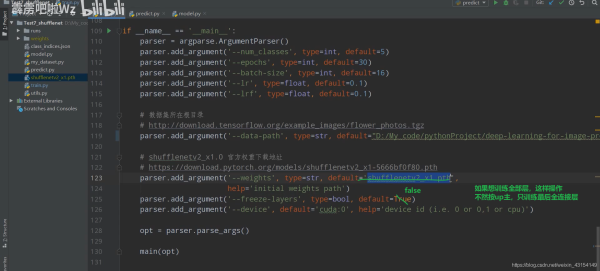
到此这篇关于Python深度学习之使用Pytorch搭建ShuffleNetv2的文章就介绍到这了,更多相关Python用Pytorch搭建ShuffleNetv2内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！