Java数据结构之图的两种搜索算法详解
目录
- 前言
- 深度优先搜索算法
- API设计
- 代码实现
- 广度优先搜素算法
- API设计
- 代码实现
- 案例应用
前言
在很多情况下,我们需要遍历图,得到图的一些性质,例如,找出图中与指定的顶点相连的所有顶点,或者判定某个顶点与指定顶点是否相通,是非常常见的需求。
有关图的搜索,最经典的算法有深度优先搜索和广度优先搜索,接下来我们分别讲解这两种搜索算法。
学习本文前请先阅读这篇文章 【数据结构与算法】图的基础概念和数据模型。
深度优先搜索算法
所谓的深度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,又有兄弟结点,那么先找子结点,然后找兄弟结点。
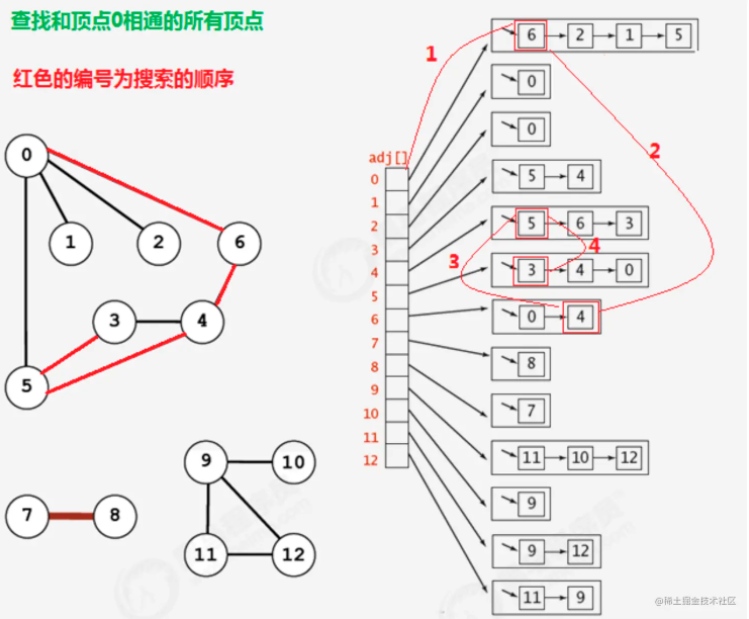
如上图所示:
由于边是没有方向的,所以,如果4和5顶点相连,那么4会出现在5的相邻链表中,5也会出现在4的相邻链表中。
为了不对顶点进行重复搜索,应该要有相应的标记来表示当前顶点有没有搜索过,可以使用一个布尔类型的数组boolean[V] marked,索引代表顶点,值代表当前顶点是否已经搜索,如果已经搜索,标记为true,
如果没有搜索,标记为false;
API设计
| 类名 | DepthFirstSearch |
|---|---|
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索2.private int count:记录有多少个顶点与s顶点相通 |
| 构造方法 | DepthFirstSearch(Graph G,int s):构造深度优先搜索对象,使用深度优先搜索找出G图中s顶点的所有相通顶点 |
| 成员方法 | 1.private void dfs(Graph G, int v):使用深度优先搜索找出G图中v顶点的所有相通顶点2.public boolean marked(int w):判断w顶点与s顶点是否相通3.public int count():获取与顶点s相通的所有顶点的总数 |
代码实现
/**
* 图的深度优先搜索算法
*
* @author alvin
* @date 2022/10/31
* @since 1.0
**/
public class DepthFirstSearch {
//索引代表顶点,值表示当前顶点是否已经被搜索
private boolean[] marked;
//记录有多少个顶点与s顶点相通
private int count;
//构造深度优先搜索对象,使用深度优先搜索找出G图中s顶点的所有相邻顶点
public DepthFirstSearch(Graph G, int s) {
//创建一个和图的顶点数一样大小的布尔数组
marked = new boolean[G.V()];
dfs(G, s);
}
//使用深度优先搜索找出G图中v顶点的所有相邻顶点
private void dfs(Graph G, int v) {
//把当前顶点标记为已搜索
marked[v] = true;
//遍历v顶点的邻接表,得到每一个顶点w
for (Integer w : G.adj(v)) {
//遍历v顶点的邻接表,得到每一个顶点w
if (!marked[w]) {
//如果当前顶点w没有被搜索过,则递归搜索与w顶点相通的其他顶点
dfs(G, w);
}
}
//相通的顶点数量+1
count++;
}
//判断w顶点与s顶点是否相通
public boolean marked(int w) {
return marked[w];
}
//获取与顶点s相通的所有顶点的总数
public int count() {
return count;
}
}
测试:
public class DepthFirstSearchTest {
@Test
public void test() {
//准备Graph对象
Graph G = new Graph(13);
G.addEdge(0,5);
G.addEdge(0,1);
G.addEdge(0,2);
G.addEdge(0,6);
G.addEdge(5,3);
G.addEdge(5,4);
G.addEdge(3,4);
G.addEdge(4,6);
G.addEdge(7,8);
G.addEdge(9,11);
G.addEdge(9,10);
G.addEdge(9,12);
G.addEdge(11,12);
//准备深度优先搜索对象
DepthFirstSearch search = new DepthFirstSearch(G, 0);
//测试与某个顶点相通的顶点数量
int count = search.count();
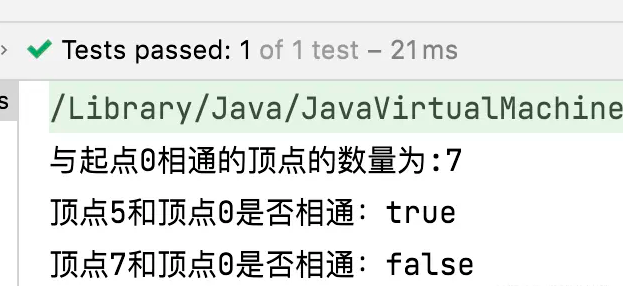
System.out.println("与起点0相通的顶点的数量为:"+count);
//测试某个顶点与起点是否相同
boolean marked1 = search.marked(5);
System.out.println("顶点5和顶点0是否相通:"+marked1);
boolean marked2 = search.marked(7);
System.out.println("顶点7和顶点0是否相通:"+marked2);
}
}
广度优先搜素算法
所谓的广度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,又有兄弟结点,那么先找兄弟结点,然后找子结点。
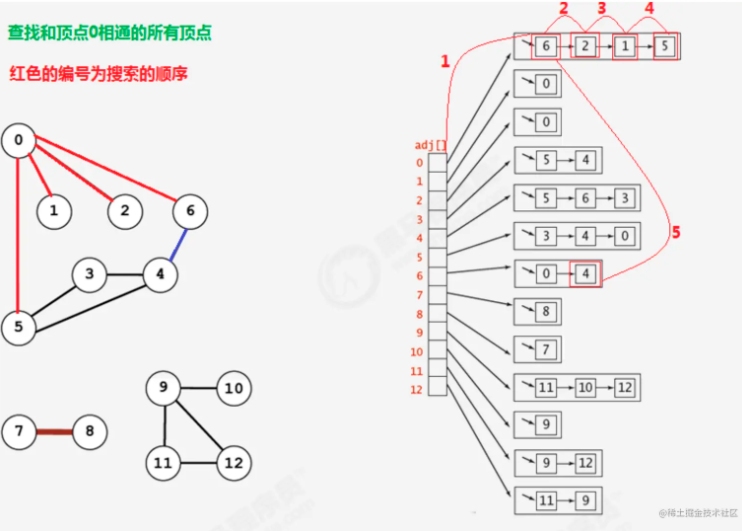
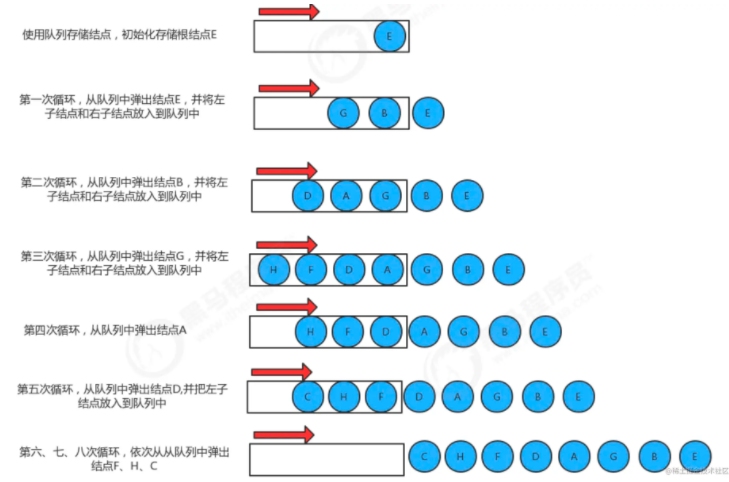
- 可以通过借助一个辅助队列实现,先将1加入到队列中
- 然后取出1,将1的相邻顶点加入到队列中
- 依次递归,如下图所示:
API设计
| 类名 | BreadthFirstSearch |
|---|---|
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索2.private int count:记录有多少个顶点与s顶点相通3.private Queue waitSearch: 用来存储待搜索邻接表的点 |
| 构造方法 | BreadthFirstSearch(Graph G,int s):构造广度优先搜索对象,使用广度优先搜索找出G图中s顶点的所有相邻顶点 |
| 成员方法 | 1.private void bfs(Graph G, int v):使用广度优先搜索找出G图中v顶点的所有相邻顶点2.public boolean marked(int w):判断w顶点与s顶点是否相通3.public int count():获取与顶点s相通的所有顶点的总数 |
代码实现
/**
* 图的广度优先搜索算法
*
* @author alvin
* @date 2022/10/31
* @since 1.0
**/
public class BreadthFirstSearch {
//索引代表顶点,值表示当前顶点是否已经被搜索
private boolean[] marked;
//记录有多少个顶点与s顶点相通
private int count;
//用来存储待搜索邻接表的点
private Queue<Integer> waitSearch;
//构造广度优先搜索对象,使用广度优先搜索找出G图中s顶点的所有相邻顶点
public BreadthFirstSearch(Graph G, int s) {
this.marked = new boolean[G.V()];
this.count = 0;
this.waitSearch = new ArrayDeque<>();
bfs(G, s);
}
//使用广度优先搜索找出G图中v顶点的所有相邻顶点
private void bfs(Graph G, int v) {
//把当前顶点v标识为已搜索
marked[v] = true;
//让顶点v进入队列,待搜索
waitSearch.add(v);
//通过循环,如果队列不为空,则从队列中弹出一个待搜索的顶点进行搜索
while (!waitSearch.isEmpty()) {
//弹出一个待搜索的顶点
Integer wait = waitSearch.poll();
//遍历wait顶点的邻接表
for (Integer w : G.adj(wait)) {
if (!marked[w]) {
bfs(G, w);
}
}
}
//让相通的顶点+1;
count++;
}
//判断w顶点与s顶点是否相通
public boolean marked(int w) {
return marked[w];
}
//获取与顶点s相通的所有顶点的总数
public int count() {
return count;
}
}
测试代码:
public class BreadthFirstSearchTest {
@Test
public void test() {
//准备Graph对象
Graph G = new Graph(13);
G.addEdge(0, 5);
G.addEdge(0, 1);
G.addEdge(0, 2);
G.addEdge(0, 6);
G.addEdge(5, 3);
G.addEdge(5, 4);
G.addEdge(3, 4);
G.addEdge(4, 6);
G.addEdge(7, 8);
G.addEdge(9, 11);
G.addEdge(9, 10);
G.addEdge(9, 12);
G.addEdge(11, 12);
//准备广度优先搜索对象
BreadthFirstSearch search = new BreadthFirstSearch(G, 0);
//测试与某个顶点相通的顶点数量
int count = search.count();
System.out.println("与起点0相通的顶点的数量为:" + count);
//测试某个顶点与起点是否相同
boolean marked1 = search.marked(5);
System.out.println("顶点5和顶点0是否相通:" + marked1);
boolean marked2 = search.marked(7);
System.out.println("顶点7和顶点0是否相通:" + marked2);
}
}
案例应用
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。目前的道路状况,9号城市和10号城市是否相通?9号城市和8号城市是否相通?
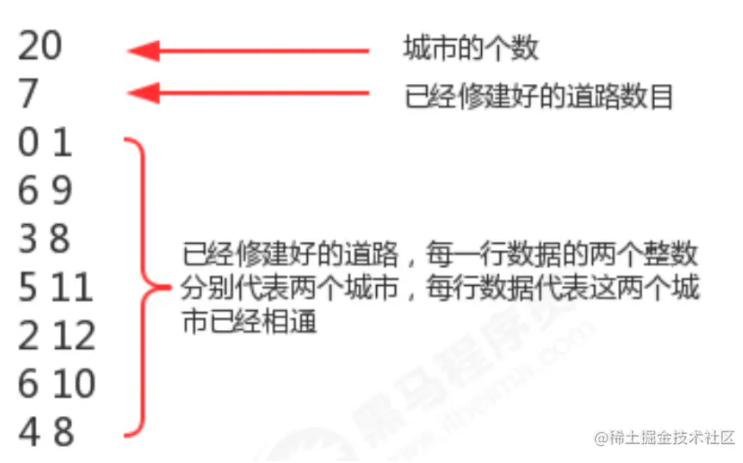
测试数据格式如上图所示,总共有20个城市,目前已经修改好了7条道路,问9号城市和10号城市是否相通?9号城市和8号城市是否相通?
解题思路:
- 创建一个图Graph对象,表示城市;
- 分别调用
addEdge(0,1),addEdge(6,9),addEdge(3,8),addEdge(5,11),addEdge(2,12),addEdge(6,10),addEdge(4,8),表示已经修建好的道路把对应的城市连接起来; - 通过Graph对象和顶点9,构建
DepthFirstSearch对象或BreadthFirstSearch对象; - 调用搜索对象的
marked(10)方法和marked(8)方法,即可得到9和城市与10号城市以及9号城市与8号城市是否相通。
代码实现:
public class TrafficProjectGraph {
public static void main(String[] args) throws Exception{
//城市数量
int totalNumber = 20;
Graph G = new Graph(totalNumber);
//添加城市的交通路线
G.addEdge(0,1);
G.addEdge(6,9);
G.addEdge(3,8);
G.addEdge(5,11);
G.addEdge(2,12);
G.addEdge(6,10);
G.addEdge(4,8);
//构建一个深度优先搜索对象,起点设置为顶点9
DepthFirstSearch search = new DepthFirstSearch(G, 9);
//调用marked方法,判断8顶点和10顶点是否与起点9相通
System.out.println("顶点8和顶点9是否相通:"+search.marked(8));
System.out.println("顶点10和顶点9是否相通:"+search.marked(10));
}
}
结果:

以上就是Java数据结构之图的两种搜索算法详解的详细内容,更多关于Java图搜索算法的资料请关注我们其它相关文章!
赞 (0)

