Java面试题冲刺第二十三天--算法(2)

目录

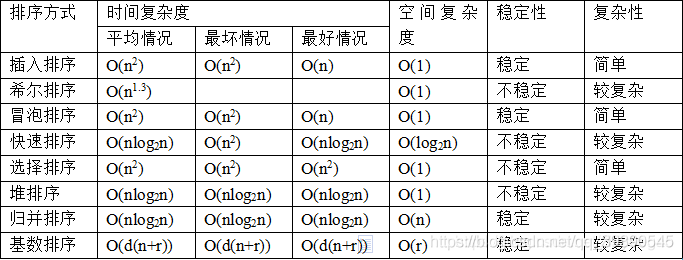
• 面试题1：你说一下常用的排序算法都有哪些？
• 追问1：谈一谈你对快排的理解吧
• 追问2：说一下快排的算法原理
• 追问3：来吧！给我手敲一个快排
• 面试题2：来！再给我手撸一个Spring
• 追问1：哦，咳咳…说一下构成递归的前提条件有啥？
• 追问2：递归都有哪些优缺点？
• 追问3：给我手写一个简单的递归算法的实现吧
• 面试题3： 10亿个数中找出最大的100000个数（top K问题）
• 总结

面试题1：你说一下常用的排序算法都有哪些？

追问1：谈一谈你对快排的理解吧

快速排序，顾名思义就是一种以效率快为特色的排序算法，快速排序（Quicksort）是对冒泡排序的一种改进。由英国计算机专家:托尼·霍尔（Tony Hoare）在1960年提出。

从排序数组中找出一个数，可以随机取，也可以取固定位置，一般是取第一个或最后一个，称为基准数。然后将比基准小的排在左边，比基准大的放到右边；

如何放置呢，就是和基准数进行交换，交换完左边都是比基准小的，右边都是比较基准大的，这样就将一个数组分成了两个子数组，然后再按照同样的方法把子数组再分成更小的子数组，直到不能分解（子数组只有一个值）为止。以此达到整个数据变成有序序列。

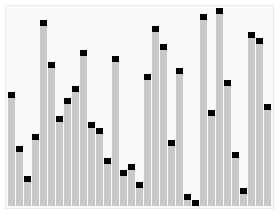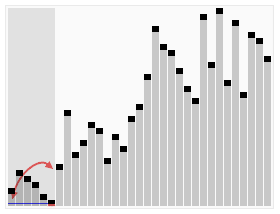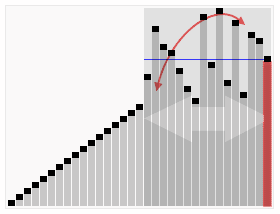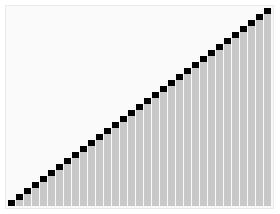
快速排序采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)，现在各种语言中自带的排序库很多使用的都是快速排序。

空间复杂度

快速排序是一种原地排序，只需要一个很小的栈作为辅助空间，空间复杂度为O(log2n)，所以适合在数据集比较大的时候使用。

时间复杂度

时间复杂度比较复杂，最好的情况是O(n)，最差的情况是O(n2)，所以平时说的O(nlogn)，为其平均时间复杂度。

• O(n)：理想的情况，每次划分所选择的中间数恰好将当前序列几乎等分，经过log2n趟划分，便可得到长度为1的子表。这样，整个算法的时间复杂度为O(nlog2n)。
• O(n2)：最坏的情况，每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度-1。这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法的时间复杂度为O(n2)。

追问2：说一下快排的算法原理

算法步骤

• 选定一个基准数（一般取第一位数字）作为中心点（Pivot）；
• 将大于Pivot的数字放到Pivot的左边；
• 将小于Pivot的数字放到Pivot的右边；
• 第一次排序结束后，分别对左右子序列继续递归重复前三步操作，直到左右子序列长度只有单个元素为止。

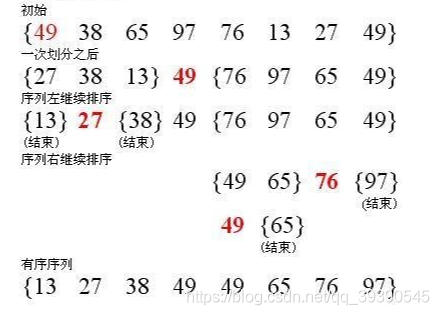
demo示例

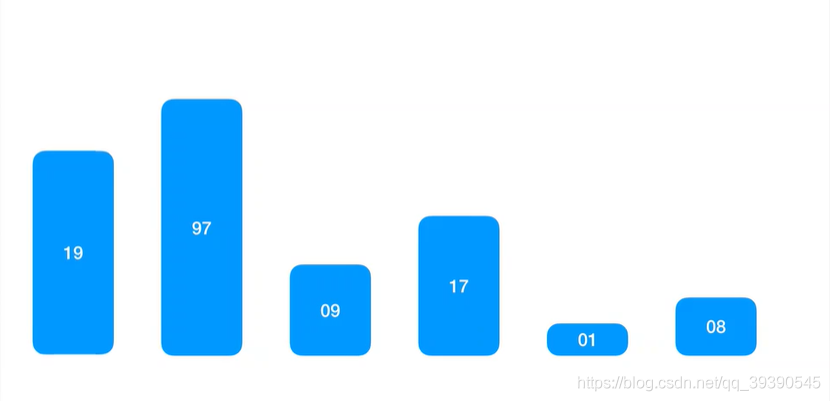
实例数组：arr[] = {19，97，9，17，1，8}；

取出基准数Pivot，以该值为中心轴。

快速排序中的规则：右边有坑，就从左边Arr[L + n]取值来填，反之左边有坑，则从右边Arr[R - n]取值来填；

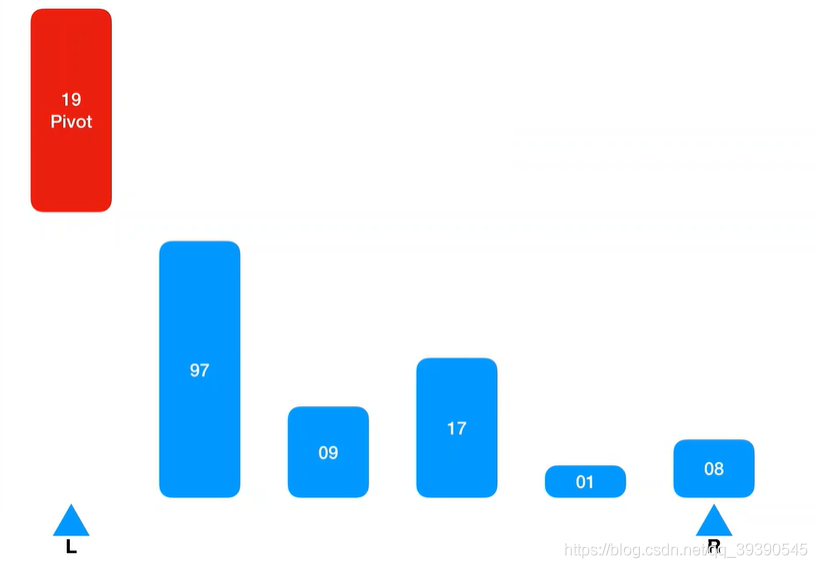
从左边取的基准值，左边的Arr[L]就空出来了，则先从右侧取值来填，从最右侧下标开始，在Arr[R] 取到第一个值“8”；

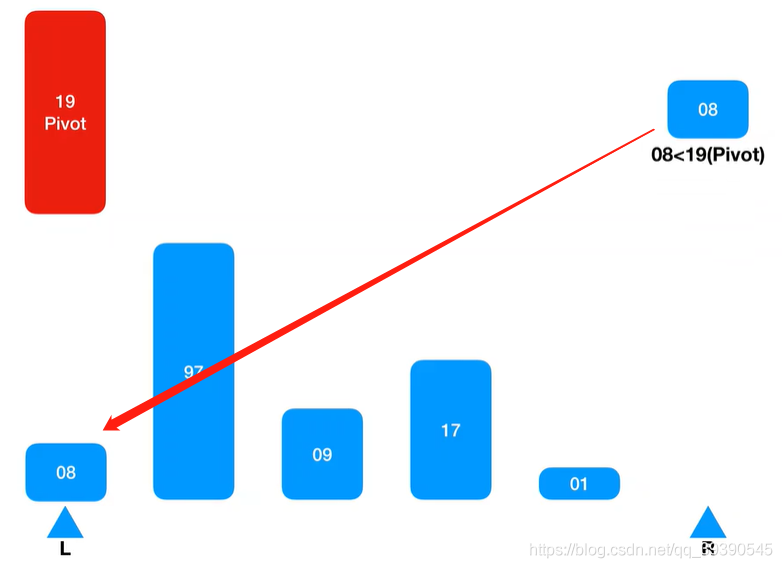
将取到的Arr[R]与基准值比较，发现小于基准值，则插入到Arr[R]，占到了基准值Pivot的位置上。

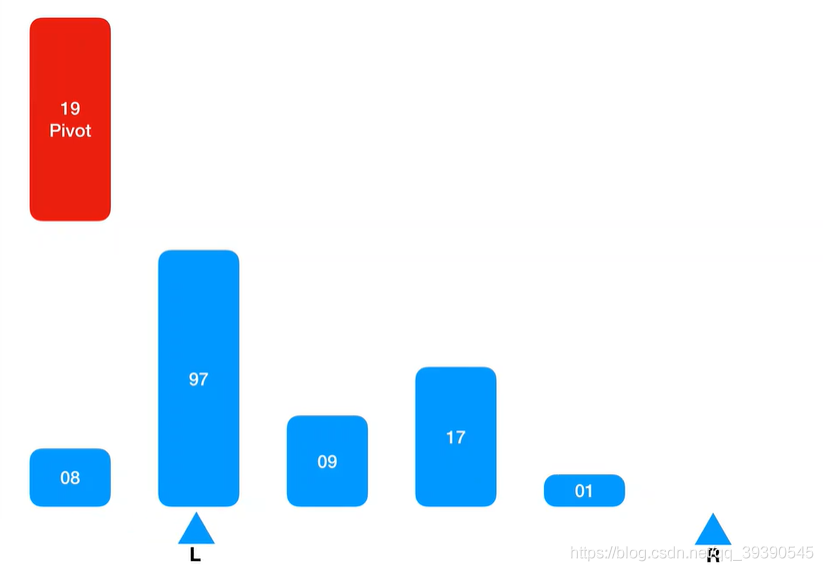
然后从Arr[L+1]的位置取出值，继续向右匹配并排序，将匹配到的值（匹配规则如下）插入到右侧Arr[R]的空位置上；

匹配规则：大于基准值的插入到Arr[R]，如果小于，则直接忽略并跳过，继续向右取值，直到坐标L和坐标R重合。

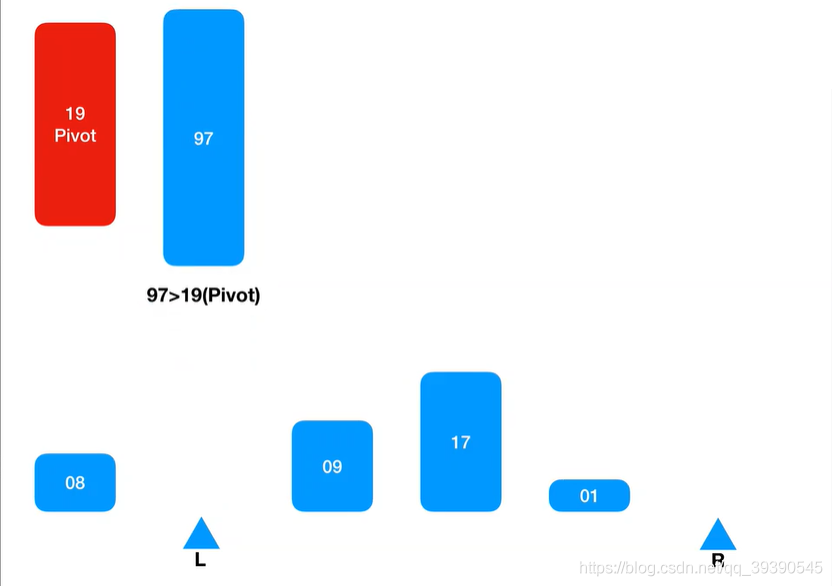
发现取出的值大于Pivot（基准值），则将其插入到Arr[R]。

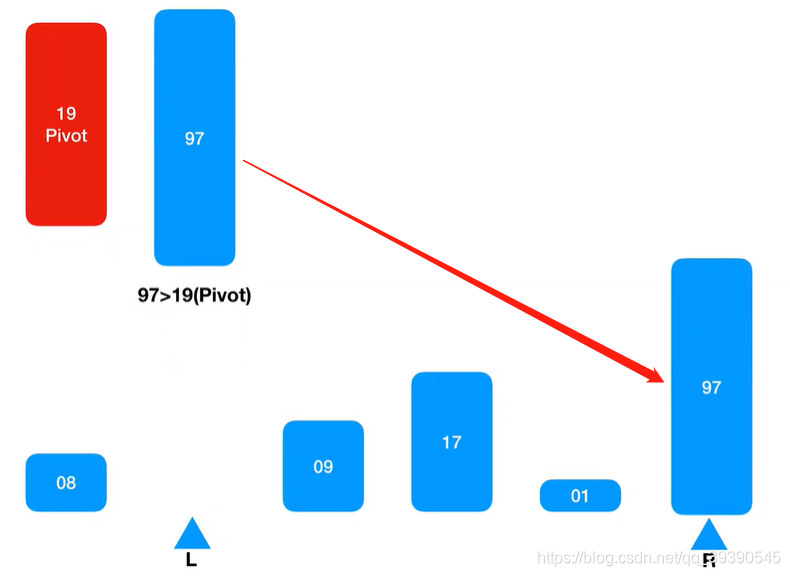
左边有坑，从右边Arr[R-1]继续匹配，Arr[R-1] = 1，小于基准值，则插入到Arr[L]的坑中；

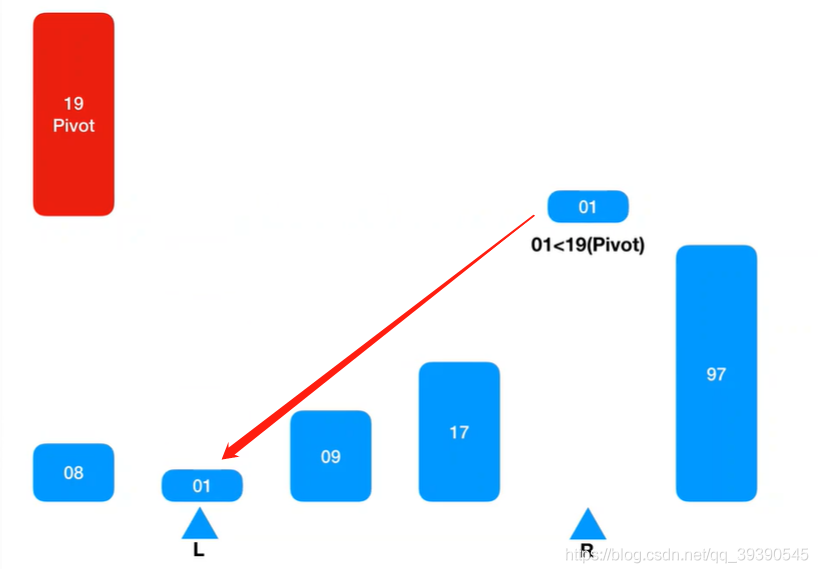
右边有坑了，继续从左边取值继续匹配，则取到Arr[L+1] = 9,小于基准值，则忽略并跳过，继续找Arr[L + 1]继续匹配。

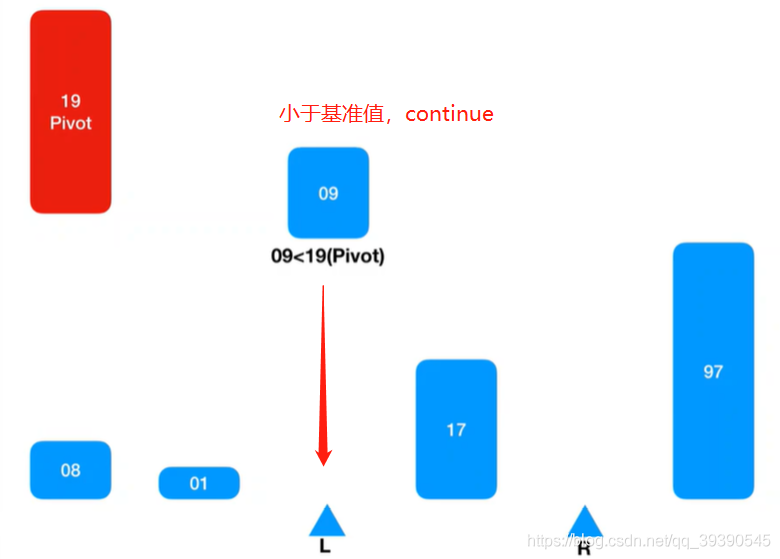
继续从左边坐标 + 1 取值继续匹配，则取到Arr[L] = 17，又小于基准值，则忽略并跳过，继续找Arr[L + 1]继续匹配。

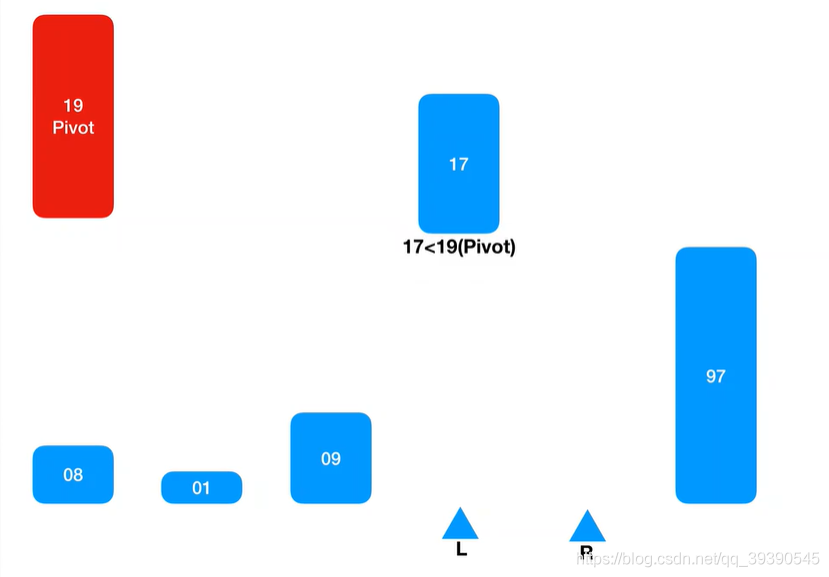
最后L坐标和R坐标重合了，将Pivot基准值填入

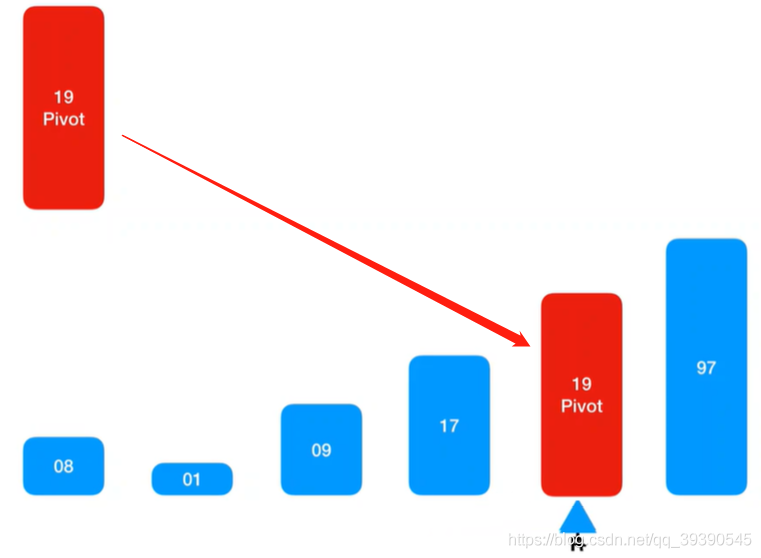
至此，快速排序第一轮完整流程结束，分出了左右子序列，左边都是小于Pivot基准值的，右边都是大于Pivot基准值的。

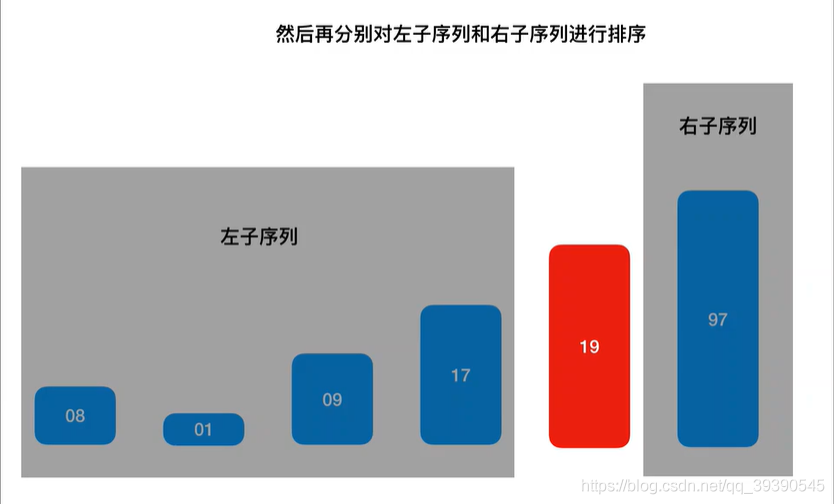
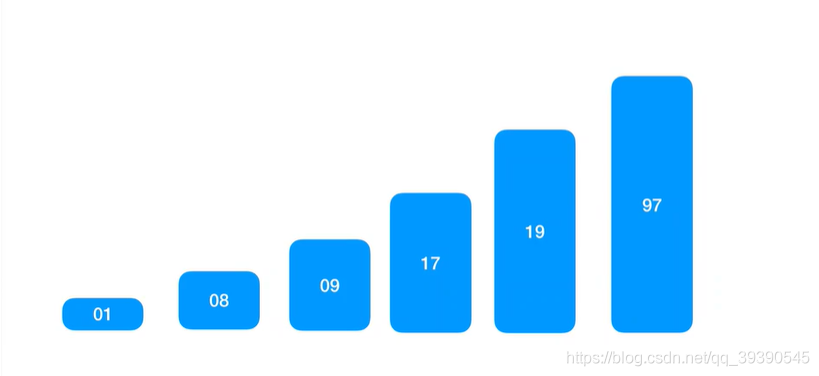
继续对左、右子序列递归进行处理，一直缩小到左、右都是一个值，则快速排序结束，最终得出顺序数组{1,8,9,17,19,97}；中间递归流程这里不再赘述。

追问3：来吧！给我手敲一个快排

package com.softsec.demo;
/**
 * Created with IDEA
 *
 * @Author Chensj
 * @Date 2020/5/17 19:04
 * @Description
 * @Version 1.0
 */
public class quickSortDemo {
    public static void main(String[] args) {
        // 创建测试数组
        int[] arr = new int[]{19,97,9,17,1,8};
        System.out.println("排序前：");
        showArray(arr); // 打印数组
        // 调用快排接口
        quickSort(arr);
        System.out.println("\n" + "排序后：");
        showArray(arr);// 打印数组
    }
    /**
     * 快速排序
     * @param array
     */
    public static void quickSort(int[] array) {
        int len;
        if(array == null
                || (len = array.length) == 0
                || len == 1) {
            return ;
        }
        sort(array, 0, len - 1);
    }
    /**
     * 快排核心算法，递归实现
     * @param array
     * @param left
     * @param right
     */
    public static void sort(int[] array, int left, int right) {
        if(left > right) {
            return;
        }
        // base中存放基准数
        int base = array[left];
        int i = left, j = right;
        while(i != j) {
            // 顺序很重要，先从右边开始往左找，直到找到比base值小的数
            while(array[j] >= base && i < j) {
                j--;
            }
            // 再从左往右边找，直到找到比base值大的数
            while(array[i] <= base && i < j) {
                i++;
            }
            // 上面的循环结束表示找到了位置或者(i>=j)了，交换两个数在数组中的位置
            if(i < j) {
                int tmp = array[i];
                array[i] = array[j];
                array[j] = tmp;
            }
        }
        // 将基准数放到中间的位置（基准数归位）
        array[left] = array[i];
        array[i] = base;
        // 递归，继续向基准的左右两边执行和上面同样的操作
        // i的索引处为上面已确定好的基准值的位置，无需再处理
        sort(array, left, i - 1);
        sort(array, i + 1, right);
    }
    /**
     * 数组打印
     * @param num
     */
    private static void showArray(int[] num) {
        for (int i = 0; i < num.length; i++) {
            System.out.print(num[i] + " ");
        }
    }
}

面试题2：来！再给我手撸一个Spring

我：？？？

追问1：哦，咳咳…说一下构成递归的前提条件有啥？

函数内部调用的自身函数的编程技巧称为递归（recursion）。

构成递归的条件：

• 子问题须与原始问题为同样的事，且更为简单；
• 不能无限制地调用本身，须有个出口，化简为非递归状况处理。

追问2：递归都有哪些优缺点？

优点：

1.简洁

2.在树的前序，中序，后序遍历算法中，递归的实现明显要比循环简单得多。

缺点：

1.递归由于是函数调用自身，而函数调用是有时间和空间的消耗的：每一次函数调用，都需要在内存栈中分配空间以保存参数、返回地址以及临时变量，而往栈中压入数据和弹出数据都需要时间。（效率）

2.递归中很多计算都是重复的，由于其本质是把一个问题分解成两个或者多个小问题，多个小问题存在相互重叠的部分，则存在重复计算，如fibonacci斐波那契数列的递归实现。（效率）

3.调用栈可能会溢出，其实每一次函数调用会在内存栈中分配空间，而每个进程的栈的容量是有限的，当调用的层次太多时，就会超出栈的容量，从而导致栈溢出。（性能）

追问3：给我手写一个简单的递归算法的实现吧

例如递归计算一下n的阶乘

package com.softsec;
/**
 * 递归计算n的阶乘
 * @author Chenhh
 */
public class demo {
    public static void main(String[] args) {
        System.out.println(recursion(5));
    }
    /**
     * 递归计算n的阶乘
     */
    private static int recursion(int n) {
        if (n <1) {
            throw new IllegalArgumentException("参数必须大于0");
        } else if (n == 1) {
            return 1;
        } else {
            return n * recursion(n - 1);
        }
    }
}

面试题3： 10亿个数中找出最大的100000个数（top K问题）

先拿100000个数建堆，然后一次添加剩余元素，如果大于堆顶的数（100000中最小的），将这个数替换堆顶，并调整结构使之仍然是一个最小堆，这样，遍历完后，堆中的100000个数就是所需的最大的100000个。建堆时间复杂度是O(m)，算法的时间复杂度为1次建堆时间+n次堆调整时间=O(m+nlogm)=O(nlogm)（n为10亿，m为100000）。

优化的方法：可以把所有10亿个数据分组存放，比如分别放在1000个文件中。这样处理就可以分别在每个文件的10^6个数据中找出最大的100000个数，合并到一起在再找出最终的结果。

top K问题

在大规模数据处理中，经常会遇到的一类问题：在海量数据中找出出现频率最好的前k个数，或者从海量数据中找出最大的前k个数，这类问题通常被称为top K问题。例如，在搜索引擎中，统计搜索最热门的10个查询词；在歌曲库中统计下载最高的前10首歌等。

针对top K类问题，通常比较好的方案是分治+Trie树/hash+小顶堆（就是上面提到的最小堆），即先将数据集按照Hash方法分解成多个小数据集，然后使用Trie树活着Hash统计每个小数据集中的query词频，之后用小顶堆求出每个数据集中出现频率最高的前K个数，最后在所有top K中求出最终的top K。

对于有10亿个整数，如何找出其中最大的10万个这个问题

最容易想到的方法是将数据全部排序，然后在排序后的集合中进行查找，最快的排序算法的时间复杂度一般为O（nlogn），如快速排序。但是如果按每个int类型占4个字节，10亿个整数就要占用4G的存储空间，对于一些java运行内存小于4G的计算机而言，直接OOM（out of memory）了。其实即使内存能够满足要求（我机器内存都是8GB），该方法也并不高效，因为题目的目的是寻找出最大的100000个数即可，而排序却是将所有的元素都排序了，做了很多的无用功。

第二种方法为局部淘汰法，该方法与排序方法类似，用一个容器保存前100000个数，然后将剩余的所有数字——与容器内的最小数字相比，如果所有后续的元素都比容器内的100000个数还小，那么容器内这个100000个数就是最大100000个数。如果某一后续元素比容器内最小数字大，则删掉容器内最小元素，并将该元素插入容器，最后遍历完这1亿个数，得到的结果容器中保存的数即为最终结果了。此时的时间复杂度为O（n+m^2），其中m为容器的大小，即100000。

第三种方法是分治法，将10亿个数据分成1000份，每份100万个数据，找到每份数据中最大的100000个，最后在剩下的1000 * 100000个数据里面找出最大的100000个。如果100万数据选择足够理想，那么可以过滤掉1亿数据里面99%的数据。100万个数据里面查找最大的100000个数据的方法如下：用快速排序的方法，将数据分为2堆，如果大的那堆个数N大于100000个，继续对大堆快速排序一次分成2堆，如果大的那堆个数N大于100000个，继续对大堆快速排序一次分成2堆，如果大堆个数N小于100000个，就在小的那堆里面快速排序一次，找第100000-n大的数字；递归以上过程，就可以找到第10w大的数。参考上面的找出第10w大的数字，就可以类似的方法找到前100000大数字了。此种方法需要每次的内存空间为10^6*4=4MB，一共需要101次这样的比较。

第四种方法是Hash法。如果这1亿个书里面有很多重复的数，先通过Hash法，把这10亿个数字去重复，这样如果重复率很高的话，会减少很大的内存用量，从而缩小运算空间，然后通过分治法或最小堆法查找最大的100000个数。

第五种方法采用最小堆。首先读入前100000个数来创建大小为100000的最小堆，建堆的时间复杂度为O(m)（m为数组的大小即为100000），然后遍历后续的数字，并于堆顶（最小）数字进行比较。如果比最小的数小，则继续读取后续数字；如果比堆顶数字大，则替换堆顶元素并重新调整堆为最小堆。整个过程直至10亿个数全部遍历完为止。然后按照中序遍历的方式输出当前堆中的所有100000个数字。该算法的时间复杂度为O（nmlogm），空间复杂度是100000（常数）。

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容！