C语言实现九大排序算法的实例代码

直接插入排序

将数组分为两个部分，一个是有序部分，一个是无序部分。从无序部分中依次取出元素插入到有序部分中。过程就是遍历有序部分，实现起来比较简单。

#include <stdio.h>

void insertion_sort(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  int data = arr[i];
  int j = 0;
  while (arr[j] < arr[i]) {
   j++;
  }
  for (int k = i; k >= j + 1; k--) {
   arr[k] = arr[k - 1];
  }
  arr[j] = data;
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int arr[7] = {8, 2, 6, 0, 5, 7, 4};
 insertion_sort(arr, 7);
 print_array(arr, 7);
 return 0;
}

折半插入排序

折半插入再直接插入上有改进，用折半搜索替换遍历数组，在数组长度大时能够提升查找性能。其本质还是从无序部分取出元素插入到有序部分中。

#include <stdio.h>

void binary_insertion_sort(int arr[], int array_length) {
 int i, j, low = 0, high = 0, mid;
 int temp = 0;
 for (i = 1; i < array_length; i++) {
  low = 0;
  high = i - 1;
  temp = arr[i];
  while (low <= high) {
   mid = (low + high) / 2;
   if (arr[mid] > temp) {
    high = mid - 1;
   } else {
    low = mid + 1;
   }
  }
  for (j = i; j > low; j--) {
   arr[j] = arr[j - 1];
  }
  arr[low] = temp;
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int brr[5] = {2, 6, 0, 5, 7};
 binary_insertion_sort(brr, 5);
 print_array(brr, 5);
 return 0;
}

希尔排序

希尔排序的核心就是根据步长分组，组内进行插入排序。关于步长的选取，第一次步长取元素的个数，后面每次取原来步长的一半。

希尔排序属于插入排序的一种。

#include <stdio.h>

void shell_sort(int arr[], int array_length) {
 int step = array_length / 2;
 while (step >= 1) {
  for (int i = 0; i < array_length; i += step) {
   int data = arr[i];
   int j = 0;
   while (arr[j] < arr[i]) {
    j++;
   }
   for (int k = i; k >= j + 1; k--) {
    arr[k] = arr[k - 1];
   }
   arr[j] = data;
  }
  step = step / 2;
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int crr[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
 shell_sort(crr, 10);
 print_array(crr, 10);
 return 0;
}

冒泡排序

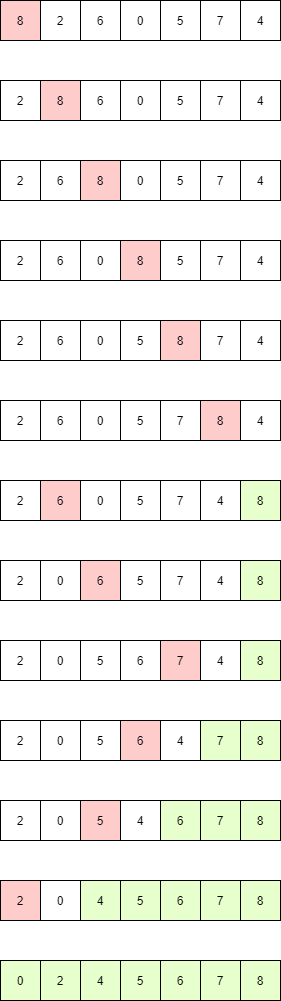
冒泡的特点是两两交换。通过交换把最大的元素交换到后面去了，每次循环遍历都把无序部分最大的“沉”到后面去。小数上“浮”和大数下“沉”其实没有差别，都能实现冒泡。

#include <stdio.h>

void bubble_sort(int arr[], int array_length) {
 for (int i = 0; i < array_length - 1; ++i) {
  for (int j = 0; j < array_length - i - 1; ++j) {
   if (arr[j] > arr[j + 1]) {
    int temp = arr[j];
    arr[j] = arr[j + 1];
    arr[j + 1] = temp;
   }
  }
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int drr[7] = {8, 2, 6, 0, 5, 7, 4};
 bubble_sort(drr, 7);
 print_array(drr, 7);
 return 0;
}

快速排序

快排的精髓在于选定一个标准（通常选数组的第一个元素），然后将所有元素根据标准分为小于和大于两个部分，然后这两个部分再选取标准，继续递归下去，不难想象最终排序结果是整体有序的。

#include <stdio.h>

int getStandard(int arr[], int low, int high) {
 int flag = arr[low];
 while (low < high) {
  while (low < high && arr[high] >= flag) {
   high--;
  }
  if (low < high) {
   arr[low] = arr[high];
  }
  while (low < high && arr[low] <= flag) {
   low++;
  }
  if (low < high) {
   arr[high] = arr[low];
  }
 }
 arr[low] = flag;
 return low;
}

void quick_sort(int arr[], int low, int high) {
 if (low < high) {
  int pos = getStandard(arr, low, high);
  quick_sort(arr, low, pos - 1);
  quick_sort(arr, pos + 1, high);
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int err[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
 quick_sort(err, 0, 9);
 print_array(err, 10);
 return 0;
}

直接选择排序

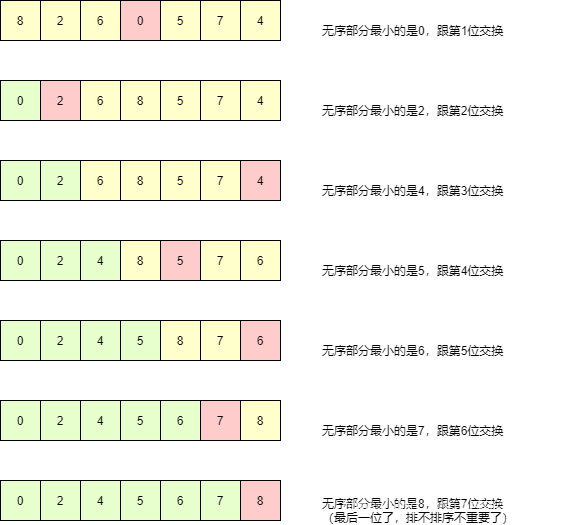
如其名，直接选择一个最小的放到最前面，但是遍历往往导致效率较低。

#include <stdio.h>

void select_sort(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  int min_pos = i;
  for (int j = i; j < array_length; ++j) {
   if (arr[min_pos] > arr[j])
    min_pos = j;
  }
  int temp = arr[min_pos];
  arr[min_pos] = arr[i];
  arr[i] = temp;
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int frr[7] = {8, 2, 6, 0, 5, 7, 4};
 select_sort(frr, 7);
 print_array(frr, 7);
 return 0;
}

堆排序

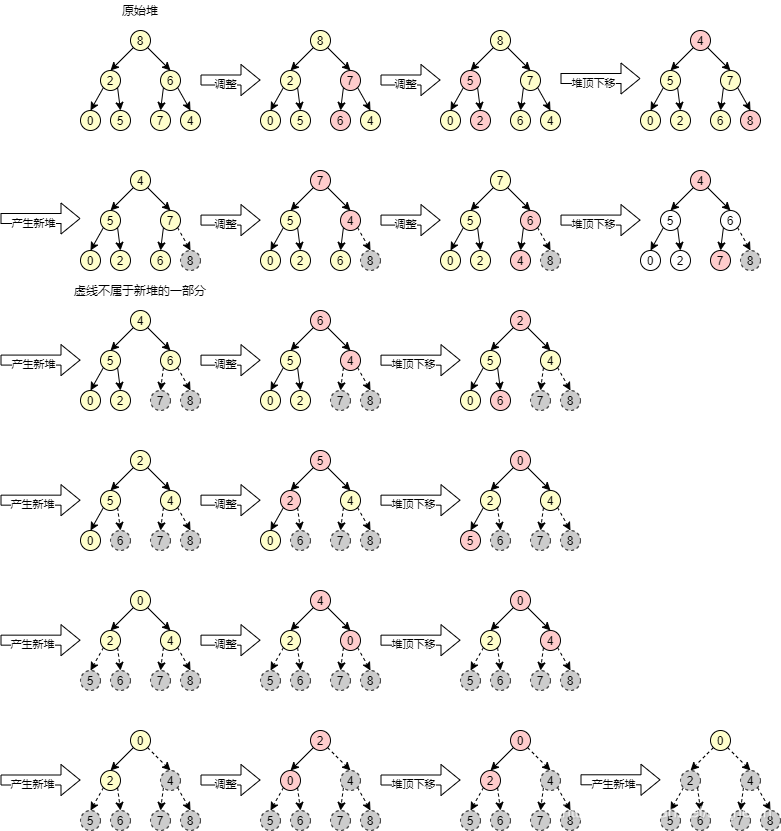
将数组转换为一颗完全二叉树。任意一个父节点大于它的子节点，这样的完全二叉树叫做大顶堆；与之相反的，任意一个父节点小于它的子节点，这样的完全二叉树叫做小顶堆。

堆排序的精华就在于把元素个数为n的完全二叉树转换为大顶堆，然后把堆顶和最后一个元素交换，此时产生了一个元素个数为n-1的完全二叉树，然后再转换为大顶堆，继续把堆顶和最后一个元素交换。循环往复就实现了排序。其实质还是选择排序，每次选出一个最大的，和最后一个交换，不过完全二叉树中选最大元素比遍历数组会快很多。

#include <stdio.h>

void heap_adjust(int arr[], int n) {
 for (int i = n / 2; i >= 1; i--) {
  if (arr[i - 1] < arr[2 * i - 1]) {
   int temp = arr[i - 1];
   arr[i - 1] = arr[2 * i - 1];
   arr[2 * i - 1] = temp;
  }
  if (arr[i - 1] < arr[2 * i] && (2 * i) < n) {
   int temp = arr[i - 1];
   arr[i - 1] = arr[2 * i];
   arr[2 * i] = temp;
  }
 }
}

void heap_sort(int arr[], int array_length) {
 int n = array_length;
 do {
  heap_adjust(arr, n);
  int temp = arr[0];
  arr[0] = arr[n - 1];
  arr[n - 1] = temp;
 } while (n--);
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int grr[7] = {8, 2, 6, 0, 5, 7, 4};
 heap_sort(grr, 7);
 print_array(grr, 7);
 return 0;
}

归并排序

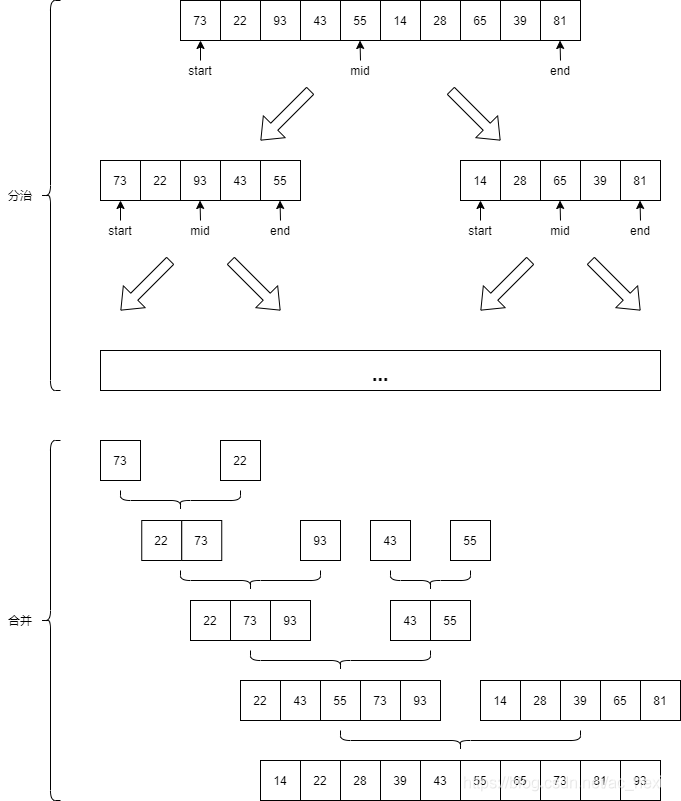
归并的思想在于对复杂问题的分治，打散到最小长度后然后再进行合并操作。假设有两个数组A、B，指针i指向A的头部，指针j指向B的头部，两边同时进行遍历，找到一个小的就放到数组里面，对应指针后移一位，这样就能够保证合并后的数组是有序的。

#include <stdio.h>
#include <malloc.h>

void merge(int arr[], int start, int mid, int end) {
 int *new_array = (int *) malloc(sizeof(int) * (end - start + 1));
 int i = start;
 int j = mid + 1;
 int k = 0;
 while (i <= mid && j <= end) {
  if (arr[i] < arr[j]) {
   new_array[k++] = arr[i++];
  } else {
   new_array[k++] = arr[j++];
  }
 }
 while (i <= mid) {
  new_array[k++] = arr[i++];
 }
 while (j <= end) {
  new_array[k++] = arr[j++];
 }
 for (int l = 0; l < k; ++l) {
  arr[start + l] = new_array[l];
 }
 free(new_array);
}

void merge_sort(int arr[], int start, int end) {
 int mid = (start + end) / 2;
 if (start >= end) {
  return;
 }
 merge_sort(arr, start, mid);
 merge_sort(arr, mid + 1, end);
 merge(arr, start, mid, end);
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int hrr[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
 merge_sort(hrr, 0, 9);
 print_array(hrr, 10);
 return 0;
}

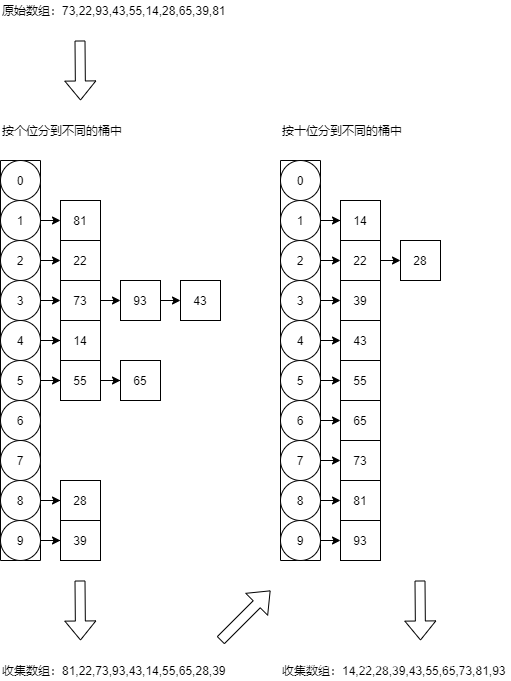
基数排序

先按照个位排序将所有数字分配到0-9这10个桶里面，然后再按照桶的顺序收集起来；再按照十位排序，同样的步骤……

基础排序的本质是对每一位进行排序，对每一位进行排序后就能保证这一个数整体的大小是按照顺序排列的。

#include <stdio.h>
#include <malloc.h>

int get_num(int number, int pos) {
 int num = 0;
 while (pos--) {
  num = number % 10;
  number = number / 10;
 }
 return num;
}

void radix_sort(int arr[], int array_length) {
 int *bucket[10];
 for (int i = 0; i < 10; ++i) {
  bucket[i] = (int *) malloc(sizeof(int) * array_length + 1);
  bucket[i][0] = 0;//桶的第一位保存桶中元素个数
 }
 for (int b = 1; b <= 31; ++b) {
  for (int i = 0; i < array_length; ++i) {
   int num = get_num(arr[i], b);//计算每个位上的数字（个位、十位、百位...）
   int index = ++bucket[num][0];//计算下标
   bucket[num][index] = arr[i];//保存到桶中
  }
  for (int i = 0, k = 0; i < 10; i++) {
   for (int j = 1; j <= bucket[i][0]; ++j) {
    arr[k++] = bucket[i][j];//从桶里面按顺序取出来
   }
   bucket[i][0] = 0;//下标清零
  }
 }
}

void print_array(int arr[], int array_length) {
 for (int i = 0; i < array_length; ++i) {
  printf("%d ", arr[i]);
 }
 printf("\n");
}

int main() {
 int irr[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
 radix_sort(irr, 10);
 print_array(irr, 10);
 return 0;
}

总结

到此这篇关于C语言实现九大排序算法的文章就介绍到这了,更多相关C语言九大排序算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！