关于C++中二分法详解

目录

• 一、整数二分
• 1.整数二分模板
• 2.求解二分问题的思路
• 3.练习
• 二、浮点数二分
• 1.浮点数二分模板
• 2.练习
• 三、总结

一、整数二分

单调性与二分的关系：有单调性一定可以二分，用二分不一定是单调性。二分的本质不是单调性而是边界点（找符合条件的最小的数或者最大的数）整数二分是求红色范围的右端点 或者 绿色范围的左端点

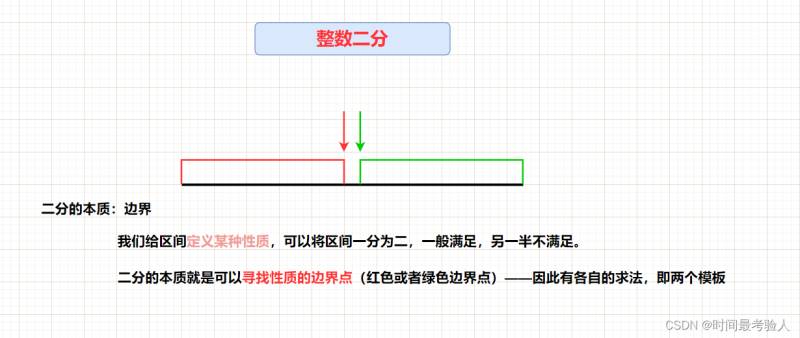
1.整数二分模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

【模板1】

1、求红色边界点

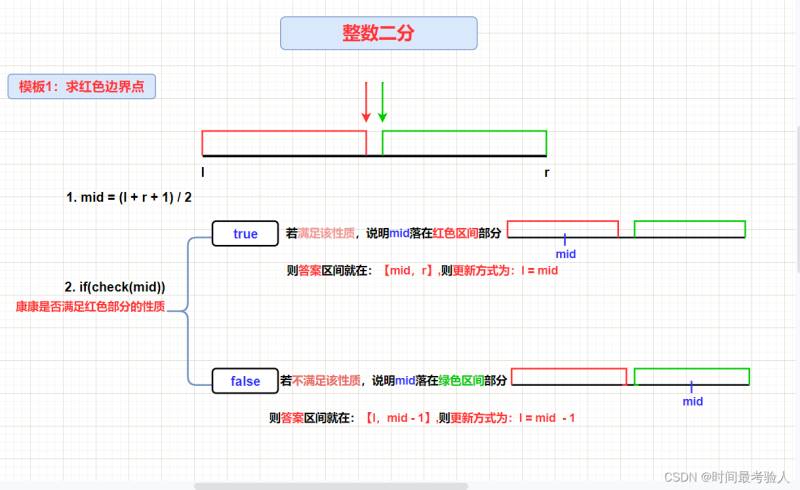
注： + 1原因：

/ 是向下取整，当l与r只相差1的时候，即 l = r - 1，最终的结果mid = l（即结果不变还是l）,补上1之后 mid = r，再次循环之后l = r 即[r , r]，最终结束循环。如果不补1将会出现死循环。

【模板2】

求绿色边界点

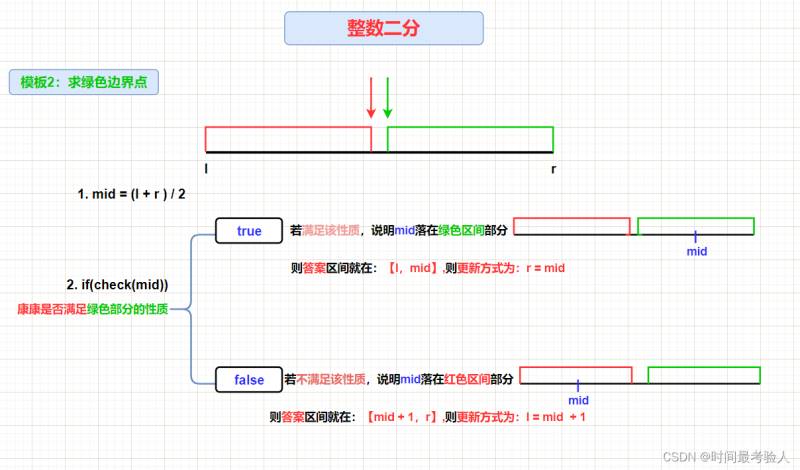
2.求解二分问题的思路

每次先划分区间，写一个mid，后面再考虑是否补上加1操作然后想一个check()函数，康康是否满足性质，根据check()函数的值取判断怎么划分(mid在哪一边)，到底是是l = mid，还是r = mid，第一种补上1即可。（关键是找性质，判断是否满足性质然后判断mid在左边还是右边）

3.练习

(1).数的范围

给定一个按照升序排列的长度为 nn 的整数数组，以及 qq 个查询。

对于每个查询，返回一个元素 kk 的起始位置和终止位置（位置从 00 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 nn 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q行，每行包含一个整数 k，表示一个询问元素。

输出格式

共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例：

6 31 2 2 3 3 4345

输出样例：

3 45 5-1 -1

思路：

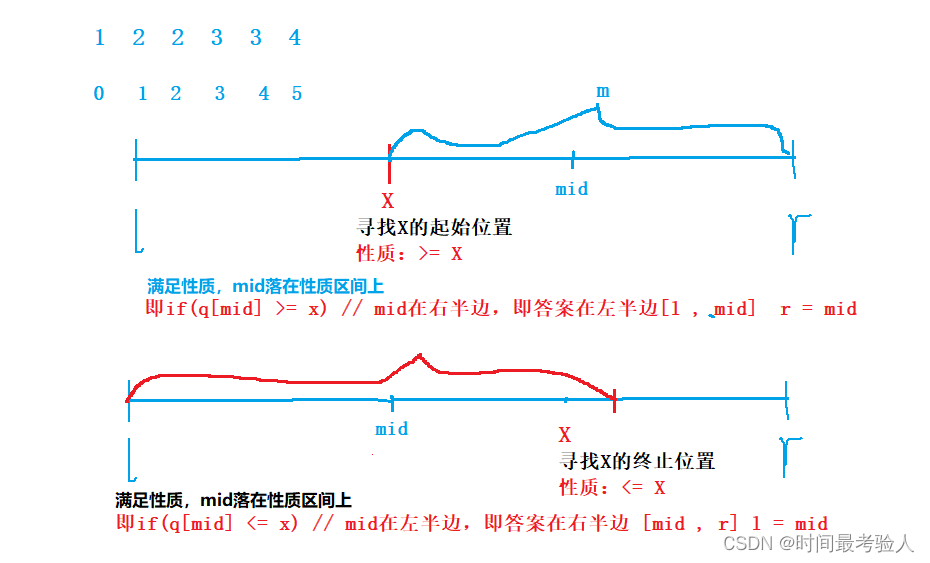
【参考代码】

#include<iostream>

using namespace std;
const int N = 100000+10;
int q[N];

int main()
{
    int n, m;
    cin>> n >> m;

    for(int i = 0; i < n; i++) cin>>q[i];
    while(m--)
    {
      int x;
      cin>> x;
      // 寻找起始位置
      int l = 0, r = n - 1;
      while(l < r)
      {
          int mid =(l + r)/2;
          if(q[mid] >= x) r = mid;
          else l = mid + 1;
      }
      if(q[l] != x) cout<<"-1 -1"<<endl;
      else{
          cout<<l<<" ";
          // 寻找终点位置
          int l = 0, r = n - 1;
          while(l<r)
          {
              int mid = (l + r + 1)/2;
              if(q[mid] <= x) l = mid;
              else r = mid - 1;
          }

          cout<< l << endl;
      }

    }
    return 0;
}

(2).0到n-1中缺失的数字

(二分) O(logn)
这道题目给定的是递增数组，假设数组中第一个缺失的数是 x，那么数组中的数如下所示；

从中可以看出，数组左边蓝色部分都满足nums[i] == i，数组右边橙色部分都不满足nums[i] == i，因此我们可以二分出分界点 x 的值。

另外要注意特殊情况：当所有数都满足nums[i] == i时，表示缺失的是 n。

时间复杂度分析
二分中的迭代只会执行 O(logn) 次，因此时间复杂度是O(logn)。

class Solution {
public:
    int getMissingNumber(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        int l = 0, r = nums.size() - 1;
        while(l < r)
        {
            int mid = (l + r)/2;
            if(nums[mid] != mid) r = mid; //在红色半边(满足条件)
            else l = mid + 1;
        }

        //缺的是n这个数
        if(nums[r] == r) r++;

        return r;

    }
};

二、浮点数二分

1.浮点数二分模板

浮点数二分算法模板 —— 模板题 AcWing 790. 数的三次方根
bool check(double x) {/* ... */} // 检查x是否满足某种性质（包含了计算和条件）

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求(一般比题目要求的大2)
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

注：与整数二分的最大区别是，else那里的条件l = mid不进行+1或者-1，浮点数没有整除（/ 下取整）这种问题，不需要处理边界。

2.练习

(1).数的三次方跟

给定一个浮点数 n，求它的三次方根。

输入格式

共一行，包含一个浮点数 n。

输出格式

共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围

−10000≤n≤10000

输入样例：

1000.00

输出样例：

10.000000

#include<iostream>

using namespace std;

int main()
{
    double n;
    cin>>n;

    double l = -10000, r = 10000;
     // eps 表示精度，取决于题目对精度的要求(保险1e-8)
    const double eps = 1e-8;
    while(r - l > eps)
    {
        double mid = (l + r) / 2;
        if(mid * mid * mid >= n) r = mid;
        else l = mid;
    }

     printf("%.6lf\n", l);
    return 0;

}

(2).一元三次方程求解

提示：记方程f(x)=0，若存在2个数x1和x2，且f(x1)*f(x2)<0，则在(x1,x2)之间一定有一个根。

#include<iostream>
#include<cstdio>

using namespace std;

double a, b, c, d;// 全局变量方便在cal中使用
const double eps = 1e-6;// 定义精度

//计算一元三次方程
double cal(double x)
{
    return a*x*x*x + b*x*x + c*x + d;
}
int main()
{
    cin>>a>>b>>c>>d;

    //枚举根
    for(int i = -100; i <= 100; i++)
    {
        //根与根之差的绝对值 ≥1
        double l = double(i), r = double(i + 1);// 细节:要将l,r转为double
        if(cal(l) == 0) printf("%.2lf ", l); //若f(x) = 0，根即为x 

        //f(x1)×f(x2) < 0 根在（x1,x2）之间—— 浮点二分
        else if(cal(l) * cal(r) < 0)
        {
            while(r - l > eps)
            {
                //x1 < x，f(x1)×f(x2)<0，则在(x1, x2)之间一定有一个根
                double mid = (l + r)/2;
                // check()条件
                if(cal(l) * cal(mid) <= 0) r = mid;
                else l = mid;
            }

            printf("%.2lf ", l);
        }
    }
}

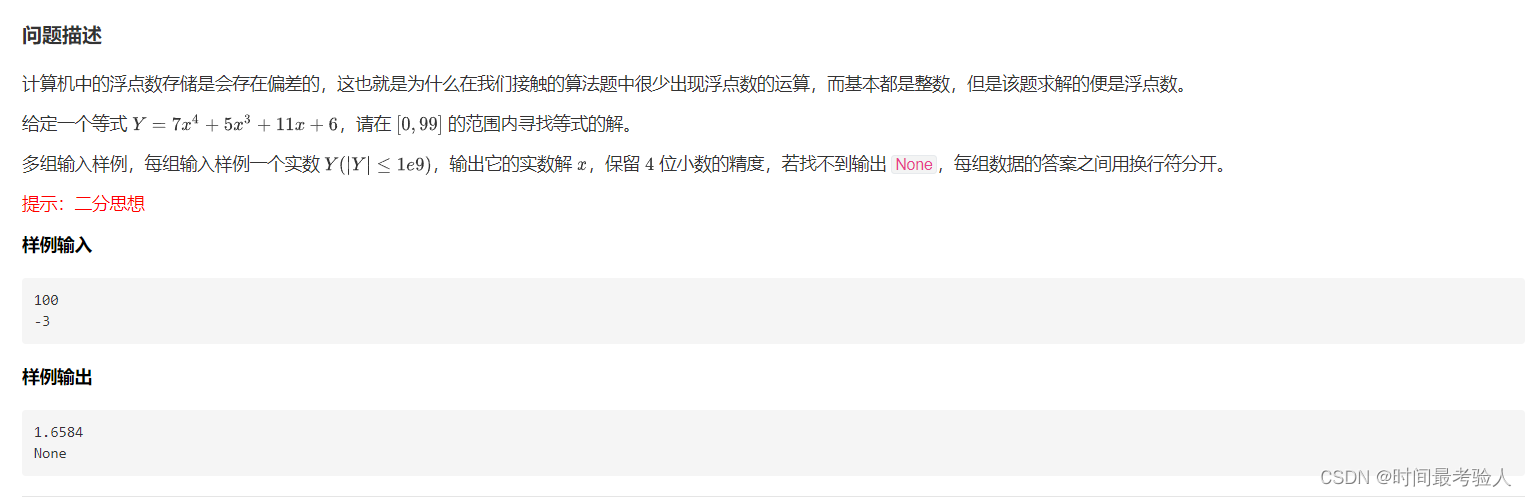
【参考代码】

#include <bits/stdc++.h>
using namespace std;

double check(double x)
{
    return 7*x*x*x*x + 5*x*x*x + 11*x + 6;
}
double erfen(double Y)
{
    double l=0.0, r=99.0, mid;
    while(r - l > 1e-6){
        mid = (l + r)/2;
        if(check(mid) > Y) r = mid;
        else l = mid;
    }
    return mid;
}
int main()
{
    double Y;
    while(~scanf("%lf", &Y)){
        if(Y < 6 || Y > 677269824)
            puts("None");
        else
        printf("%.4f\n", erfen(Y));
    }
    return 0;
}

三、总结

以上就是对基础二分知识和模板的再次回顾和总结，二分再掌握了基本原理之后，关键还是多练多总结，找到那种敏锐的体感，QAQ…，希望对你有所帮助呀！

到此这篇关于关于C++中二分法详解的文章就介绍到这了,更多相关C++二分法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！