用Python实现插值算法

数模比赛中，常常需要对数据进行处理和分析，但有时候数据不多，就需要一些方法“模拟产生”一些靠谱的值来满足需求，这就是插值的作用。本文不再具体介绍每个插值算法的内在原理，将直接通过调包实现。

下面，先上三件套，看一下原始数据的大致情况：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel('data.xlsx')

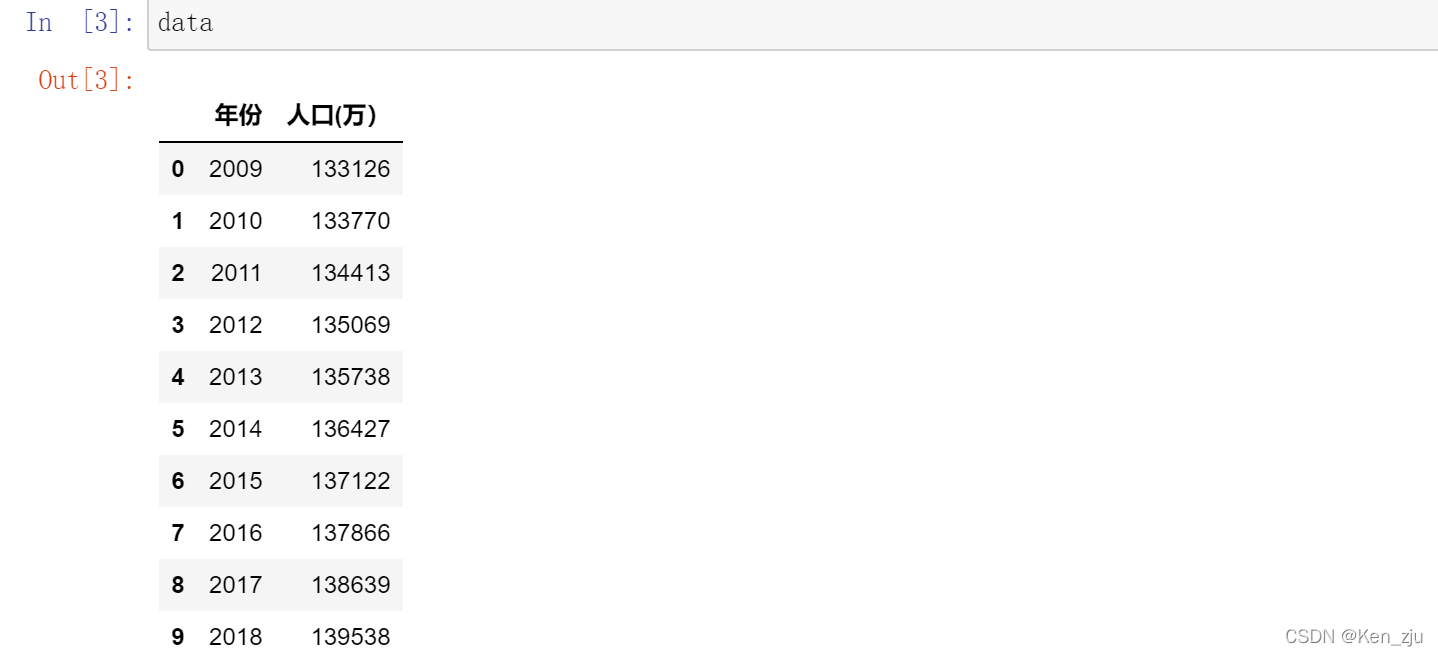
拉格朗日插值算法

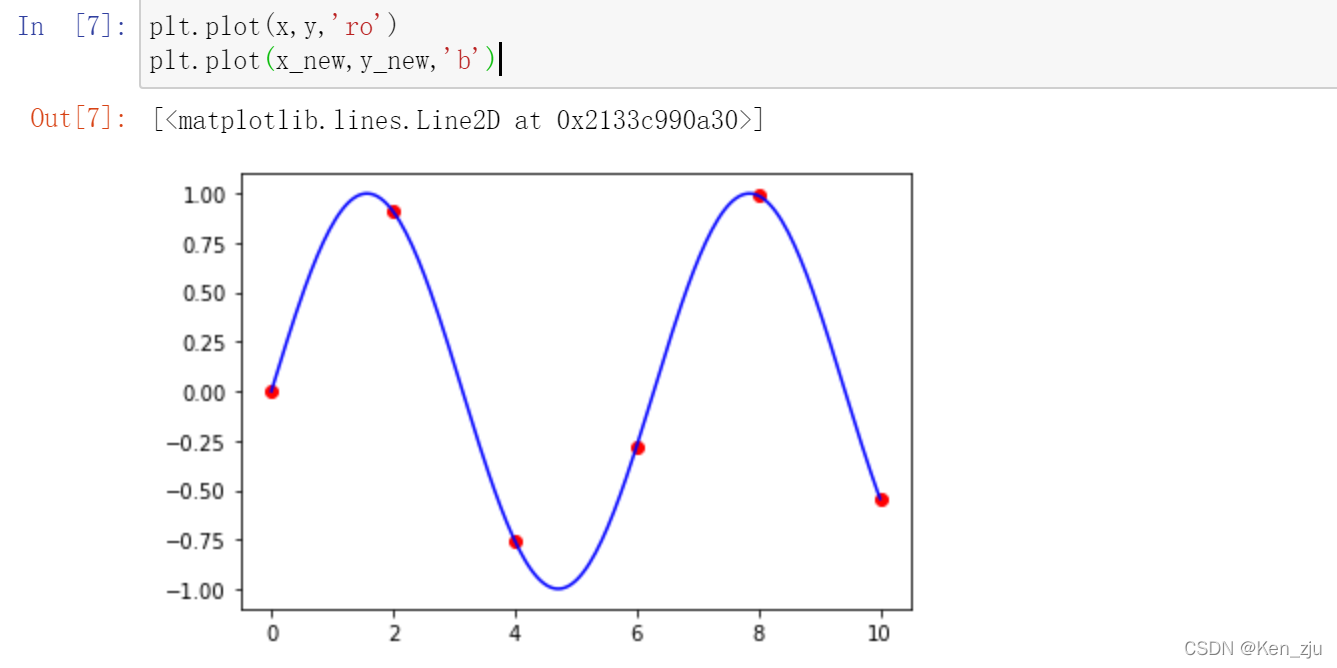
原始数据我们采用sin(x)的形式，看一下原始数据点：

import scipy
from scipy.interpolate import lagrange
x = np.linspace(0,10,6)      #0~10等差插入11个数，需要预测的值
y = np.sin(x)
x_new = np.linspace(0,10,200)  #用于绘制图形
y_new = np.sin(x_new)
plt.plot(x,y,'ro')
plt.plot(x_new,y_new,'b')

f1 = lagrange(x,y)
plt.plot(x,y,'ro')
plt.plot(x_new,y_new,'b')
plt.plot(x_new,f1(x_new),'g')

看一下拟合效果：

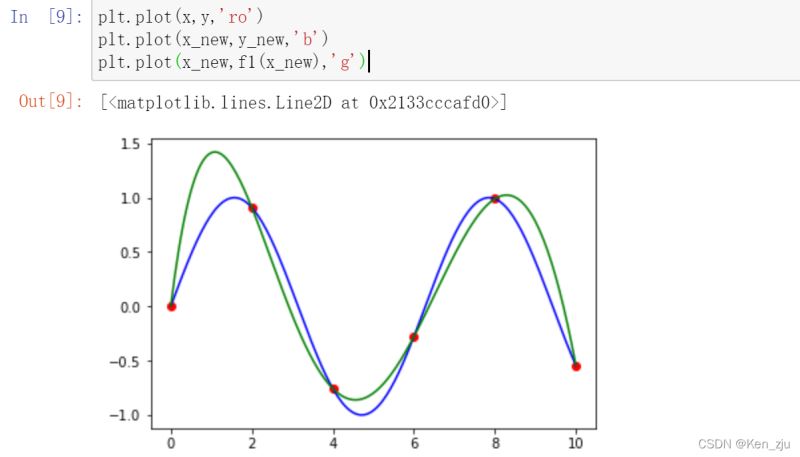
分段线性插值 

f4 = scipy.interpolate.interp1d(x,y,kind='linear')
plt.plot(x,y,'ro')
plt.plot(x_new,y_new,'b')
plt.plot(x_new,f4(x_new),'g')

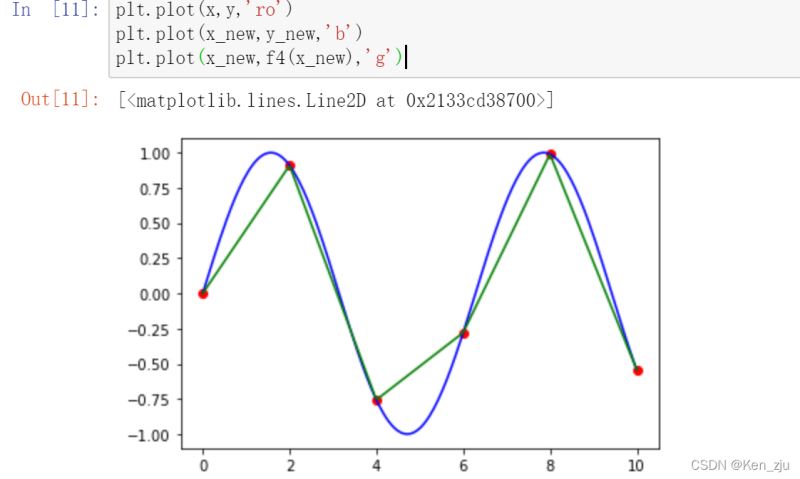
分段二次（三次）插值

f5 = scipy.interpolate.interp1d(x,y,kind='quadratic')    #三次就是cubic
plt.plot(x,y,'ro')
plt.plot(x_new,y_new,'b')
plt.plot(x_new,f5(x_new),'g')

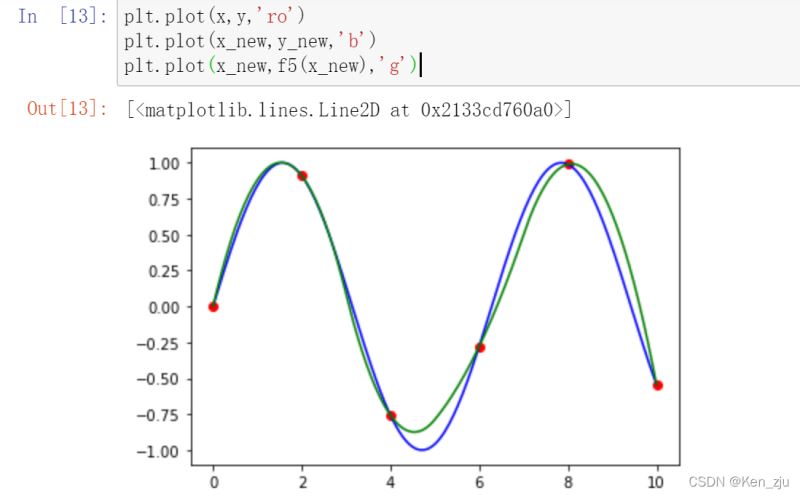
牛顿插值法：暂未找到相应的库

        分段三次埃尔米特插值

f5 = scipy.interpolate.interp1d(x,y,kind='quadratic')    #三次就是cubic
plt.plot(x,y,'ro')
plt.plot(x_new,y_new,'b')
plt.plot(x_new,f5(x_new),'g')

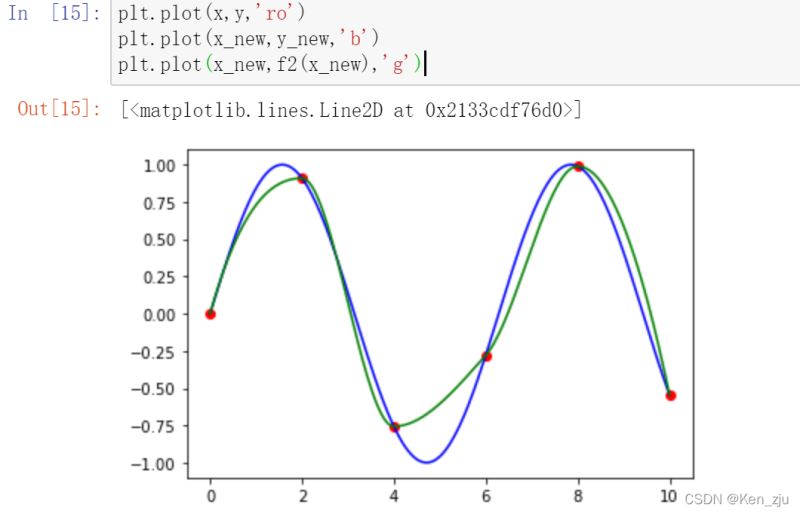
三次样条插值

f3 = scipy.interpolate.CubicSpline(x,y)
plt.plot(x,y,'ro')
plt.plot(x_new,y_new,'b')
plt.plot(x_new,f3(x_new),'g')

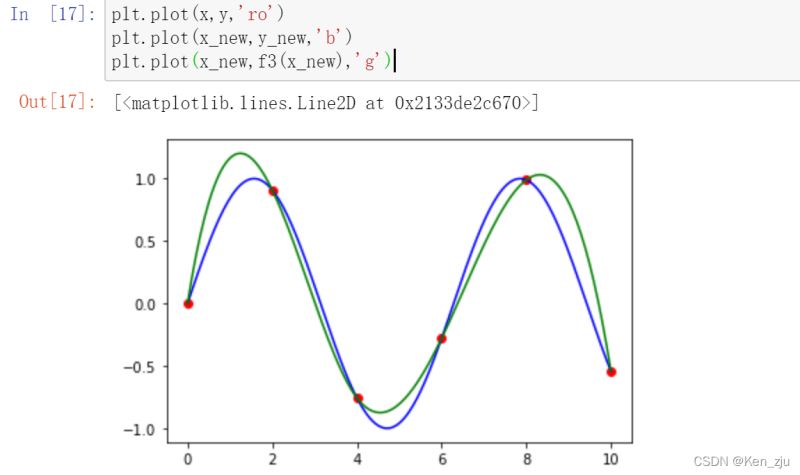
接下来，让我们看看一个具体实例的比较：

y = np.array(data)[:,1]
x = np.linspace(2009,2018,10)
x_new = np.array([2019,2020,2021])
f2 = scipy.interpolate.PchipInterpolator(x,y)
f3 = scipy.interpolate.CubicSpline(x,y)

#coding:utf-8
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

plt.plot(x,y,color='black',marker='o',label='样本点')
plt.plot(x_new,f2(x_new),'b-',marker='x',label='分段三次埃米尔特')
plt.plot(x_new,f3(x_new),'r-',marker='x',label='三次样条插值')
plt.xticks(range(2009,2022,1))     #调整x轴间距
plt.legend()
plt.show()

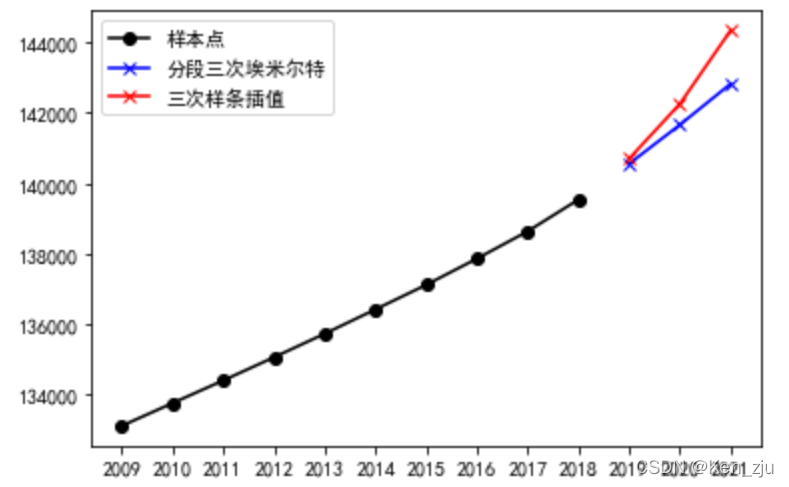
Tips：①最常用的就是埃尔米特三次插值、三次样条插值

②拉格朗日插值虽然在训练集上表现良好，但是在测试集上着实难堪，尤其拟合高阶函数时，千万不要轻易用此预测

到此这篇关于用Python实现插值算法的文章就介绍到这了,更多相关Python插值算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！