Python实现机器学习算法的分类

Python算法的分类

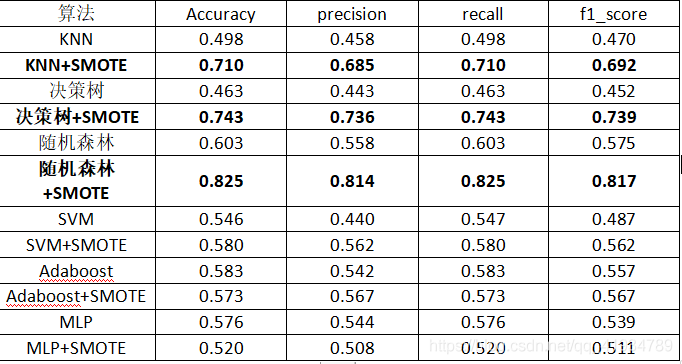
对葡萄酒数据集进行测试，由于数据集是多分类且数据的样本分布不平衡，所以直接对数据测试，效果不理想。所以使用SMOTE过采样对数据进行处理，对数据去重，去空，处理后数据达到均衡，然后进行测试，与之前测试相比，准确率提升较高。

例如：决策树：

Smote处理前：

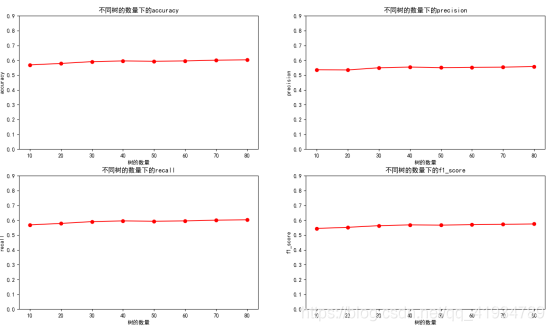
Smote处理后：

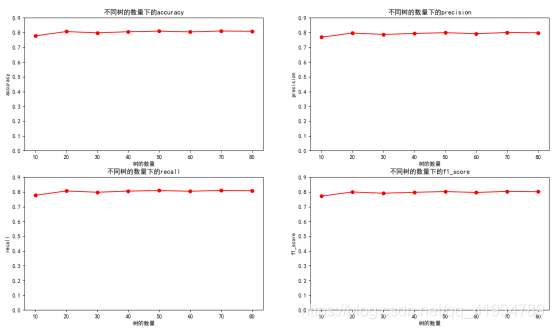
from typing import Counter
from matplotlib import colors, markers
import numpy as np
import pandas as pd
import operator
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.svm import SVC
# 判断模型预测准确率的模型
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_auc_score
from sklearn.metrics import f1_score
from sklearn.metrics import classification_report

#设置绘图内的文字
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

path ="C:\\Users\\zt\\Desktop\\winequality\\myexcel.xls"
# path=r"C:\\Users\\zt\\Desktop\\winequality\\winequality-red.csv"#您要读取的文件路径
# exceldata = np.loadtxt(
#     path,
#     dtype=str,
#     delimiter=";",#每列数据的隔开标志
#     skiprows=1
# )

# print(Counter(exceldata[:,-1]))

exceldata = pd.read_excel(path)
print(exceldata)

print(exceldata[exceldata.duplicated()])
print(exceldata.duplicated().sum())

#去重
exceldata = exceldata.drop_duplicates()

#判空去空
print(exceldata.isnull())
print(exceldata.isnull().sum)
print(exceldata[~exceldata.isnull()])
exceldata = exceldata[~exceldata.isnull()]

print(Counter(exceldata["quality"]))

#smote

#使用imlbearn库中上采样方法中的SMOTE接口
from imblearn.over_sampling import SMOTE
#定义SMOTE模型，random_state相当于随机数种子的作用

X,y = np.split(exceldata,(11,),axis=1)
smo = SMOTE(random_state=10) 

x_smo,y_smo = SMOTE().fit_resample(X.values,y.values)

print(Counter(y_smo))

x_smo = pd.DataFrame({"fixed acidity":x_smo[:,0], "volatile acidity":x_smo[:,1],"citric acid":x_smo[:,2] ,"residual sugar":x_smo[:,3] ,"chlorides":x_smo[:,4],"free sulfur dioxide":x_smo[:,5] ,"total sulfur dioxide":x_smo[:,6] ,"density":x_smo[:,7],"pH":x_smo[:,8] ,"sulphates":x_smo[:,9] ," alcohol":x_smo[:,10]})
y_smo = pd.DataFrame({"quality":y_smo})
print(x_smo.shape)
print(y_smo.shape)
#合并
exceldata = pd.concat([x_smo,y_smo],axis=1)
print(exceldata)

#分割X，y
X,y = np.split(exceldata,(11,),axis=1)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=10,train_size=0.7)
print("训练集大小：%d"%(X_train.shape[0]))
print("测试集大小：%d"%(X_test.shape[0]))

def func_mlp(X_train,X_test,y_train,y_test):
    print("神经网络MLP:")
    kk = [i for i in range(200,500,50) ] #迭代次数
    t_precision = []
    t_recall = []
    t_accuracy = []
    t_f1_score = []
    for n in kk:
        method = MLPClassifier(activation="tanh",solver='lbfgs', alpha=1e-5,
                    hidden_layer_sizes=(5, 2), random_state=1,max_iter=n)
        method.fit(X_train,y_train)
        MLPClassifier(activation='relu', alpha=1e-05, batch_size='auto', beta_1=0.9,
                        beta_2=0.999, early_stopping=False, epsilon=1e-08,
                        hidden_layer_sizes=(5, 2), learning_rate='constant',
                        learning_rate_init=0.001, max_iter=n, momentum=0.9,
                        nesterovs_momentum=True, power_t=0.5, random_state=1, shuffle=True,
                        solver='lbfgs', tol=0.0001, validation_fraction=0.1, verbose=False,
                        warm_start=False)
        y_predict = method.predict(X_test)
        t =classification_report(y_test, y_predict, target_names=['3','4','5','6','7','8'],output_dict=True)
        print(t)
        t_accuracy.append(t["accuracy"])
        t_precision.append(t["weighted avg"]["precision"])
        t_recall.append(t["weighted avg"]["recall"])
        t_f1_score.append(t["weighted avg"]["f1-score"])
    plt.figure("数据未处理MLP")
    plt.subplot(2,2,1)
    #添加文本 #x轴文本
    plt.xlabel('迭代次数')
    #y轴文本
    plt.ylabel('accuracy')
    #标题
    plt.title('不同迭代次数下的accuracy')
    plt.plot(kk,t_accuracy,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,2)
    #添加文本 #x轴文本
    plt.xlabel('迭代次数')
    #y轴文本
    plt.ylabel('precision')
    #标题
    plt.title('不同迭代次数下的precision')
    plt.plot(kk,t_precision,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,3)
    #添加文本 #x轴文本
    plt.xlabel('迭代次数')
    #y轴文本
    plt.ylabel('recall')
    #标题
    plt.title('不同迭代次数下的recall')
    plt.plot(kk,t_recall,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,4)
    #添加文本 #x轴文本
    plt.xlabel('迭代次数')
    #y轴文本
    plt.ylabel('f1_score')
    #标题
    plt.title('不同迭代次数下的f1_score')
    plt.plot(kk,t_f1_score,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.show()

def func_svc(X_train,X_test,y_train,y_test):
    print("向量机：")
    kk = ["linear","poly","rbf"] #核函数类型
    t_precision = []
    t_recall = []
    t_accuracy = []
    t_f1_score = []
    for n in kk:
        method = SVC(kernel=n, random_state=0)
        method = method.fit(X_train, y_train)
        y_predic = method.predict(X_test)
        t =classification_report(y_test, y_predic, target_names=['3','4','5','6','7','8'],output_dict=True)
        print(t)
        t_accuracy.append(t["accuracy"])
        t_precision.append(t["weighted avg"]["precision"])
        t_recall.append(t["weighted avg"]["recall"])
        t_f1_score.append(t["weighted avg"]["f1-score"])
    plt.figure("数据未处理向量机")
    plt.subplot(2,2,1)
    #添加文本 #x轴文本
    plt.xlabel('核函数类型')
    #y轴文本
    plt.ylabel('accuracy')
    #标题
    plt.title('不同核函数类型下的accuracy')
    plt.plot(kk,t_accuracy,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,2)
    #添加文本 #x轴文本
    plt.xlabel('核函数类型')
    #y轴文本
    plt.ylabel('precision')
    #标题
    plt.title('不同核函数类型下的precision')
    plt.plot(kk,t_precision,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,3)
    #添加文本 #x轴文本
    plt.xlabel('核函数类型')
    #y轴文本
    plt.ylabel('recall')
    #标题
    plt.title('不同核函数类型下的recall')
    plt.plot(kk,t_recall,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,4)
    #添加文本 #x轴文本
    plt.xlabel('核函数类型')
    #y轴文本
    plt.ylabel('f1_score')
    #标题
    plt.title('不同核函数类型下的f1_score')
    plt.plot(kk,t_f1_score,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.show()

def func_classtree(X_train,X_test,y_train,y_test):
    print("决策树：")
    kk = [10,20,30,40,50,60,70,80,90,100] #决策树最大深度
    t_precision = []
    t_recall = []
    t_accuracy = []
    t_f1_score = []
    for n in kk:
        method = tree.DecisionTreeClassifier(criterion="gini",max_depth=n)
        method.fit(X_train,y_train)
        predic = method.predict(X_test)
        print("method.predict:%f"%method.score(X_test,y_test))

        t =classification_report(y_test, predic, target_names=['3','4','5','6','7','8'],output_dict=True)
        print(t)
        t_accuracy.append(t["accuracy"])
        t_precision.append(t["weighted avg"]["precision"])
        t_recall.append(t["weighted avg"]["recall"])
        t_f1_score.append(t["weighted avg"]["f1-score"])
    plt.figure("数据未处理决策树")
    plt.subplot(2,2,1)
    #添加文本 #x轴文本
    plt.xlabel('决策树最大深度')
    #y轴文本
    plt.ylabel('accuracy')
    #标题
    plt.title('不同决策树最大深度下的accuracy')
    plt.plot(kk,t_accuracy,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,2)
    #添加文本 #x轴文本
    plt.xlabel('决策树最大深度')
    #y轴文本
    plt.ylabel('precision')
    #标题
    plt.title('不同决策树最大深度下的precision')
    plt.plot(kk,t_precision,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,3)
    #添加文本 #x轴文本
    plt.xlabel('决策树最大深度')
    #y轴文本
    plt.ylabel('recall')
    #标题
    plt.title('不同决策树最大深度下的recall')
    plt.plot(kk,t_recall,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,4)
    #添加文本 #x轴文本
    plt.xlabel('决策树最大深度')
    #y轴文本
    plt.ylabel('f1_score')
    #标题
    plt.title('不同决策树最大深度下的f1_score')
    plt.plot(kk,t_f1_score,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.show()

def func_adaboost(X_train,X_test,y_train,y_test):
    print("提升树：")
    kk = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8]
    t_precision = []
    t_recall = []
    t_accuracy = []
    t_f1_score = []
    for n in range(100,200,200):
        for k in kk:
            print("迭代次数为：%d\n学习率：%.2f"%(n,k))
            bdt = AdaBoostClassifier(tree.DecisionTreeClassifier(max_depth=2, min_samples_split=20),
                                    algorithm="SAMME",
                                    n_estimators=n, learning_rate=k)
            bdt.fit(X_train, y_train)
            #迭代100次 ,学习率为0.1
            y_pred = bdt.predict(X_test)
            print("训练集score：%lf"%(bdt.score(X_train,y_train)))
            print("测试集score：%lf"%(bdt.score(X_test,y_test)))
            print(bdt.feature_importances_)

            t =classification_report(y_test, y_pred, target_names=['3','4','5','6','7','8'],output_dict=True)
            print(t)
            t_accuracy.append(t["accuracy"])
            t_precision.append(t["weighted avg"]["precision"])
            t_recall.append(t["weighted avg"]["recall"])
            t_f1_score.append(t["weighted avg"]["f1-score"])
    plt.figure("数据未处理迭代100次(adaboost)")
    plt.subplot(2,2,1)
    #添加文本 #x轴文本
    plt.xlabel('学习率')
    #y轴文本
    plt.ylabel('accuracy')
    #标题
    plt.title('不同学习率下的accuracy')
    plt.plot(kk,t_accuracy,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,2)
    #添加文本 #x轴文本
    plt.xlabel('学习率')
    #y轴文本
    plt.ylabel('precision')
    #标题
    plt.title('不同学习率下的precision')
    plt.plot(kk,t_precision,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,3)
    #添加文本 #x轴文本
    plt.xlabel('学习率')
    #y轴文本
    plt.ylabel('recall')
    #标题
    plt.title('不同学习率下的recall')
    plt.plot(kk,t_recall,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,4)
    #添加文本 #x轴文本
    plt.xlabel('学习率')
    #y轴文本
    plt.ylabel('f1_score')
    #标题
    plt.title('不同学习率下的f1_score')
    plt.plot(kk,t_f1_score,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.show()

# inX 用于分类的输入向量
# dataSet表示训练样本集
# 标签向量为labels，标签向量的元素数目和矩阵dataSet的行数相同
# 参数k表示选择最近邻居的数目
def classify0(inx, data_set, labels, k):
    """实现k近邻"""
    data_set_size = data_set.shape[0]   # 数据集个数，即行数
    diff_mat = np.tile(inx, (data_set_size, 1)) - data_set   # 各个属性特征做差
    sq_diff_mat = diff_mat**2  # 各个差值求平方
    sq_distances = sq_diff_mat.sum(axis=1)  # 按行求和
    distances = sq_distances**0.5   # 开方
    sorted_dist_indicies = distances.argsort()  # 按照从小到大排序，并输出相应的索引值
    class_count = {}  # 创建一个字典，存储k个距离中的不同标签的数量

    for i in range(k):
        vote_label = labels[sorted_dist_indicies[i]]  # 求出第i个标签

        # 访问字典中值为vote_label标签的数值再加1，
        #class_count.get(vote_label, 0)中的0表示当为查询到vote_label时的默认值
        class_count[vote_label[0]] = class_count.get(vote_label[0], 0) + 1
    # 将获取的k个近邻的标签类进行排序
    sorted_class_count = sorted(class_count.items(),
    key=operator.itemgetter(1), reverse=True)
    # 标签类最多的就是未知数据的类
    return sorted_class_count[0][0]

def func_knn(X_train,X_test,y_train,y_test):
    print("k近邻：")
    kk = [i for i in range(3,30,5)] #k的取值
    t_precision = []
    t_recall = []
    t_accuracy = []
    t_f1_score = []
    for n in kk:
        y_predict = []
        for x in X_test.values:
            a = classify0(x, X_train.values, y_train.values, n)  # 调用k近邻分类
            y_predict.append(a)

        t =classification_report(y_test, y_predict, target_names=['3','4','5','6','7','8'],output_dict=True)
        print(t)
        t_accuracy.append(t["accuracy"])
        t_precision.append(t["weighted avg"]["precision"])
        t_recall.append(t["weighted avg"]["recall"])
        t_f1_score.append(t["weighted avg"]["f1-score"])
    plt.figure("数据未处理k近邻")
    plt.subplot(2,2,1)
    #添加文本 #x轴文本
    plt.xlabel('k值')
    #y轴文本
    plt.ylabel('accuracy')
    #标题
    plt.title('不同k值下的accuracy')
    plt.plot(kk,t_accuracy,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,2)
    #添加文本 #x轴文本
    plt.xlabel('k值')
    #y轴文本
    plt.ylabel('precision')
    #标题
    plt.title('不同k值下的precision')
    plt.plot(kk,t_precision,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,3)
    #添加文本 #x轴文本
    plt.xlabel('k值')
    #y轴文本
    plt.ylabel('recall')
    #标题
    plt.title('不同k值下的recall')
    plt.plot(kk,t_recall,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,4)
    #添加文本 #x轴文本
    plt.xlabel('k值')
    #y轴文本
    plt.ylabel('f1_score')
    #标题
    plt.title('不同k值下的f1_score')
    plt.plot(kk,t_f1_score,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.show()

def func_randomforest(X_train,X_test,y_train,y_test):
    print("随机森林：")
    t_precision = []
    t_recall = []
    t_accuracy = []
    t_f1_score = []
    kk = [10,20,30,40,50,60,70,80] #默认树的数量
    for n in kk:
        clf = RandomForestClassifier(n_estimators=n, max_depth=100,min_samples_split=2, random_state=10,verbose=True)
        clf.fit(X_train,y_train)
        predic = clf.predict(X_test)

        print("特征重要性：",clf.feature_importances_)
        print("acc:",clf.score(X_test,y_test))

        t =classification_report(y_test, predic, target_names=['3','4','5','6','7','8'],output_dict=True)
        print(t)
        t_accuracy.append(t["accuracy"])
        t_precision.append(t["weighted avg"]["precision"])
        t_recall.append(t["weighted avg"]["recall"])
        t_f1_score.append(t["weighted avg"]["f1-score"])
    plt.figure("数据未处理深度100（随机森林）")
    plt.subplot(2,2,1)
    #添加文本 #x轴文本
    plt.xlabel('树的数量')
    #y轴文本
    plt.ylabel('accuracy')
    #标题
    plt.title('不同树的数量下的accuracy')
    plt.plot(kk,t_accuracy,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,2)
    #添加文本 #x轴文本
    plt.xlabel('树的数量')
    #y轴文本
    plt.ylabel('precision')
    #标题
    plt.title('不同树的数量下的precision')
    plt.plot(kk,t_precision,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,3)
    #添加文本 #x轴文本
    plt.xlabel('树的数量')
    #y轴文本
    plt.ylabel('recall')
    #标题
    plt.title('不同树的数量下的recall')
    plt.plot(kk,t_recall,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.subplot(2,2,4)
    #添加文本 #x轴文本
    plt.xlabel('树的数量')
    #y轴文本
    plt.ylabel('f1_score')
    #标题
    plt.title('不同树的数量下的f1_score')
    plt.plot(kk,t_f1_score,color="r",marker="o",lineStyle="-")
    plt.yticks(np.arange(0,1,0.1))

    plt.show()

if __name__ == '__main__':
    #神经网络
    print(func_mlp(X_train,X_test,y_train,y_test))
    #向量机
    print(func_svc(X_train,X_test,y_train,y_test))
    #决策树
    print(func_classtree(X_train,X_test,y_train,y_test))
    #提升树
    print(func_adaboost(X_train,X_test,y_train,y_test))
    #knn
    print(func_knn(X_train,X_test,y_train,y_test))
    #randomforest
    print(func_randomforest(X_train,X_test,y_train,y_test))

到此这篇关于Python实现机器学习算法的分类的文章就介绍到这了,更多相关Python算法分类内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！