python二叉树类以及其4种遍历方法实例

目录

• 前言
• 实例代码：
• 相关阅读内容：
• 总结

前言

之前学习过binarytree第三方库，了解了它定义的各种基本用法。

昨天在问答频道中做题时碰到一个关于二叉树的算法填空题，感觉代码不错非常值得学习，于是整理代码分享如下：

实例代码：

from collections import deque  #层遍历中用到队列数据类型

class BTNode:   #二叉链中结点类
    def __init__(self,d = None):
        self.data = d       #结点值
        self.lchild = None  #左hai子指针
        self.rchild = None  #右hai子指针

class BTree: #二叉树类
    def __init__(self,d = None):
        self.b = None       #根结点指针

    def DispBTree(self):    #返回二叉链的括号表示串
        return self._DispBTree1(self.b)

    def _DispBTree1(self,t):    #被DispBTree方法调用
        if t==None:             #空树返回空串
            return ""
        else:
            bstr = t.data       #输出根结点值
            if t.lchild != None or t.rchild != None:
                bstr += "("     #有hai子结点时输出"("
                bstr += self._DispBTree1(t.lchild)    #递归输出左子树
            if t.rchild != None:
                bstr += ","     #有右hai子结点时输出","
                bstr += self._DispBTree1(t.rchild)    #递归输出右子树
                bstr += ")"     #输出")"
        return bstr

    def FindNode(self,x):       #查找值为x的结点算法
        return self._FindNode1(self.b,x)

    def _FindNode1(self,t,x):   #被FindNode方法调用
        if t==None:
            return None         #t为空时返回null
        elif t.data==x:
            return t            #t所指结点值为x时返回t
        else:
            p = self._FindNode1(t.lchild,x)    #在左子树中查找
        if p != None:
            return p            #在左子树中找到p结点，返回p
        else:
            return self._FindNode1(t.rchild,x)  #返回在右子树中查找结果

    def Height(self):           #求二叉树高度的算法
        return self._Height1(self.b)

    def _Height1(self,t):       #被Height方法调用
        if t==None:
            return 0            #空树的高度为0
        else:
            lh = self._Height1(t.lchild)    #求左子树高度lchildh
            rh = self._Height1(t.rchild)    #求右子树高度rchildh
        return max(lh,rh)+1

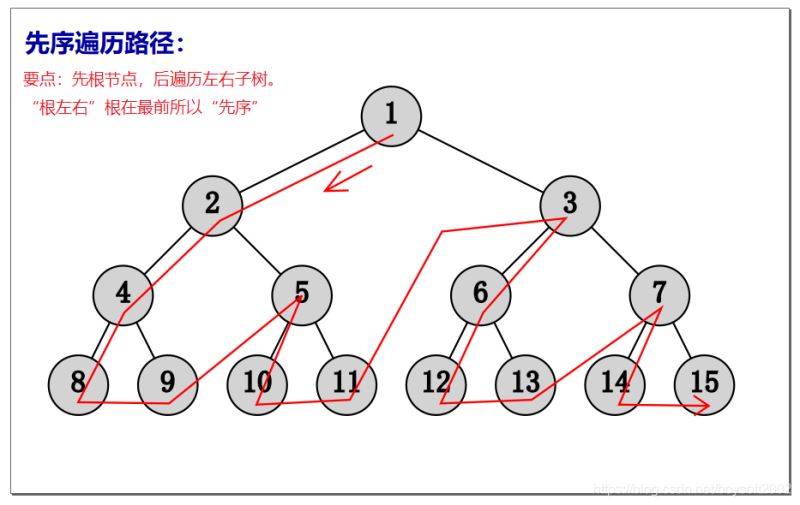
def PreOrder(bt):   #先序遍历的递归算法
    _PreOrder(bt.b)

def _PreOrder(t):   #被PreOrder方法调用
    if t != None:
        print(t.data,end = ' ')     #访问根结点
        _PreOrder(t.lchild)         #先序遍历左子树
        _PreOrder(t.rchild)         #先序遍历右子树

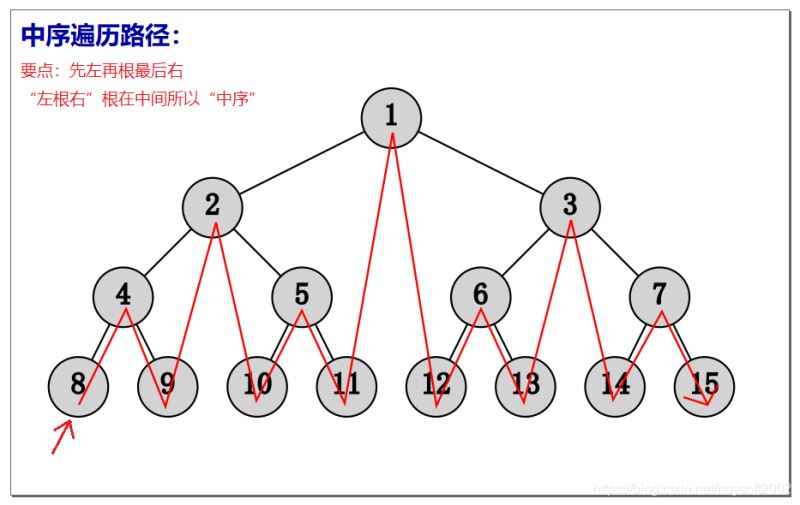
def InOrder(bt):    #中序遍历的递归算法
    _InOrder(bt.b)

def _InOrder(t):    #被InOrder方法调用
    if t != None:
        _InOrder(t.lchild)          #中序遍历左子树
        print(t.data,end = ' ')     #访问根结点
        _InOrder(t.rchild)          #中序遍历右子树

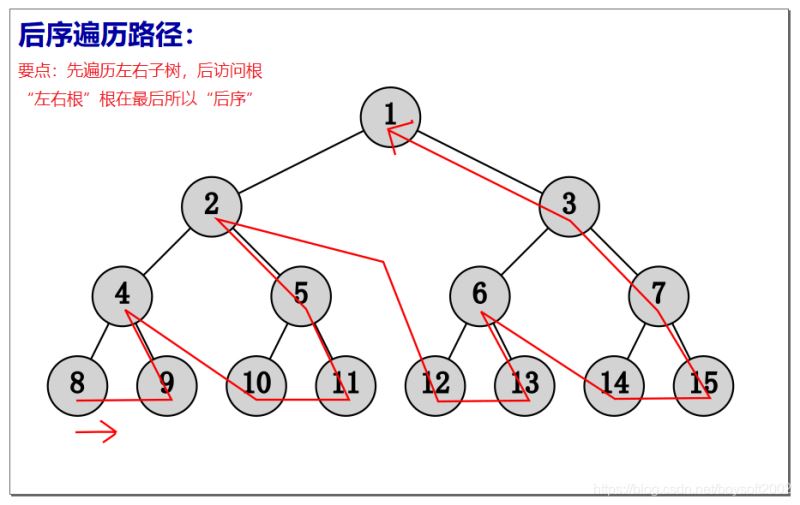
def PostOrder(bt):  #后序遍历的递归算法
    _PostOrder(bt.b)

def _PostOrder(t):  #被PostOrder方法调用
    if t != None:
        _PostOrder(t.lchild)        #后序遍历左子树
        _PostOrder(t.rchild)        #后序遍历右子树
        print(t.data,end = ' ')     #访问根结点

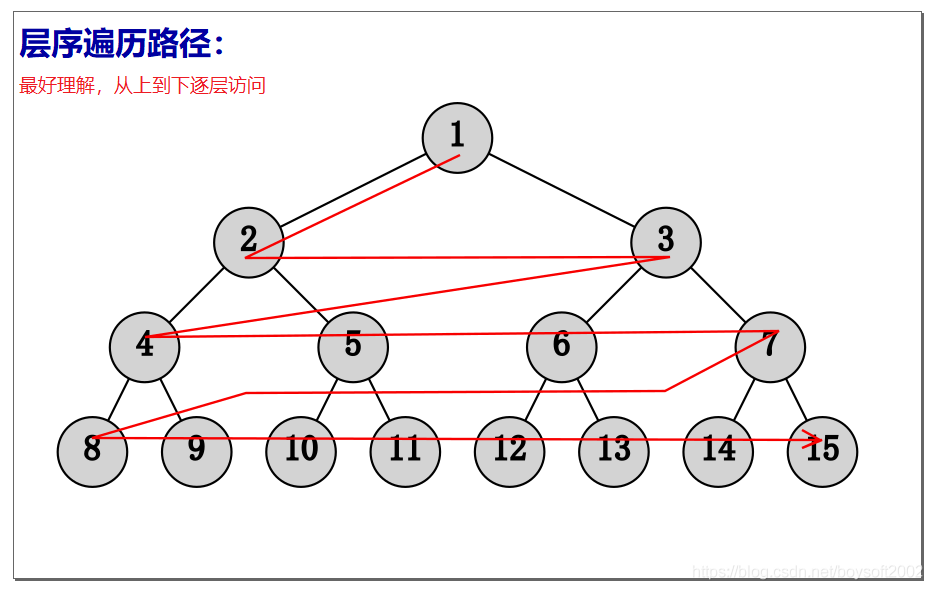
def LevelOrder(bt): #层序遍历的算法
    qu = deque()            #将双端队列作为普通队列qu
    qu.append(bt.b)         #根结点进队
    while len(qu)>0:        #队不空循环
        p = qu.popleft()            #出队一个结点
        print(p.data,end = ' ')     #访问p结点
        if p.lchild != None:        #有左hai子时将其进队
            qu.append(p.lchild)
        if p.rchild != None:        #有右hai子时将其进队
            qu.append(p.rchild)

def CreateBTree2(posts,ins):        #由后序序列posts和中序序列ins构造二叉链
    bt = BTree()
    bt.b = _CreateBTree2(posts,0,ins,0,len(posts))
    return bt

def _CreateBTree2(posts,i,ins,j,n):
    if n <= 0:
        return None
    d = posts[i+n-1]        #取后序序列尾元素d
    t = BTNode(d)           #创建根结点(结点值为d)
    p = ins.index(d)        #在ins中找到根结点的索引
    k = p-j                 #确定左子树中结点个数k
    t.lchild = _CreateBTree2(posts,i,ins,j,k)           #递归构造左子树
    t.rchild = _CreateBTree2(posts,i+k,ins,p+1,n-k-1)   #递归构造右子树
    return t

if __name__ == '__main__':

    inlst = ['D','G','B','A','E','C','F']
    posts = ['G','D','B','E','F','C','A']

    print(f"中序列表 ：{inlst}")
    print(f"后序列表 ：{posts}")

    #构造二叉树bt
    bt = BTree()
    bt = CreateBTree2(posts,inlst)
    print(f"\n构造二叉树：{bt.DispBTree()}")

    x = 'F'
    if bt.FindNode(x):
        print(f"bt中存在 ：'{x}'")
    else:
        print(f"bt中不存在 ：'{x}'")

    print(f"bt的高度 ：{bt.Height():^3}")

    print("\n先序遍历 ：",end='')
    PreOrder(bt)
    print("\n中序遍历列 ：",end='')
    InOrder(bt)
    print("\n后序遍历 ：",end='')
    PostOrder(bt)
    print("\n层序遍历 ：",end='')
    LevelOrder(bt)

中序列表：['D', 'G', 'B', 'A', 'E', 'C', 'F']
后序列表：['G', 'D', 'B', 'E', 'F', 'C', 'A']

构造二叉树：A(B(D(,G),C(E,F))
bt中存在 ：'F'
bt的高度 ： 4

先序遍历 ：A B D G C E F 
中序遍历 ：D G B A E C F 
后序遍历 ：G D B E F C A 
层序遍历 ：A B C D E F G

相关阅读内容：

• Python 初识二叉树，新手也秒懂！
• Python 初识二叉树，新手也秒懂！（续：实战binarytree）

总结

到此这篇关于python二叉树类以及其4种遍历方法的文章就介绍到这了,更多相关python二叉树类遍历内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！