C++实现LeetCode(51.N皇后问题)

[LeetCode] 51. N-Queens N皇后问题

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

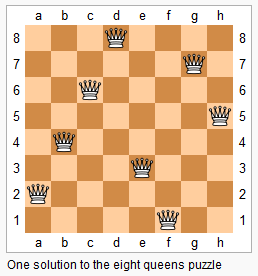
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

Input: 4
Output: [
[".Q..",  // Solution 1
"...Q",
"Q...",
"..Q."],

["..Q.",  // Solution 2
"Q...",
"...Q",
".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

经典的N皇后问题，基本所有的算法书中都会包含的问题。可能有些人对国际象棋不太熟悉，大家都知道中国象棋中最叼的是车，横竖都能走，但是在国际象棋中还有更叼的，就是皇后，不但能横竖走，还能走两个斜线，有如 bug 一般的存在。所以经典的八皇后问题就应运而生了，在一个 8x8 大小的棋盘上如果才能放8个皇后，使得两两之间不能相遇，所谓一山不能容二虎，而这里有八个母老虎，互相都不能相遇。对于这类问题，没有太简便的方法，只能使用穷举法，就是尝试所有的组合，每放置一个新的皇后的时候，必须要保证跟之前的所有皇后不能冲突，若发生了冲突，说明当前位置不能放，要重新找地方，这个逻辑非常适合用递归来做。我们先建立一个长度为 nxn 的全是点的数组 queens，然后从第0行开始调用递归。在递归函数中，我们首先判断当前行数是否已经为n，是的话，说明所有的皇后都已经成功放置好了，所以我们只要将 queens 数组加入结果 res 中即可。否则的话，我们遍历该行的所有列的位置，行跟列的位置都确定后，我们要验证当前位置是否会产生冲突，那么就需要使用一个子函数来判断了，首先验证该列是否有冲突，就遍历之前的所有行，若某一行相同列也有皇后，则冲突返回false；再验证两个对角线是否冲突，就是一些坐标转换，主要不要写错了，若都没有冲突，则说明该位置可以放皇后，放了新皇后之后，再对下一行调用递归即可，注意递归结束之后要返回状态，参见代码如下：

解法一：

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> res;
        vector<string> queens(n, string(n, '.'));
        helper(0, queens, res);
        return res;
    }
    void helper(int curRow, vector<string>& queens, vector<vector<string>>& res) {
        int n = queens.size();
        if (curRow == n) {
            res.push_back(queens);
            return;
        }
        for (int i = 0; i < n; ++i) {
            if (isValid(queens, curRow, i)) {
                queens[curRow][i] = 'Q';
                helper(curRow + 1, queens, res);
                queens[curRow][i] = '.';
            }
        }
    }
    bool isValid(vector<string>& queens, int row, int col) {
        for (int i = 0; i < row; ++i) {
            if (queens[i][col] == 'Q') return false;
        }
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; --i, --j) {
            if (queens[i][j] == 'Q') return false;
        }
        for (int i = row - 1, j = col + 1; i >= 0 && j < queens.size(); --i, ++j) {
            if (queens[i][j] == 'Q') return false;
        }
        return true;
    }
};

我们还可以只使用一个一维数组 queenCol 来保存所有皇后的列位置，初始化均为-1， 那么 queenCol[i] 就是表示第i个皇后在 (i, queenCol[i]) 位置，递归函数还是跟上面的解法相同，就是在当前行数等于n的时候，我们要将 queenCol 还原成一个 nxn 大小的矩阵，并存入结果 res 中。这种记录每个皇后的坐标的方法在验证冲突的时候比较简单，只要从第0行遍历到当前行，若跟之前的皇后的列数相同，直接返回false，叼就叼在判断对角线冲突非常简便，因为当两个点在同一条对角线上，那么二者的横坐标差的绝对值等于纵坐标差的绝对值，利用这条性质，可以快速的判断冲突，代码如下：

解法二：

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> res;
        vector<int> queenCol(n, -1);
        helper(0, queenCol, res);
        return res;
    }
    void helper(int curRow, vector<int>& queenCol, vector<vector<string>>& res) {
        int n = queenCol.size();
        if (curRow == n) {
            vector<string> out(n, string(n, '.'));
            for (int i = 0; i < n; ++i) {
                out[i][queenCol[i]] = 'Q';
            }
            res.push_back(out);
            return;
        }
        for (int i = 0; i < n; ++i) {
            if (isValid(queenCol, curRow, i)) {
                queenCol[curRow] = i;
                helper(curRow + 1, queenCol, res);
                queenCol[curRow] = -1;
            }
        }
    }
    bool isValid(vector<int>& queenCol, int row, int col) {
        for (int i = 0; i < row; ++i) {
            if (col == queenCol[i] || abs(row - i) == abs(col - queenCol[i])) return false;
        }
        return true;
    }
};

到此这篇关于C++实现LeetCode(51.N皇后问题)的文章就介绍到这了,更多相关C++实现N皇后问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！