C++高级数据结构之线段树

目录

• 前言：
• 高级数据结构（Ⅲ）线段树（Segment Tree）
• 线段树的原理
• 树的创建
• 单点修改
• 区间查找
• 完整代码及测试

前言：

• 高级数据结构（Ⅲ）线段树（Segment Tree）
• 线段树的原理
• 树的创建
• 单点修改
• 区间查找
• 完整代码及测试

高级数据结构（Ⅲ）线段树（Segment Tree）

线段树的原理

线段树是一种二叉搜索树 ， 对于线段树中的每一个非叶子结点[a,b]，它的左儿子表示的区间为[a, (a+b)/2]，右儿子表示的区间为[(a+b)/2+1, b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度，其空间复杂度为O(n)。

若对于一个数组使用前缀和数组保存它的区间和，那么查找区间和时间复杂度为O(1)，而区间修改时间复杂度为O(n)。使用线段树可以快速查找或修改某个区间的值，时间复杂度为O(logN)。

线段树中每一个结点代表一个区间，对于区间【1， 7】线段树的结构如下图

实例：

class SegmentTree{
private static final int[] tree = new int[1000];
int[] arr;
SegmentTree() {
}
SegmentTree(int[] arr) {
this.arr = arr;
}
//创建树···
public void buildTree(){}
//单点修改更新树
public void updateTree(){}
//区间查找
public void queryTree(){}
}

树的创建

给定一个数组arr = [6, 4, 7, 5, 8, 3 , 9]，创建它对应的线段树数组。

对于一个结点k，它的左孩子为2 * k，右孩子为 2 * k + 1，此公式适用于根结点从1开始。但我们在数组中存储元素时下标通常是从0开始的，即根结点从0开始，此时它的左孩子为 2 * k + 1， 右孩子为 2 * k + 2。

如下图所示，数组arr的长度为7，由于树是以2为基数的，且线段树中叶子结点保存的是arr中单个结点的值，我们可以将数组arr的长度设想为8 （2 ^ 3 = 8，理解为新添了一个元素0，这对区间和并不影响），此时它对应的线段树就是一棵结点数为15（1 + 2 + 4 + 8）的满二叉树。相应的结点值，映射到数组tree的值在图中可清晰的看出。

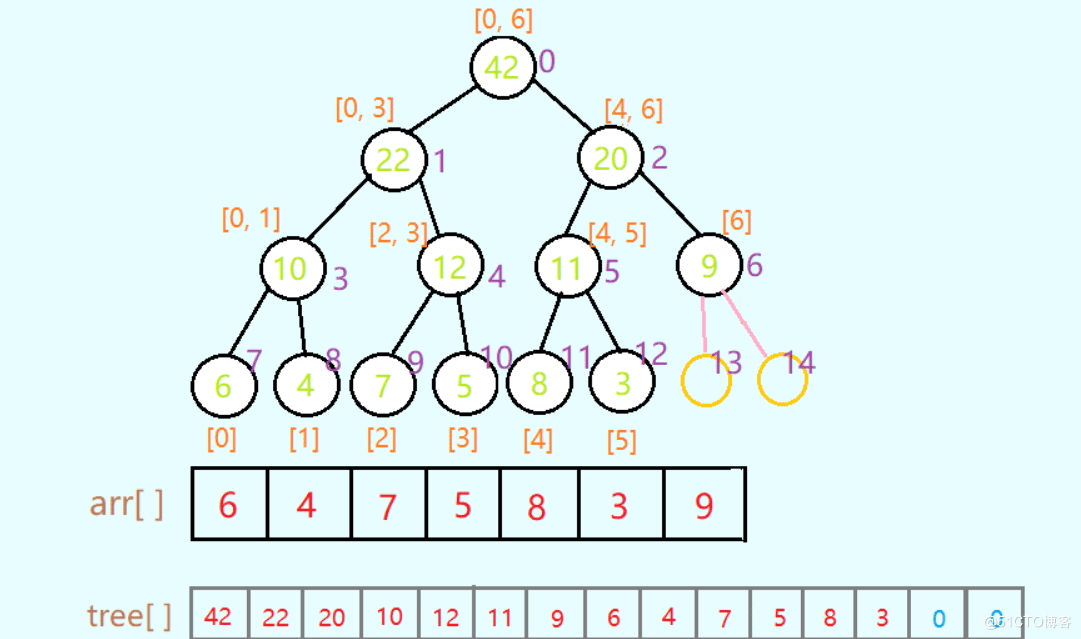
那么，如何用处程序来创建一棵树呢？

由于线段树叶子结点都是数组arr中的某一元素，所以我们可以使用两个变量low和high来标记数组arr的区间，

• 若low == high，此时令tree[node] = arr[low]，并终止递归
• 否则，将区间二分，分别计算左区间[low, mid]和右区间[mid +1, high],并在最后更新tree[node]

实现：

//创建树
public void buildTree() {
this.buildTree(0, 0, arr.length - 1);
}
private void buildTree(int node, int low, int high) {
if(low == high) {
tree[node] = arr[low];
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
buildTree(lnode, low, mid);
buildTree(rnode, mid + 1, high);
tree[node] = tree[lnode] + tree[rnode];
}

单点修改

若现在将arr[4]的值修改为1，需要怎样操作呢？

从下图绿色标出的结点不难看出其更新过程，先将其所对应的叶子结点修改，然后继续向上修改其父节点即可。

当long==high&&low==index时更新两个数组的值，否则，缩小区间，在相应的区间搜索，最后更新结点和即可，相应代码如下

//单点修改更新树
public void updateTree(int index, int val) {
this.updateTree(0, 0, arr.length - 1, index, val);
}
private void updateTree(int node, int low, int high, int index, int val) {
if(low == high && low == index) {
arr[index] = val;
tree[node] = val;
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
if(index >= low && index <= mid) {
updateTree(lnode, low, mid, index, val);
}else {
updateTree(rnode, mid + 1, high, index, val);
}
tree[node] = tree[lnode] + tree[rnode];
}

区间查找

若现在查找数组arr区间和[3,6]，如何利用线段树呢？

在线段树中，我们将它的和划分为两个区间[3]和[4,6]，如图中的黄色结点

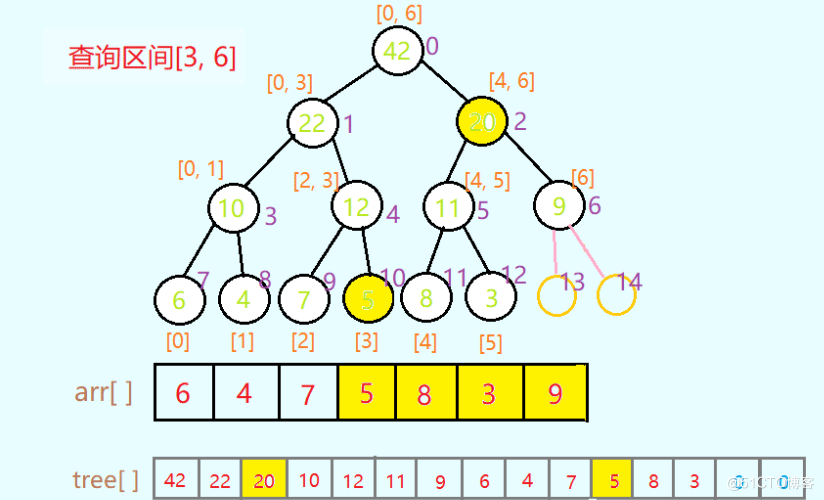
下面来看看相关代码如何实现，给定一个查找区间[L, R]，同样使用变量low和high维护对数组arr的二分查找边界

• 若当前区间low > R 或者 high < L，说明已超出查找范围，返回0
• 若[low, high]处于区间[L, R]内，返回当前结点的值tree[node]

然后继续在左右区间查找并保存左右区间的值sumLeft和sumRight，最后返回sumLeft + sumRight即可

//区间查找
public int queryTree(int L, int R) {
return this.queryTree(0, 0, arr.length - 1, L, R);
}
private int queryTree(int node, int low,
int high, int L, int R) {
if(low > R || high < L) {
return 0;
}else if(low >= L && high <= R) {
return tree[node];
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
int sumleft = queryTree(lnode, low, mid, L, R);
int sumRight = queryTree(rnode, mid + 1, high, L, R);
return sumleft + sumRight;
}

完整代码及测试

class SegmentTree{
private static final int[] tree = new int[1000];
int[] arr;
SegmentTree() {
}
SegmentTree(int[] arr) {
this.arr = arr;
}
//创建树
public void buildTree() {
this.buildTree(0, 0, arr.length - 1);
}
private void buildTree(int node, int low, int high) {
if(low == high) {
tree[node] = arr[low];
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
buildTree(lnode, low, mid);
buildTree(rnode, mid + 1, high);
tree[node] = tree[lnode] + tree[rnode];
}
//单点修改更新树
public void updateTree(int index, int val) {
this.updateTree(0, 0, arr.length - 1, index, val);
}
private void updateTree(int node, int low, int high, int index, int val) {
if(low == high && low == index) {
arr[index] = val;
tree[node] = val;
return;
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
if(index >= low && index <= mid) {
updateTree(lnode, low, mid, index, val);
}else {
updateTree(rnode, mid + 1, high, index, val);
}
tree[node] = tree[lnode] + tree[rnode];
}
//区间查找
public int queryTree(int L, int R) {
return this.queryTree(0, 0, arr.length - 1, L, R);
}
private int queryTree(int node, int low, int high, int L, int R) {
if(low > R || high < L) {
return 0;
}else if(low >= L && high <= R) {
return tree[node];
}
int mid = low + (high - low) / 2;
int lnode = 2 * node + 1;
int rnode = 2 * node + 2;
int sumleft = queryTree(lnode, low, mid, L, R);
int sumRight = queryTree(rnode, mid + 1, high, L, R);
return sumleft + sumRight;
}
//输出线段树的值
public void printTree() {
int size = 15; //size值的大小由arr数组的大小而定
for (int i = 0; i < size; i++) {
System.out.print(tree[i] + " ");
}
System.out.println();
}
}
public class SegmentTreeTest {
public static void main(String[] args) {
int[] arr = {6, 4, 7, 5, 8, 3, 9};
SegmentTree st = new SegmentTree(arr);
//创建线段树
st.buildTree();
st.printTree();
//>>>42 22 20 10 12 11 9 6 4 7 5 8 3 0 0
//查找区间[3, 6]
int sum = st.queryTree(3, 6);
System.out.println(sum);
//>>>25
//单点修改更新树, 令arr[4] = 1
st.updateTree(4, 1);
st.printTree();
//>>>35 22 13 10 12 4 9 6 4 7 5 1 3 0 0
}
}

树结点版本：

此版本不使用数组保存，而是以结点来保存值，相应代码不难实现，如下：

import java.util.ArrayDeque;
import java.util.Deque;
class SegNode{
int val;
SegNode lnode;
SegNode rnode;
SegNode(){}
SegNode(int val) {
this.val = val;
}
}
class SegTree{
SegNode root;
int[] arr;
SegTree() {}
SegTree(int[] arr) {
this.arr = arr;
this.bulidTree();
}
//创建树
public void bulidTree() {
root = this.buildTree(0, arr.length - 1);
}
private SegNode buildTree(int low, int high) {
if(low == high) {
return new SegNode(arr[low]);
}
SegNode node = new SegNode();
int mid = low + (high - low) / 2;
node.lnode = buildTree(low, mid);
node.rnode = buildTree(mid + 1, high);
node.val = node.lnode.val + node.rnode.val;
return node;
}
//单点修改更新树
public void updateTree(int index, int val) {
root = updateTree(root ,0, arr.length - 1, index, val);
}
private SegNode updateTree(SegNode node, int low, int high, int index, int val) {
if(low == high && low == index) {
arr[index] = val;
node.val = val;
return node;
}
int mid = low + (high - low) / 2;
if(index >= low && index <= mid) {
node.lnode = updateTree(node.lnode, low, mid, index, val);
}else {
node.rnode = updateTree(node.rnode, mid + 1, high, index, val);
}
node.val = node.lnode.val + node.rnode.val;
return node;
}
//查找区间
public int queryTree(int L, int R) {
return queryTree(root, 0, arr.length - 1, L, R);
}
private int queryTree(SegNode node, int low, int high, int L ,int R) {
if(low > R || high < L) {
return 0;
}else if(low >= L && high <= R) {
return node.val;
}
int mid = low + (high - low) / 2;
int sumLeft = queryTree(node.lnode, low, mid, L, R);
int sumRight = queryTree(node.rnode, mid + 1, high, L, R);
return sumLeft + sumRight;
}
//输出树(层次遍历)
public void printTree() {
Deque<SegNode> queue = new ArrayDeque<SegNode>();
queue.offer(this.root);
while(!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
SegNode node = queue.poll();
System.out.print(node.val + " ");
if(node.lnode != null) queue.offer(node.lnode);
if(node.rnode != null) queue.offer(node.rnode);
}
}
}
}
public class SegmentTreeNodeTest {
public static void main(String[] args) {
int[] arr = {6, 4, 7, 5, 8, 3, 9};
//创建线段树
SegTree st = new SegTree(arr);
st.printTree();
System.out.println("");
//>>>42 22 20 10 12 11 9 6 4 7 5 8 3
//查找区间[3, 6]
int sum = st.queryTree(3, 6);
System.out.println(sum);
//>>>25
//单点修改更新树, 令arr[4] = 1
st.updateTree(4, 1);
st.printTree();
System.out.println("");
>>>35 22 13 10 12 4 9 6 4 7 5 1 3
}
}

到此这篇关于C++高级数据结构之线段树的文章就介绍到这了,更多相关C++线段树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！