python基于三阶贝塞尔曲线的数据平滑算法

前言

很多文章在谈及曲线平滑的时候，习惯使用拟合的概念，我认为这是不恰当的。平滑后的曲线，一定经过原始的数据点，而拟合曲线，则不一定要经过原始数据点。

一般而言，需要平滑的数据分为两种：时间序列的单值数据、时间序列的二维数据。对于前者，并非一定要用贝塞尔算法，仅用样条插值就可以轻松实现平滑；而对于后者，不管是 numpy 还是 scipy 提供的那些插值算法，就都不适用了。

本文基于三阶贝塞尔曲线，实现了时间序列的单值数据和时间序列的二维数据的平滑算法，可满足大多数的平滑需求。

贝塞尔曲线

关于贝塞尔曲线的数学原理，这里就不讨论了，直接贴出结论：

一阶贝塞尔曲线

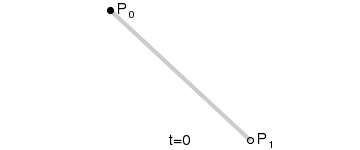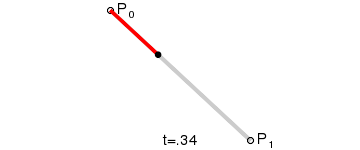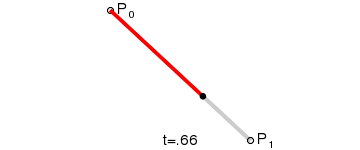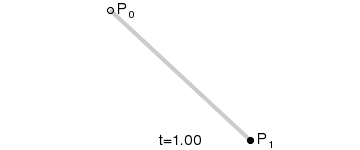
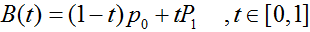
二阶贝塞尔曲线

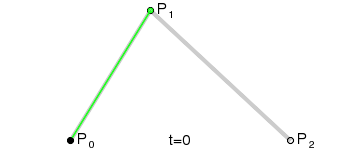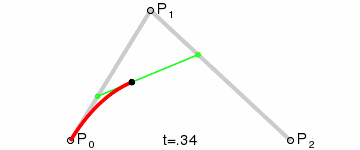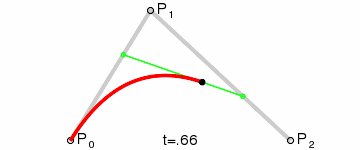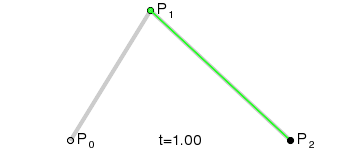
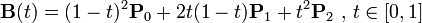
三阶贝塞尔曲线

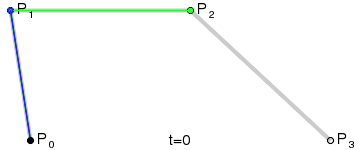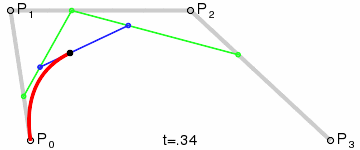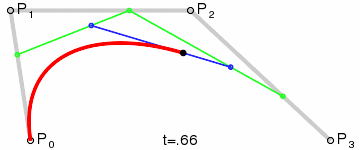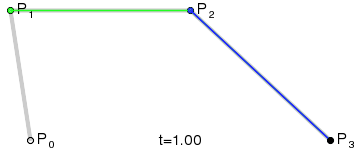
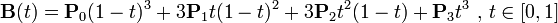
算法描述

如果我们把三阶贝塞尔曲线的 P0 和 P3 视为原始数据，只要找到 P1 和 P2 两个点（我们称其为控制点），就可以根据三阶贝塞尔曲线公式，计算出 P0 和 P3 之间平滑曲线上的任意点。

现在，平滑问题变成了如何计算两个原始数据点之间的控制点的问题。步骤如下：

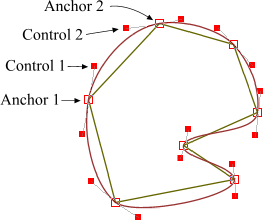
第1步：绿色直线连接相邻的原始数据点，计算出个线段的中点，红色直线连接相邻的中点

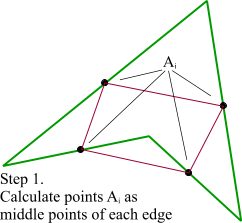
第2步：根据相邻两条绿色直线长度之比，分割其中点之间红色连线，标记分割点

第3步：平移红色连线，使其分割点与相对的原始数据点重合

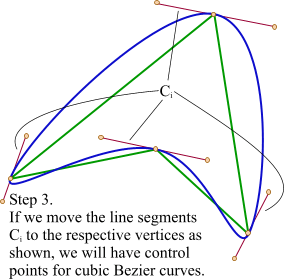
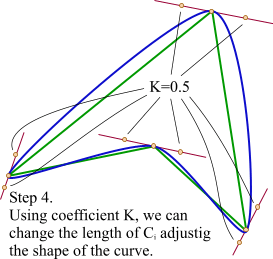
第4步：调整平移后红色连线的端点与原始数据点的距离，通常缩减40%-80%

算法实现

# -*- coding: utf-8 -*-

import numpy as np

def bezier_curve(p0, p1, p2, p3, inserted):
 """
 三阶贝塞尔曲线

 p0, p1, p2, p3 - 点坐标，tuple、list或numpy.ndarray类型
 inserted  - p0和p3之间插值的数量
 """

 assert isinstance(p0, (tuple, list, np.ndarray)), u'点坐标不是期望的元组、列表或numpy数组类型'
 assert isinstance(p0, (tuple, list, np.ndarray)), u'点坐标不是期望的元组、列表或numpy数组类型'
 assert isinstance(p0, (tuple, list, np.ndarray)), u'点坐标不是期望的元组、列表或numpy数组类型'
 assert isinstance(p0, (tuple, list, np.ndarray)), u'点坐标不是期望的元组、列表或numpy数组类型'

 if isinstance(p0, (tuple, list)):
  p0 = np.array(p0)
 if isinstance(p1, (tuple, list)):
  p1 = np.array(p1)
 if isinstance(p2, (tuple, list)):
  p2 = np.array(p2)
 if isinstance(p3, (tuple, list)):
  p3 = np.array(p3)

 points = list()
 for t in np.linspace(0, 1, inserted+2):
  points.append(p0*np.power((1-t),3) + 3*p1*t*np.power((1-t),2) + 3*p2*(1-t)*np.power(t,2) + p3*np.power(t,3))

 return np.vstack(points)

def smoothing_base_bezier(date_x, date_y, k=0.5, inserted=10, closed=False):
 """
 基于三阶贝塞尔曲线的数据平滑算法

 date_x  - x维度数据集，list或numpy.ndarray类型
 date_y  - y维度数据集，list或numpy.ndarray类型
 k   - 调整平滑曲线形状的因子，取值一般在0.2~0.6之间。默认值为0.5
 inserted - 两个原始数据点之间插值的数量。默认值为10
 closed  - 曲线是否封闭，如是，则首尾相连。默认曲线不封闭
 """

 assert isinstance(date_x, (list, np.ndarray)), u'x数据集不是期望的列表或numpy数组类型'
 assert isinstance(date_y, (list, np.ndarray)), u'y数据集不是期望的列表或numpy数组类型'

 if isinstance(date_x, list) and isinstance(date_y, list):
  assert len(date_x)==len(date_y), u'x数据集和y数据集长度不匹配'
  date_x = np.array(date_x)
  date_y = np.array(date_y)
 elif isinstance(date_x, np.ndarray) and isinstance(date_y, np.ndarray):
  assert date_x.shape==date_y.shape, u'x数据集和y数据集长度不匹配'
 else:
  raise Exception(u'x数据集或y数据集类型错误')

 # 第1步：生成原始数据折线中点集
 mid_points = list()
 for i in range(1, date_x.shape[0]):
  mid_points.append({
   'start': (date_x[i-1], date_y[i-1]),
   'end':  (date_x[i], date_y[i]),
   'mid':  ((date_x[i]+date_x[i-1])/2.0, (date_y[i]+date_y[i-1])/2.0)
  })

 if closed:
  mid_points.append({
   'start': (date_x[-1], date_y[-1]),
   'end':  (date_x[0], date_y[0]),
   'mid':  ((date_x[0]+date_x[-1])/2.0, (date_y[0]+date_y[-1])/2.0)
  })

 # 第2步：找出中点连线及其分割点
 split_points = list()
 for i in range(len(mid_points)):
  if i < (len(mid_points)-1):
   j = i+1
  elif closed:
   j = 0
  else:
   continue

  x00, y00 = mid_points[i]['start']
  x01, y01 = mid_points[i]['end']
  x10, y10 = mid_points[j]['start']
  x11, y11 = mid_points[j]['end']
  d0 = np.sqrt(np.power((x00-x01), 2) + np.power((y00-y01), 2))
  d1 = np.sqrt(np.power((x10-x11), 2) + np.power((y10-y11), 2))
  k_split = 1.0*d0/(d0+d1)

  mx0, my0 = mid_points[i]['mid']
  mx1, my1 = mid_points[j]['mid']

  split_points.append({
   'start': (mx0, my0),
   'end':  (mx1, my1),
   'split': (mx0+(mx1-mx0)*k_split, my0+(my1-my0)*k_split)
  })

 # 第3步：平移中点连线，调整端点，生成控制点
 crt_points = list()
 for i in range(len(split_points)):
  vx, vy = mid_points[i]['end'] # 当前顶点的坐标
  dx = vx - split_points[i]['split'][0] # 平移线段x偏移量
  dy = vy - split_points[i]['split'][1] # 平移线段y偏移量

  sx, sy = split_points[i]['start'][0]+dx, split_points[i]['start'][1]+dy # 平移后线段起点坐标
  ex, ey = split_points[i]['end'][0]+dx, split_points[i]['end'][1]+dy # 平移后线段终点坐标

  cp0 = sx+(vx-sx)*k, sy+(vy-sy)*k # 控制点坐标
  cp1 = ex+(vx-ex)*k, ey+(vy-ey)*k # 控制点坐标

  if crt_points:
   crt_points[-1].insert(2, cp0)
  else:
   crt_points.append([mid_points[0]['start'], cp0, mid_points[0]['end']])

  if closed:
   if i < (len(mid_points)-1):
    crt_points.append([mid_points[i+1]['start'], cp1, mid_points[i+1]['end']])
   else:
    crt_points[0].insert(1, cp1)
  else:
   if i < (len(mid_points)-2):
    crt_points.append([mid_points[i+1]['start'], cp1, mid_points[i+1]['end']])
   else:
    crt_points.append([mid_points[i+1]['start'], cp1, mid_points[i+1]['end'], mid_points[i+1]['end']])
    crt_points[0].insert(1, mid_points[0]['start'])

 # 第4步：应用贝塞尔曲线方程插值
 out = list()
 for item in crt_points:
  group = bezier_curve(item[0], item[1], item[2], item[3], inserted)
  out.append(group[:-1])

 out.append(group[-1:])
 out = np.vstack(out)

 return out.T[0], out.T[1]

if __name__ == '__main__':
 import matplotlib.pyplot as plt

 x = np.array([2,4,4,3,2])
 y = np.array([2,2,4,3,4])

	plt.plot(x, y, 'ro')
 x_curve, y_curve = smoothing_base_bezier(x, y, k=0.3, closed=True)
 plt.plot(x_curve, y_curve, label='$k=0.3$')
 x_curve, y_curve = smoothing_base_bezier(x, y, k=0.4, closed=True)
 plt.plot(x_curve, y_curve, label='$k=0.4$')
 x_curve, y_curve = smoothing_base_bezier(x, y, k=0.5, closed=True)
 plt.plot(x_curve, y_curve, label='$k=0.5$')
 x_curve, y_curve = smoothing_base_bezier(x, y, k=0.6, closed=True)
 plt.plot(x_curve, y_curve, label='$k=0.6$')
 plt.legend(loc='best')

 plt.show()

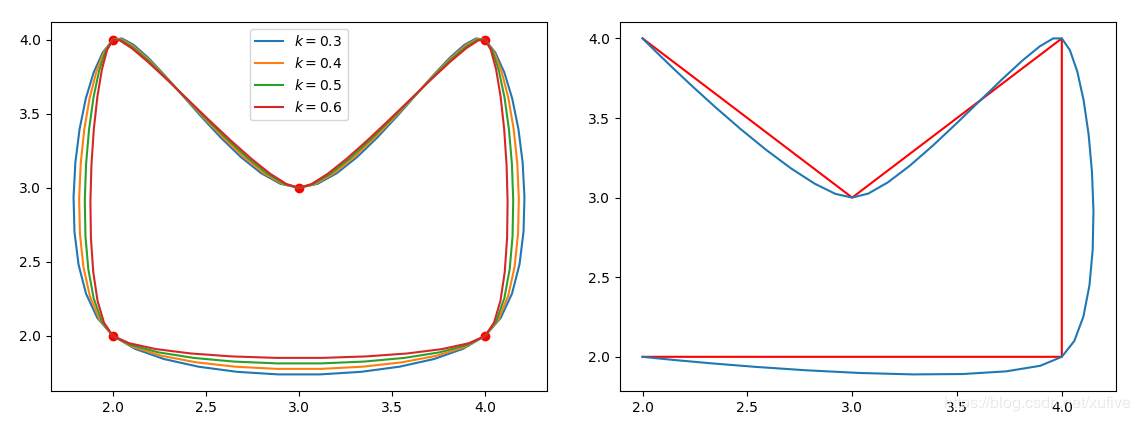
下图为平滑效果。左侧是封闭曲线，两个原始数据点之间插值数量为默认值10；右侧为同样数据不封闭的效果，k值默认0.5.

参考资料

算法参考了 Interpolation with Bezier Curves 这个网页，里面没有关于作者的任何信息，在此只能笼统地向国际友人表示感谢！

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。