Numpy实现矩阵运算及线性代数应用

一、创建矩阵的方法

import numpy as np
# 1直接创建
mat=np.mat("1 2 3;4 5 6;7 8 9")
print(mat)
# 2使用numpy数组创建矩阵
mat2=np.mat(np.arange(1,10).reshape(3,3))
print(mat2)
# 3从已有的矩阵中通过bmat函数创建
A=np.eye(2)
B=A*2
mat3=np.bmat("A B;B A")
print(mat3) #类似于拼接

二、矩阵运算

2.1随机函数表

随机函数1

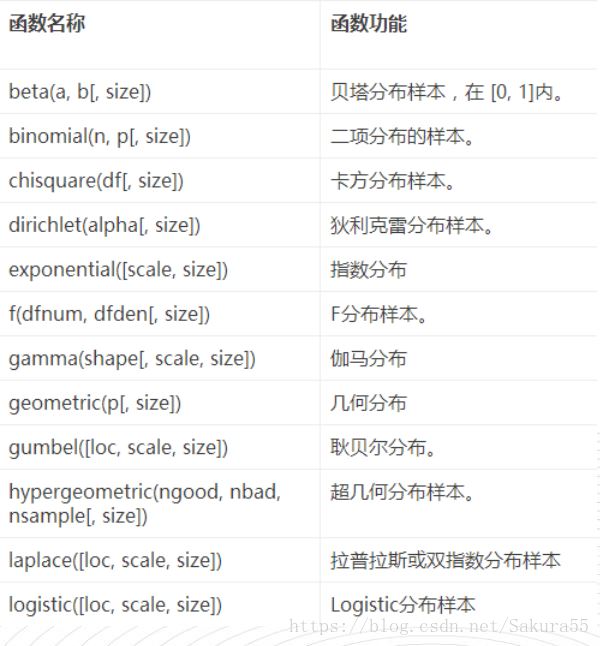
随机函数2*

2.2部分实例

mat1=np.mat(np.array([2,6,5]))
mat2=np.mat(np.array([2,6,5]))

2.2.1加法—np.add

addresult=np.add(mat1,mat2)
print(addresult)

2.2.2乘法—multiply

multiresult=np.multiply(mat1,mat2)
print(multiresult) #数值的乘法
mat3=np.mat(np.arange(6).reshape(2,3))
mat4=np.mat(np.arange(6).reshape(3,2))
print("mat3*mat4\n",mat3*mat4)

2.2.3除法—divide

a=np.mat(np.array([4,5,8]))
b=np.mat(np.array([2,3,5]))
#########################除法
result1=np.divide(a,b)
print(result1)

#数组除法将结果向下去整
result2=np.floor_divide(a,b)
print("除法向下去整：",result2)
#矩阵直接相除
print("矩阵直接相除",a/b)
#矩阵取模
print("矩阵取模",a%b)

#返回小数部分
floatResult=np.true_divide(a,b)
print(floatResult)

mat**2，要求mat为方阵，其平方为mat*mat的结果
mat1*mat2的结果为mat1(m,n)的行与mat2(n,p)的列乘积组成的新的矩阵(m,p)

2.2.4取模-mod/fmod

import numpy as np
mat1=np.mat(np.array([5,-7,9]))
mat2=np.mat(np.array([2,-4,3]))
#取模运算
result1=np.remainder(mat1,mat2)
print("remainder:",result1)

result2=np.mod(mat1,mat2)
print("mod",result2)

result3=mat1%mat2
print("%",result3)

result4=np.fmod(mat1,mat2)
print(result4) #模 的正负和被除数相同，与除数无关

三、通用函数

1一元函数（ufunc），只接受一个数组，结果返回一个结果数组，
当然也有返回两个数组的（modf），但是情况很少。
2二元函数（binary）,接受的是两个结果，返回的是一个结果数组

3.1 一元通用函数

3.1.1 图表总说明

红线圈出为常用函数

import numpy as np
mat=np.mat(np.array([-10,5,-4,3,0,12]))
print(np.abs(mat)) #绝对值
print(np.fabs(mat)) #非复数情况下

3.1.2获取矩阵中各元素的正负—sign

#获取矩阵中各元素的正负号
sign=np.sign(mat)
print("sign:",sign)
#sign: [[-1 1 -1 1 0 1]]

3.1.3整数小数的抽取分离—modf

#将数组中元素的小数和整数部分抽取出来
arr=np.array([[1.2,3.34],
    [-2.5,6.8]])
arr1,arr2=np.modf(arr)
print("整数部分：",arr2)
print("小数部分：",arr1)

3.2二元通用函数

3.2.1图表总说明

红线圈出为常用函数

3.2.2对应的矩阵的幂函数运算—power

mat2=np.mat(np.array([1,2,3,4]))
mat3=np.mat(np.array([2,3,2,3]))
result1=np.power(mat2,mat3) #mat2中元素作为底，mat3作为幂
print(result1)

3.2.3获取两个数组中对应元素的最大/小值，存放到新的数组中power()

import numpy as np
mat3=np.mat(np.array([[1,2.2],[2,1.2]]))
mat4=np.mat(np.array([[5,2.6],[2,3.2]]))
result=np.power(mat1,mat2)
print(result) >> [[ 1.   20.57737365] [ 6.76  1.79217324]]

maximun=np.maximum(mat3,mat4)
print(maximun) >> [[5. 2.6] [2. 3.2]]

3.2.4数组比较—greater

result2=np.greater(mat3,mat4)
print(result2) >> [[False True] [ True False]]
# 亦或 xor：相同的为False，不同的为True

3.2.5创建同结构的数组—np.zeros_like()

import numpy as np
a=np.arange(4).reshape(2,2)
print(a)
#创建一个和a类型一样，但数据全是0的数组
like_a=np.zeros_like(a)
like_a=3 #赋值
print(like_a)
#################################################################################
#创建一个通用函数numpy
def like(ndarry):
 result=np.zeros_like(ndarry)
 result.flat=5
 return result
#调用numpy创建通用函数的方法,1个输入，一个输出
myfunc=np.frompyfunc(like,1,1)
test=myfunc(np.arange(9).reshape(3,3))
print(test)
#结果如下：
#[[array(5) array(5) array(5)]
# [array(5) array(5) array(5)]
# [array(5) array(5) array(5)]]

四、矩阵运算-add运算

4.1矩阵元素求和—reduce

print("reduce:",np.add.reduce(a))
print("sum:",np.sum(a))

4.2矩阵元素求和列出—accumulate

print("accumulate",np.add.accumulate(a))

4.3reduceat函数

print("reduceat",np.add.reduceat(a,[1,3,2,4])) # >> reduceat [3 3 5 4]
 #第一步用到索引值列表中的1和3，对数组中索引值在1到3之间的元素进行reduce操作 得到3;
 #第二步用到索引值3和2。由于2比3小，所以直接返回索引值为3的元素 得到3;
 #第三步用到索引值2和4。对索引值在2到4之间的数组元素进行reduce操作 得到4;
 #第四步用到索引值4。对索引值从7开始直到数组末端的元素进行reduce操作 得到5;

4.4各个矩阵元素相加—outer

arr1=np.array([1,6])
arr2=np.array([2,3,5,65])
result2=np.add.outer(arr1,arr2) #相加
result3=np.outer(arr1,arr2)  #相乘
print("outer:",result2)
 # outer 将第一个数组中的每个元素分别和第二个数组的所有元素相加

五、线性代数的应用

5.1 逆矩阵—np.linalg.inv()

import numpy as np
A=np.mat(np.array([[0,1,2],[1,0,3],[4,-3,8]]))
#求A 的逆矩阵
A_=np.linalg.inv(A)
print("A的逆矩阵：\n",A_)

#验证A*A_是否是单位矩阵
print("A*A_:\n",A*A_)

5.2计算矩阵—np.linalg.solve(arr1,arr2)

import numpy as np

'''
X-2Y+Z=0
2Y-8Z=8
-4X+5Y+9Z=-9
'''
#求解三元一次函数
A=np.mat("1 -2 1;0 2 -8;-4 5 9")
print("系数：",A)
B=np.array([0,8,-9])
print("常数:",B)

#调用numpy的solve方法
result=np.linalg.solve(A,B)
print("X={},Y={},Z={}".format(result[0],result[1],result[2]))

5.3 特征值和特征向量

import numpy as np
vector=np.mat("3 -2;1 0")
#求特征值
eigenvalues=np.linalg.eigvals(vector)
# 特征值是Ax=ax的根
eigenvalues,eigvector=np.linalg.eig(vector)
print("特征值：",eigenvalues)
print("特征向量：\n",eigvector)
>>结果：
特征值： [2. 1.]
特征向量：
 [[0.89442719 0.70710678]
 [0.4472136 0.70710678]]

5.4奇异值分解—np.linalg.svd()

import numpy as np
vector=np.mat("4 11 14;8 7 -2")
#调用numpy汇总的svd方法对矩阵进行奇异值分解
U,sigma,V=np.linalg.svd(vector,full_matrices=False)
print("U\n",U)
print("sigma:\n",sigma)
print("V:\n",V)

#将svd分解出的值相乘
print("vector:\n",U*np.diag(sigma)*V)

5.5矩阵行列式—np.linalg.det()

对于一个n×n的实数矩阵，行列式描述的是一个线性变换对“有向体积”所造成的影响。行列式的值为正表示保持了空间的定向（顺时针或逆时针），为负则表示颠倒了空间的定向。numpy.linalg模块中的det函数可以计算矩阵的行列式。

import numpy as np
vector=np.mat("3 4;5 6")
print(vector)
#求行列式
value=np.linalg.det(vector)
print("行列式：",value)

六、专用函数

6.1排序

6.1.1对数组元素进行排序

import numpy as np
arr=np.array([1,2,34,5])
result=np.sort(arr)
arr.sort()
print(arr)

6.1.2返回排序后数组元素的索引—argsort()

argsort=np.argsort(arr)
print("argsort:",argsort)
d2=np.array([[12,3,45,2],
    [43,552,1,9]])
#将多维数组按列排序
d2.sort(axis=0)
print(d2)
#[[ 12 3 1 2]
# [ 43 552 45 9]]
#将多维数组按行排序
d2.sort(axis=1)
print(d2)

6.1.3竖向索引排序

print(np.argsort(d2,axis=0))
[[0 0 0 0]
 [1 1 1 1]]

6.1.4横向索引排序

print(np.argsort(d2,axis=1))
[[2 3 1 0]
[3 0 2 1]]

6.2搜索函数

6.2.1基本函数

6.2.2获取最大值的下标—np.argmax()

import numpy as np
a=np.array([[2,3,653,4],
   [5,62,943,44,]])
b=np.array([32,13,65,43])
#如果是多维数组，则将多维数组展平后获取最大值的下标
argmax=np.argmax(a)
print(argmax)

6.2.3非零元素获取下标—np.argwhere()

#根据条件数组中搜索非零的元素，分析返回对应的下标
print("argwhere\n",np.argwhere(b>40))
print("argwhere 多维\n",np.argwhere(a>100))
'''
argwhere 多维
 [[0 2]
 [1 2]]
'''

6.2.4寻找合适的下标—np.searchsorted()

sorted=np.arange(5)
indices=np.searchsorted(sorted,[-2,7])
print(indices)      #下标

6.2.5添加符合的下标的元素，返回新的数组—np.searchsorted()

newsorted=np.insert(sorted,indices,[-2,7])
print("添加新元素后：\n",newsorted)

6.3抽取函数—extract(condition,ndarray)

一维

import numpy as np
a=np.arange(10)
#生成一个抽取元素的花式索引
condition=a%2==0#赋值/算术/逻辑运算符优先级
print("花式索引",condition)
even=np.extract(condition,a)
print("偶数项：",even)
#take()/compress()
even2=a.compress(condition)

多维强调内容

import numpy as np
#抽取数组中非零的元素np.nonzero() 的索引
arr=np.array([[0,1,2],[0,3,4],[0,5,6]])
rows,cols=np.nonzero(arr)
print("rows",rows)
print("cols:",cols)

indices=np.dstack((rows,cols))
print("indices:\n",indices)

6.4金融函数

6.4.1 计算存款/贷款（终值）—fv函数

np.fv(rate,nper,pmt,pv,)
rate:存款/贷款每一期的利率
nper：总期数
pmt：存款/贷款支付的金额
pv：存款/贷款金额
rate=0.03/4
nper=5*4
pmt=-10
pv=-1000

import numpy as np
#某用户去银行存款，假设年利率是3%,，每季度存10元，
# 存5年以及存款1000，五年后可得到的本息和是多少？

#g该用户5年后得到的本息为
fv=np.fv(0.03/4,5*4,-10,-1000)
print("5年后本息和：",fv)
#计算每一年的本息和
for i in range(1,6):
 fv1=np.fv(0.03/4,i*4,-10,-1000)
 print("第",i,"年本息和为：{}".format(fv1))

6.4.2计算首月的金额(起始值)—pv函数

np.pv(rate, nper, pmt, pv, )
如果是贷款则是终值0
如果是贷款是本息和

import numpy as np
#存五年可得1376.0963320407982，计算5年前存款的金额
pv=np.pv(0.03/4,5*4,-10,1376.0963320407982)
print("5年钱第一次存款的金额是：",np.round(-pv))

6.4.3计算净现值—npv函数

np.npv(rate,value)
rate:折现率
values:现金流
NPV>0，则除了得到预定的收益率外，可能得到更高的收益；
NPV<0，则未达到利益水平，但是不能确定自己是否亏损；
NPV=0， 正好达到预期的收益效果 ，不是盈亏平衡

#投资100，支出39，59，55，20，折现率28.1%，净现值多大？
npv=np.npv(0.281,[-100,39,59,55,20])
print("净现值：",npv)

6.4.4计算每期还款金额—pmt函数

np.pmt(rate,nper,pv)
rate: 存款 / 贷款每一期的利率
nper：总期数
pv:需要还款的金额

#某人贷款20万，15年还清，年利率是7.5%，求每月还的金额？
pmt=np.pmt(0.075/12,15*12,200000)
print("每月还款的金额：{}".format(pmt))

6.4.5计算还款期数—nper函数

np.nper(rate,pmt,pv,fv)
rate:存款/贷款每一期的利率
pmt：存款/贷款支付的金额
pv：存款/贷款金额
fv:总金额

#某人贷款20万，每月还2000，年利率是7.5%，求多少年还完？
nper=np.nper(0.075/12,-2000,200000)
months=np.ceil(nper)
years=np.ceil(months/12)#向上取整
print("需要还款{}年".format(years)) >>14年

到此这篇关于Numpy实现矩阵运算及线性代数应用的文章就介绍到这了,更多相关Numpy 矩阵运算及线性代数内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！