关于pytorch相关部分矩阵变换函数的问题分析

目录

• 1、tensor 维度顺序变换 BCHW顺序的调整
• 2、矩阵乘法相关函数，矩阵乘，点乘
• 3、求取矩阵对角线元素，或非对角线元素

1、tensor 维度顺序变换 BCHW顺序的调整

tensor.permute(dims)

将tensor的维度换位。参数是一系列的整数，代表原来张量的维度。比如三维就有0，1，2这些dimension。

import torch
a = torch.rand(8,256,256,3)   #---> n,h,w,c
print(a.shape)
b = a.permute(0,3,1,2)  # ---> n,c,h,w
print(b.shape)
#输出
torch.Size([8, 256, 256, 3])
torch.Size([8, 3, 256, 256])

numpy内进行维度顺序变换采用_numy.transpose(a,axis=None)_

参数 a: 输入数组

axis: int类型的列表，这个参数是可选的。默认情况下，反转的输入数组的维度，当给定这个参数时，按照这个参数所定的值进行数组变换。

返回值 p: ndarray 返回转置过后的原数组的视图。

import numpy as ?np
?
x = np.random.randn(8,256,256,3) ?# ---> n,h,w,c
print(x.shape)
y=x.transpose((0,3,1,2)) ? # ?----> n,c,h,w
print(y.shape)

#输出
(8, 256, 256, 3)
(8, 3, 256, 256)

2、矩阵乘法相关函数，矩阵乘，点乘

二维矩阵乘法torch.mm()

torch.mm(mat1,mat2,out=None),其中mat1(NXM)，mat2(MXD)，输出out的维度为(NXD)

该函数一般只用来计算两个二维矩阵的矩阵乘法，并且不支持broadcast操作。

三维带batch的矩阵乘法 torch.bmm()
由于神经网络训练一般采用mini-batch，经常输入的时三维带batch的矩阵，所以提供torch.bmm(bmat1, bmat2, out=None)，其中bmat1(b×n×mb×n×m)，bmat2(b×m×db×m×d)，输出out的维度是(b×n×db×n×d)。

该函数的两个输入必须是三维矩阵且第一维相同（表示Batch维度），不支持broadcast操作。

多维矩阵乘法 torch.matmul()
torch.matmul(input, other, out=None)支持broadcast操作，使用起来比较复杂。

针对多维数据 matmul()乘法，我们可以认为该matmul()乘法使用使用两个参数的后两个维度来计算，其他的维度都可以认为是batch维度。假设两个输入的维度分别是input(1000×500×99×111000×500×99×11), other(500×11×99500×11×99)那么我们可以认为torch.matmul(input, other, out=None)乘法首先是进行后两位矩阵乘法得到(99×11)×(11×99)(99×99)(99×11)×(11×99)(99×99) ，然后分析两个参数的batch size分别是 (1000×500)(1000×500) 和 500500 , 可以广播成为 (1000×500)(1000×500)， 因此最终输出的维度是(1000×500×99×991000×500×99×99)。

矩阵逐元素(Element-wise)乘法 torch.mul()
torch.mul(mat1, other, out=None)，其中other乘数可以是标量，也可以是任意维度的矩阵，只要满足最终相乘是可以broadcast的即可

@ ：矩阵乘法，自动执行适合的矩阵乘法函数
* ：element-wise乘法

3、求取矩阵对角线元素，或非对角线元素

取对角线元素可以用torch.diagonal()

x = torch.randn(4,4)
# tensor([[ 0.9148,  0.1396, -0.8974,  2.0014],
#        [ 0.1129, -0.3656,  0.4371,  0.2618],
#        [ 1.1049, -0.0774, -0.4160, -0.4922],
#        [ 1.3197, -0.2022, -0.0031, -1.3811]])

torch.diagonal(x)
# tensor([ 0.9148, -0.3656, -0.4160, -1.3811])

非对角线元素没有特定API，如果是求和，可以矩阵求和 减去对角线元素和 。

网上看到一个巧妙的非对角线元素方法

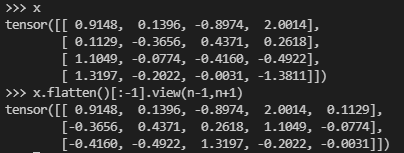
n, m = x.shape
assert n == m
x.flatten()[:-1].view(n-1,n+1)[:,1:].flatten()
# tensor([ 0.1396, -0.8974,  2.0014,  0.1129,  0.4371,  0.2618,  1.1049, -0.0774,
#        -0.4922,  1.3197, -0.2022, -0.0031])

首先利用flatten()拉直向量，然后去掉最后一个元素，得到n^2 - 1个元素，然后构造为一个维度为[N-1, N+1]的矩阵。在这个矩阵中，之前所有的对角线元素全部出现在第1列，然后根据索引获取[:, 1:]元素，得到的就是原矩阵的非对角线元素。

到此这篇关于pytorch相关部分矩阵变换函数的文章就介绍到这了,更多相关pytorch矩阵变换函数内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！