Python利用蒙特卡罗模拟期权定价
目录
- 期权,及其价值
- 风险中性估值
- 模拟资产价格
- 期权定价
- 为真实期权定价
- 完整的模拟
期权是一种合约,它赋予买方在未来某个时间点以特定价格买卖资产的权利。 这些被称为衍生品的合约的交易有多种原因,但一种常见的用法是来对冲当资产价格以不利方式变动,所产生的风险敞口。
期权,即买入或卖出的权利,也是有价格的。 Black Scholes 模型描述了一种确定期权公平价格的方法,但还有许多其他方法可以确定价格。
期权,及其价值
欧式期权只有在未来达到预定日期(称为到期日)后才能使用(或行使),可以用字母 T 表示。
看涨期权赋予期权持有人以已知价格购买的权利。 如果资产的到期价格(用 ST 表示)高于执行价格 K ,则看涨期权会赚钱,否则就一文不值。
CT=max(0,ST−K)
同样,看跌期权是出售资产的权利。 当资产在到期日价格ST低于执行价格K时,看跌期权会赚钱,否则就一文不值。
PT=max(0,K−ST)
以下是到期时看跌期权和看涨期权的收益图。 我们的资产价格是 x 轴,收益是 y 轴。
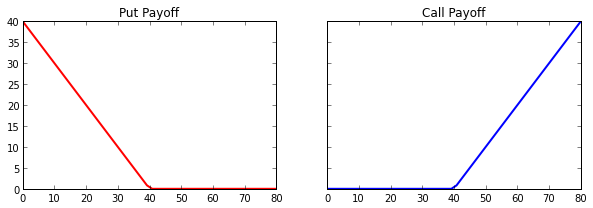
风险中性估值
为了使用蒙特卡罗模拟为期权定价,我们使用风险中性估值,其中衍生品的公允价值是其未来收益的预期价值。
因此,在到期前的任何日期,用 t 表示,期权的价值是其到期收益预期的现值 T 。
Ct=PV(E[max(0,ST−K)])
Pt=PV(E[max(0,K−ST)])
在风险中性估值下,我们假设标的资产将平均获得无风险利率。 因此,要计算任何时间 t 的期权收益,我们要按该利率对收益进行贴现。 现在我们有一种计算现值 PV 的方法。

上面的公式中,除了St ,所有这些变量都是已知的,因此St是我们的模拟将提供的。
为了给期权定价,我们将创建一个模拟,为资产 St 最终价格提供许多观察结果。 通过平均所有的回报,我们得到了对回报的期望值。
模拟资产价格
Black Scholes 模型中使用的股票价格行为模型假设我们有一个已知的波动性,我们有一个无风险利率,并且资产的价格遵循几何布朗运动。
几何布朗运动是一个随机过程,其中随机变量的对数服从正态分布。 这种类型的过程通过对数正态分布来分配价格。
所以现在我们有一个计算时间 T 时刻资产价格的方法:

为此,我们需要知道:
r 是我们要贴现的无风险利率。 σ 是波动率,即股票回报的年化标准差。 (T-t) 给了我们年化的到期时间。 例如,对于 30 天选项,这将是 30/365=0.082... S 是在时间 t 标的资产的价格。 ϵ 是我们的随机值。 它的分布必须是标准正态(均值为 0.0,标准差为 1.0)
期权定价
为了在模拟过程中为期权定价,我们生成资产可能在到期时的许多价格,计算每个生成价格的期权收益,将它们平均,然后对最终价值进行贴现。
在创建完整模拟之前,我们将通过一个包含10次运行的小示例。假设我们有一个具有以下价值的资产:S = 100.00 美元和 σ = 20%,我们想为半年到期的看涨期权定价,执行价为 110.00 美元,我们的无风险利率是 1%。
| 随机变量 | 资产价格 | 收益 | 贴现收益 |
|---|---|---|---|
| 1.3620 | 120.64 | 10.64 | 10.58 |
| -0.7784 | 89.13 | 0.00 | 0.00 |
| -0.9408 | 87.11 | 0.00 | 0.00 |
| 0.2227 | 102.69 | 0.00 | 0.00 |
| -0.0364 | 98.99 | 0.00 | 0.00 |
| -1.4303 | 81.28 | 0.00 | 0.00 |
| -0.8306 | 88.47 | 0.00 | 0.00 |
| 1.5155 | 123.28 | 13.28 | 13.21 |
| -1.5679 | 79.71 | 0.00 | 0.00 |
| -1.6718 | 78.55 | 0.00 | 0.00 |
将折扣收益值平均,得出我们的看涨期权价格为 2.38 美元。 我们执行的模拟越多,价格就越准确。
现在我们可以看到模拟如何生成价格,让我们构建一个可以为期权定价的小型 Python 脚本,看看它是否与真实情况相符。 让我们看一下实际的例子。
为真实期权定价
在下图中,我们有一个谷歌看涨期权的报价,行使价为 860.00 美元,将于 2013 年 9 月 21 日到期。我们还可以看到它的最后交易价格是14.50 美元。这个例子给了我们尝试定价时,期权的一个目标价格。
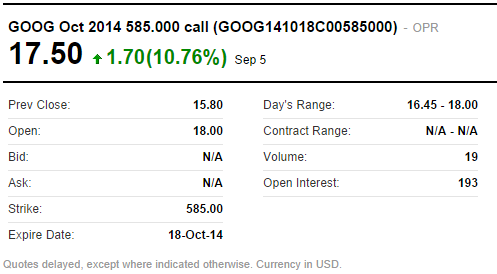
此处未指定的是波动性、无风险利率、当前的股票价格。 波动率是一个相当复杂的话题,因此就本文而言,我们将假设我们知道该特定期权的波动率为 20.76%。而股票当前价格可以通过查看各种来源找到,为857.29 美元。
对于无风险利率,我们可以使用与我们选择的到期时间相同的美国 LIBOR 利率; 我们的期权在大约三周后到期,由于没有三周利率,我们将使用两周利率来近似,即 0.14%。
接下来是Python代码的实现,首先我们将写下我们将如何生成资产价格。
def generate_asset_price(S,v,r,T):
return S * exp((r - 0.5 * v**2) * T + v * sqrt(T) * gauss(0,1.0))
我们知道所有的输入值,所以我们可以像这样设定它们:
S = 857.29 # underlying price v = 0.2076 # vol of 20.76% r = 0.0014 # rate of 0.14% T = (datetime.date(2013,9,21) - datetime.date(2013,9,3)).days / 365.0 print generate_asset_price(S,v,r,T) >>> 862.1783726682384
现在我们需要能够计算这个生成价格的回报。 回想一下之前我们说过看涨期权在到期时价值是 ST-K 或 0,我们将其表示为一个函数,并应用于我们生成的资产价格。
def call_payoff(S_T, K):
return max(S_T - K, 0.0)
print call_payoff(862.18, 860)
>>> 2.1799999999
完整的模拟
现在让我们将各模块代组合,并为 Google 期权定价。
import datetime
from random import gauss
from math import exp, sqrt
def generate_asset_price(S,v,r,T):
return S * exp((r - 0.5 * v**2) * T + v * sqrt(T) * gauss(0,1.0))
def call_payoff(S_T,K):
return max(0.0,S_T-K)
S = 857.29 # underlying price
v = 0.2076 # vol of 20.76%
r = 0.0014 # rate of 0.14%
T = (datetime.date(2013,9,21) - datetime.date(2013,9,3)).days / 365.0
K = 860.
simulations = 90000
payoffs = []
discount_factor = math.exp(-r * T)
for i in xrange(simulations):
S_T = generate_asset_price(S,v,r,T)
payoffs.append(
call_payoff(S_T, K)
)
price = discount_factor * (sum(payoffs) / float(simulations))
print 'Price: %.4f' % price
程序运行结果如下,这与我们在市场上观察到的此 Google 期权的价格相匹配。
Price: 14.5069
需要注意的是,我们刚刚计算的谷歌期权实际上是一个美式期权,我们只是把它定价成欧式期权,没有考虑期权可以提前行权的可能性,尽管如此,我们仍然得出了正确的价格。
这是因为,非派息股票(例如文中举例的 Google)的美式看涨期权的价格与欧式看涨期权的价格相同。理论上,当股票不支付股息时,提前行权并不是最佳选择。 如果期权永远不会提前行权,那么美式期权的价格可以像欧式期权一样进行计算。
到此这篇关于Python利用蒙特卡罗模拟期权定价 的文章就介绍到这了,更多相关Python期权定价 内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

