C语言动态规划点杀dp算法LeetCode炒股习题案例解析

目录

• 概念
• 性质
• 典型特征
• 实战论证
• 算法实现
• 优化

概念

说到动态规划，什么是动态规划？

动态规划（英语：Dynamic programming，简称 dp）通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

看着这么复杂哈，其实总结出来就是大事化小，拆分成小问题但是这些小问题和原问题是同质的，动规致力于解决每一个子问题，减少计算，其实和递归思想，分治法有些类似，斐波那契数列就可以看做入门级的经典动规问题

这里引用一个网上流行的例子来给大家体会一下：

A ：“1+1+1+1+1+1+1+1 =？”
A ：“上面等式的值是多少”
B ：计算 “8”
A : 在上面等式的左边写上 “1+” 呢？
A : “此时等式的值为多少”
B : 很快得出答案 “9”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”

性质

1.最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理（说人话就是切大瓜，切到最小又不影响我体验）

2.有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到（说人话就是藕断丝连，拿一个可能带动其他）

3.无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关（说人话就是把水化成冰，但本质上依然是水）

典型特征

动态规划有4个典型特征：

1.最优子结构

2.状态转移方程

3.边界

4.重叠子问题

以我们熟悉的斐波那契数列为例

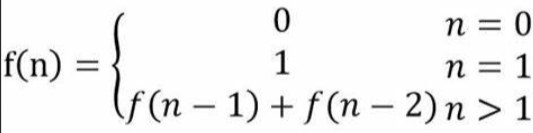
f(n-1)和f(n-2) 称为 f(n) 的最优子结构，f(n)= f（n-1）+f（n-2）就称为状态转移方程，f(1) = 1, f(2) = 2 称为边界，其中f(5)= f(4)+f(3),f(4) = f(3) + f(2) ,f(3)就是重叠子问题。

实战论证

要学习dp算法就一定得谈谈 LeetCode 里面的鼻祖题——炒股系列问题，我们就拿例题来港港怎么理解他的典型特征

初始题比较简单，我们以 II 为例：

示例：
输入: prices = [7,1,5,3,6,4]
输出: 7

小捷径

看到这里其实最简单的方法已经明了了，那就是贪心算法，只要能赚，只要不赔我就买买买！你说我贪不贪心？

int maxProfit(int* prices, int pricesSize) {
    int sum = 0;
    for (int i = 1; i < pricesSize; ++i) {
        sum += fmax(0, prices[i] - prices[i - 1]);
    }
    return sum;
}

这里用了一个库函数 fmax ，需要引头文件<math.h>，用于比较两个参数的最大值，语法是：

type fmax  (参数1 , 参数2);

再介绍一种我自己用的方法，和贪心原理上差不多，只是用的普普通通的遍历：

int maxProfit(int* prices, int pricesSize) {
	int n = 0;
	if (pricesSize == 0)
	{
		return 0;
	}
	int sum = 0;
	while (n < pricesSize - 1)
	{
		for (n = 0; n < pricesSize - 1; n++)
			if (prices[n + 1] - prices[n] > 0)//保证买卖能赚就入手
			{
				sum += prices[n+1]-prices[n];
			}
	}
	return sum;
}

我自己的方法还是比较优的

这样就能一套带走，但我们要用 dp 去搞定他，dp 其实也很简单，只是看着有点复杂，咱不能望而却步是吧。

分析条件，题目中说不能多次买卖，那我们有且只有两种状态就是没有和有一支，没有就是手里为0，又有两种可能就是前一天就是 0 和这一天有一支但被卖出去了；同理，有一支的情况就是前一天就有一支和前一天两手空空但我今天买进了一支。以此我们写出求最大利润的状态转移方程( i 从 0 开始)：

第i天有0支股票：dp[i][0] = dp[i-1][0] + dp[i][1]+prices[i];
第i天有1支股票：dp[i][1] = dp[i-1][1] + dp[i-1][0]-prices[i];

状态转移方程写出来了，题目就迎刃而解了

算法实现

1、借助数组或者二维数组，保存每一个子问题的结果，具体创建数组还是二维数组看题目而定，比如找零钱问题中的不同面值零钱与总钱数，这样就需要创建一个二维数组

2、对应题干条件，具体要求来设置数组边界值,一维数组就是设置第一个数字，二维数组就是设置第一行跟第一列的值

3、找出状态转换方程，找到每个状态跟他上一个状态的关系，根据状态转化方程就可以写出代码

我们用刚刚推出来的状态转移方程就可以写出整个代码框架：

int maxProfit(int* prices, int pricesSize) {
    int sz = pricesSize;
    int i = 0;
    int dp[sz][2] = 0; //sz是最大买卖天数内的价格，2代表两种状态0和1
    dp[0][0] = 0,dp[0][1]=-prices[0];//设置边界值
    for(i=0;i<sz;i++)
    {
    dp[i][0] = fmax(dp[i-1][0] + dp[i][1]+prices[i]);
    dp[i][1] = fmax(dp[i-1][1] + dp[i-1][0]-prices[i]);//两种状态分别求最大利润
    }
    return [sz-1][0];
  }

优化

我们不难发现，我们的收益只和股票前一天的价格挂钩，和更早的状态没有关系，那我们为了减小时间复杂度和空间复杂度，可以将二维数组转化成一维滚动数组搞定

int maxProfit(int* prices, int pricesSize) {
    int dp[pricesSize][2];
    int dp0 = 0;dp1 = -prices[0];
    for (int i = 1; i < pricesSize; ++i)
     {
       int Dp0 = fmax(dp0, dp1+prices[i]);
        Dp1 = fmax(dp1, dp0-prices[i]); //同理转换出状态转移方程
    }
    dp0 = Dp0;
    dp1 = Dp1;//滚动更新dp0和dp1
    return dp[pricesSize - 1][0];
}

好了，今天就先到这里，摸了家人们，更多关于C语言动态规划点杀dp算法的资料请关注我们其它相关文章！