Java 细致图解带你分析汉诺塔

2024-12-19 22:48:34

一、汉诺塔问题来源

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘

二、问题分析

从简单问题开始

直接拿64个盘子来想，可能会比较难，我们可以先从1个盘子开始看，如下图：

一个盘子

A -> C

只有一个盘子情况下，我们可以直接将 A 柱子上面的盘子移到 C 柱子上

需要移动一次

两个盘子

当有两个盘子时，我们也可以通过下面方式实现：

A -> B A->C B->C

需要移动3次

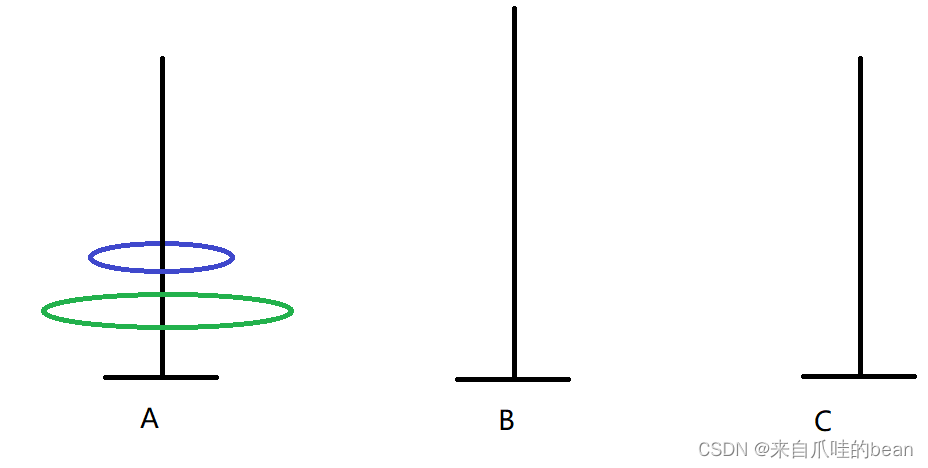
1. A -> B

2. A -> C

3. B -> C

三个盘子

当有三个盘子时，移动步骤如下：

A -> C A -> B C -> B A -> C B -> A B -> C A -> C

共需要移动7次

1. A -> C

2. A -> B

3. C -> B

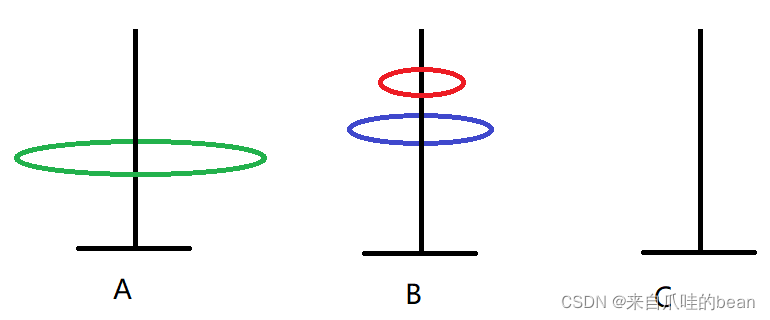
4. A -> C

5. B -> A

6. B -> C

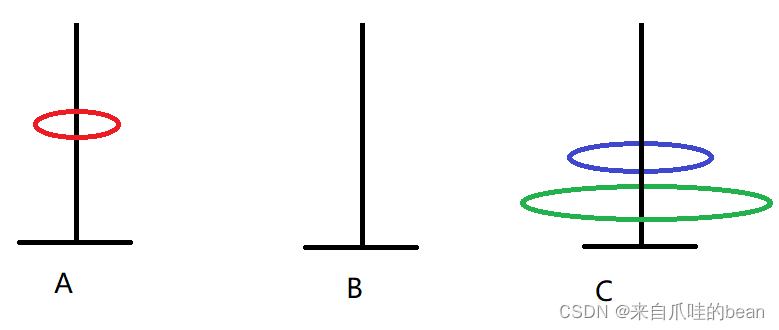
7. A -> C

这就完成了3个盘子的移动

当有 4 个盘子时，这个问题其实就已经很复杂了

规律推导

1个盘子移动1次

2个盘子移动3次

3个盘子移动7次

……

N 个盘子移动 2^N - 1 次

那么64个盘子就是需要移动 2^64 - 1 次

三、解决问题

我们可以通过递归来解决这个问题，获得正确的移动方式

如果有N个盘子该怎么移动呢？

整体思路

我们可以先将 N - 1 个盘子从 A 柱借助 C 柱移动到 B 柱，再将 A 柱剩下的一个盘子移动到 C柱，然后将 B 柱上的 N - 1 个盘子借助 A 柱移动到 C 柱，就完成了所有柱子的移动（中间具体移动过程暂不讨论）

上代码

public static void hanoi(int num, String src, String help, String dest) {
    if (num == 1) {     // 只有一个盘子的时候直接移动
        System.out.print(src + "->" + dest + "  ");  // 将一个盘子从源柱子挪到目标柱子
    } else {
        hanoi(num - 1, src, dest, help);   // 将n - 1个盘子从源柱子借助目标柱子挪到辅助柱子
        System.out.print(src + "->" + dest + "  ");  // 将一个盘子从源柱子挪到目标柱子
        hanoi(num - 1, help, src, dest);  // 将辅助柱子上n - 1个盘子借助源柱子挪到目标柱子
    }
}
public static void main(String[] args) {
    hanoi(3, "A", "B", "C");
}

这段代码中 src 是源柱子，help是辅助柱子，dest 是目标柱子

这是一个二路递归

运行结果：

这就成功完成了盘子的移动

四、婆罗门能否完成大梵天的任务

移动 64 个盘子需要多长时间

在这里我们假设婆罗门的人都非常聪明，不需要思考就直接能知道正确的移动方法，移动一个盘子需要一秒钟，一直不停的移

将2^64 - 1秒换算为年约为5849 4241 7355年（5849.42亿年），而地球存在至今不过45亿年，太阳系的预期寿命据说也就是数百亿年。真的过了5849.42亿年，不说太阳系和银河系，至少地球上的一切生命，连同梵塔、庙宇等，都早已经灰飞烟灭。

计算机移动64个盘子需要多长时间？

我的电脑核心频率为2.90GHz，也就是每秒钟运算 29 亿次，那么移动 2^64 - 1次需要的时间约为201年

到此这篇关于Java 细致图解带你分析汉诺塔的文章就介绍到这了,更多相关Java 汉诺塔内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

手把手带你用java搞定汉诺塔

目录什么是汉诺塔问题剖析 n=1 n=2 n=3 小结 Java代码实现代码讲解 move函数 hanoiTower函数附:C语言实现汉诺塔总结什么是汉诺塔汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移
Java 实现一个汉诺塔实战练习

汉诺塔简介: 我们想要实现的是让 A柱上的盘子,移动到C柱上 1层汉诺塔 2层汉诺塔 3层汉诺塔详解图第一步第二步第三步第四步第五步第六步第七步经过上面的图解,相比大家一定在一定程度了解到汉诺塔的游戏规则,以及怎么去玩. 总之最终C柱上第一个盘子,是最大,最顶的是最小的,而且在操作过程中,前几步就是为了让三个柱子中最大的盘子移动到C柱上, 然后不断,将它两个柱子中最大盘子往上累加,(盘子从大到小,从下往上摆放) 而且盘子一多,你就会发现过程中间,除了最大的盘子,其余的盘子都会
Java SE求解汉诺塔问题的示例代码

目录 1.问题描述 2.画图分析 3.问题讲解 4.代码实现 1.问题描述汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上. 并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘. 问应该如何操作? 2.画图分析一个圆盘的情况:移动前移动后 1个盘子:A直
Java 数据结构与算法系列精讲之汉诺塔

概述从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章. 汉诺塔汉诺塔 (Tower of Hanoi) 是一个源于印度的古老益智玩具. 汉诺塔由三根柱子和若干大小不同的圆盘组成. 目标是把圆盘从最左边的柱子移到最右边的柱子上. 如图: 递归递归 (Recursion) 指的是在函数中调用自身. 递归可以帮助我们简化问题, 使用更少的代码达成目标. 汉诺塔实现 public class 汉诺塔 { // 汉诺塔实现 private static void hanoi(i
Java手把手必会的实例汉诺塔讲解练习

最适合菜鸟的汉诺塔讲解问题引入汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘. 让我们先从小事入手. 标记汉诺塔的三根柱子分别为 a ,b ,c 标记汉诺塔上的圆盘分别为:1 ,2,3,4 -n a 柱上面只有一个圆盘时只有这一种走法 a柱上有两个圆盘时
Java递归来实现汉诺塔游戏,注释详细

我们很容易能想到,可以用递归来实现汉诺塔游戏.因为要将n(n>1)个盘子从"源"柱子移到"目标"柱子,我们要先把n-1个盘子从"源"柱子移到"辅助"柱子上,然后把最底下那一个盘子移到目标柱子上,最后把"辅助柱"上的n-1个盘子移动到目标柱子上.n==1时直接移到目标柱上,也是递归的出口. 有了以上思路的铺垫,就可以开始实现代码了. public class HanoiDemo { public sta
JAVA数据结构之汉诺塔代码实例

本文实例为大家分享了JAVA数据结构之汉诺塔的具体代码,供大家参考,具体内容如下 package p02.动态链表; import p01.动态数组.Stack; public class LinkedStack<E> implements Stack<E> { private LinkedList<E> list; public LinkedStack(){ list=new LinkedList<>(); } @Override public void
java递归实现汉诺塔步骤介绍

汉诺塔的规则是:一共三根柱子,一根柱子从上到下套着有小到大的若干个圆盘,要将所有圆盘按照这个排放顺序移动到第三根柱子上,并且每次只能移动一个圆盘. 可以将整个过程分为三个步骤来看: 第一步:将除最大圆盘外的n-1个圆盘移动辅助柱子上第二步:将最大的圆盘移动到目标柱子第三步:将n-1个圆盘从辅助柱子移动到目标柱子其中第一步又可以拆成一模一样的三步,可以看成一个n-1层的塔要移动到目标柱子,只不过目标柱子换了一个: 第三步也可以拆分成一模一样的三步: 多拆几次就会发现规律:第一步和第三步无论如
Java 细致图解带你分析汉诺塔

目录一.汉诺塔问题来源二.问题分析从简单问题开始三.解决问题整体思路四.婆罗门能否完成大梵天的任务移动 64 个盘子需要多长时间计算机移动64个盘子需要多长时间 ? 一.汉诺塔问题来源汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只
Java通过递归算法解决迷宫与汉诺塔及八皇后问题

目录 1.递归的重要规则 2.递归的三个案例 1.老鼠出迷宫 2.汉诺塔 3.八皇后 1.递归的重要规则在执行一个方法时,就创建一个新的受保护的独立空间(栈空间). 方法的局部变量时独立的,不会相互影响. 如果方法中使用的是应用类型变量(比如数组,对象),就会共享该引用类型的数据. 递归必须向退出递归的条件逼近,否则就是无限递归. 当一个方法执行完毕,或者遇到return,就会返回,遵循谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕. 2.递归的三个案例 1.老鼠出
Java编程用栈来求解汉诺塔问题的代码实例（非递归）

[题目] 汉诺塔问题比较经典,这里修改一下游戏规则:现在限制不能从最左侧的塔直接移动到最右侧,也不能从最右侧直接移动到最左侧,而是必须经过中间.求当塔有N层的时候,打印最优移动过程和最优移动总步数. [解答] 上一篇用的是递归的方法解决这个问题,这里我们用栈来模拟汉诺塔的三个塔,也就是不用递归的方法原理是这样的:修改后的汉诺塔问题不能让任何塔从左直接移动到右,也不能从右直接移动到左,而是要经过中间,也就是说,实际上能做的动作,只有四个:左->中,中->左,中->右,右->中用栈
Java数据结构及算法实例：汉诺塔问题 Hanoi

/** * 汉诺塔大学的时候就学过,但是根本没搞明白,唯一知道的就是要用递归的方法来求解. * 问题描述: * 有三根杆子A,B,C.A杆上有N个(N>1)穿孔圆盘,盘的尺寸由下到上依次变小. * 要求按下列规则将所有圆盘移至C杆: * 1.每次只能移动一个圆盘: * 2.大盘不能叠在小盘上面. * 提示:可将圆盘临时置于B杆,也可将从A杆移出的圆盘重新移回A杆, * 但都必须尊循上述两条规则. * 问:如何移?最少要移动多少次? * 解决方法: * 假设只有2个盘子,柱子分别是A, B, C柱
java数据结构和算法学习之汉诺塔示例

复制代码代码如下: package com.tiantian.algorithms;/** * _|_1 | | * __|__2 | | * ___|___3 | | (1).把A上的4个木块移动到C上. * ____|____4 | | *
java 实现汉诺塔详解及实现代码

java 实现汉诺塔详解及实现代码汉诺塔问题:有三根柱子A,B,C,其中A上面有n个圆盘,从上至下圆盘逐渐增大,每次只能移动一个圆盘,并且规定大的圆盘不能叠放在小的圆盘上面,现在想要把A上面的n个圆盘全部都移动到C上面,输出移动的总步数以及移动的过程分析: //先求出移动的总步数 1,假设g(n)表示n个圆盘时的移动总的步数,当n=1时,g(1)=1; 2.现在可以把g(n)进行细分为三步: 1>先将n-1个圆盘从A通过C移动到B上面,相当于将n-1个圆盘从A移动到C,因此需要g(n-1)步
带你理解C语言中的汉诺塔公式

目录汉诺塔公式汉诺塔问题在数学层面的公式: C语言递归公式两层汉诺塔三层汉诺塔总结汉诺塔公式汉诺塔问题在数学层面的公式: 不用说,你看到这个公式一定一脸懵逼,我现在来讲解这个公式的作用. 先来回想一下大象放冰箱要几步,三步吧,打开冰箱,放进去,关上门就行了,我们先不要去思考一些细碎的步骤,将一个复杂的问题先简单化,再慢慢去分析. 那汉诺塔问题也是同样的简单三步:(假设有n个盘子) 一.把最大的盘子留在A柱,然后将其他的盘子全放在B柱. 二.把最大的盘子放到C柱. 三.然后将B柱上的