超详细解析C++实现归并排序算法

目录

• 一、前言
• 分治算法
• 分治算法解题方法
• 二、归并排序
• 1.问题分析
• 2.算法设计
• 3.算法分析
• 三、AC代码

一、前言

分治算法

归并排序，其实就是一种分治算法 ，那么在了解归并排序之前，我们先来看看什么是分治算法。在算法设计中，我们引入分而治之的策略，称为分治算法，其本质就是将一个大规模的问题分解为若干个规模较小的相同子问题，分而治之。

分治算法解题方法

1.分解：

将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。

2.治理：

求解各个子问题。由于各个子问题与原问题形式相同，只是规模较小而已，而当子问题划分得足够小时，就可以用简单的方法解决。

3.合并

按原问题的要求，将子问题的解逐层合并构成原问题的解。

二、归并排序

1.问题分析

归并排序是比较稳定的排序方法。它的基本思想是把待排序的元素分解成两个规模大致相等的子序列。如果不易分解，将得到的子序列继续分解，直到子序列中包含的元素个数为1。因为单个元素的序列本身就是有序的，此时便可以进行合并，从而得到一个完整的有序序列。

2.算法设计

（1）分解：

将待排序的元素分成大小大致一样的两个子序列。

（2）治理：

对两个子序列进行个并排序。

（3）合并：

将排好序的有序子序列进行合并，得到最终的有序序列。

3.算法分析

首先我们先给定一个无序的数列（42，15，20，6，8，38，50，12），我们进行合并排序数列，如下图流程图所示：

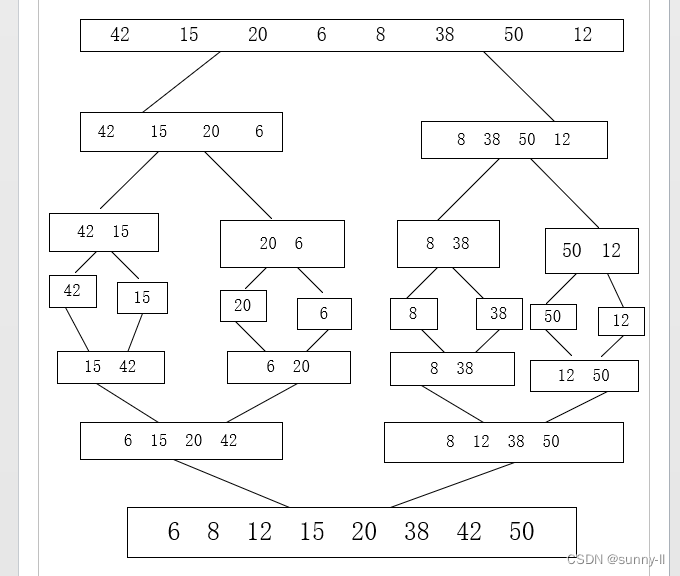
步骤一：首先将待排序的元素分成大小大致相同的两个序列。

步骤二：再把子序列分成大小大致相同的两个子序列。

步骤三：如此下去，直到分解成一个元素停止，这时含有一个元素的子序列都是有序的。

步骤四：进行合并操作，将两个有序的子序列合并为一个有序序列，如此下去，直到所有的元素都合并为一个有序序列。

举例，下面我将以序列（4，9，15，24，30，2，6，18，20）进行图解。

（1）初始化：i = low，j = mid+1，mid = (low+hight)/2 ，申请一个辅助数组 b

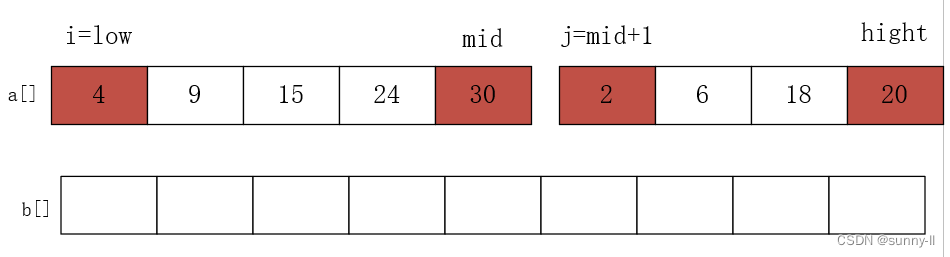
int* b = new int[hight - low + 1];  //用 new 申请一个辅助函数
	int i = low, j = mid + 1, k = 0;    // k为 b 数组的小标

（2）现在比较 a [i]  和 b[j]  ，将较小的元素放在 b 数组中，相应的指针向后移动，直到 i > mid 或者 j>hight 时结束。

while (i <= mid && j <= hight)
 {
	if (a[i] <= a[j])
	{
		b[k++] = a[i++];  //按从小到大存放在 b 数组里面
	}
	else
	{
		b[k++] = a[j++];
	}
  }

进行第一次比较 a[i]=4  和 a[j]=2，将较小的元素 2 放入数组  b  中，j++,k++，如下图：

进行第二次比较 a[i]=4  和 a[j]=6，将较小的元素放 4 入数组  b  中，i++,k++，如下图：

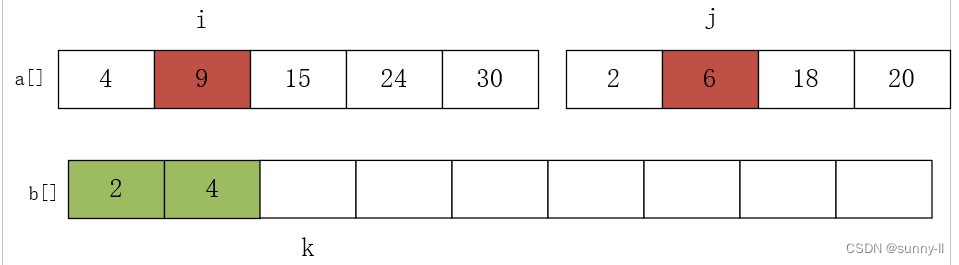
进行第三次比较 a[i]=9  和 a[j]=6，将较小的元素放 6 入数组  b  中，j++,k++，如下图：

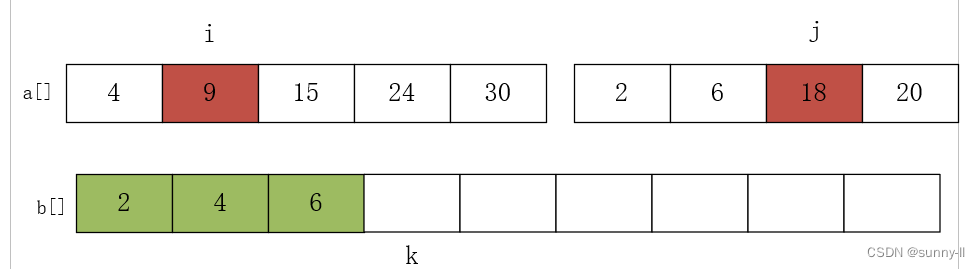
进行第四次比较 a[i]=9  和 a[j]=18，将较小的元素放 9 入数组  b  中，i++,k++，如下图：

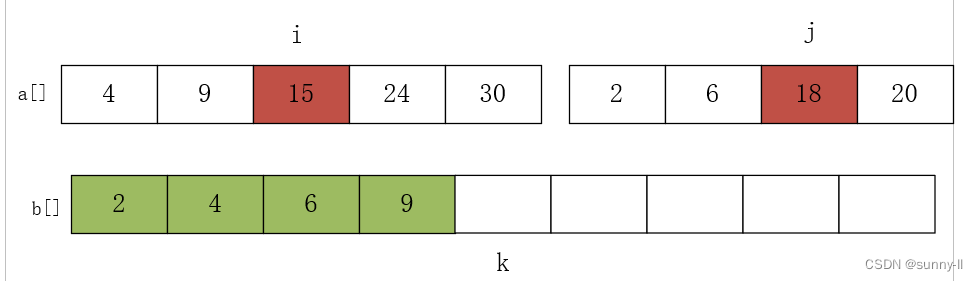
进行第五次比较 a[i]=15  和 a[j]=18，将较小的元素放 15 入数组  b  中，i++,k++，如下图：

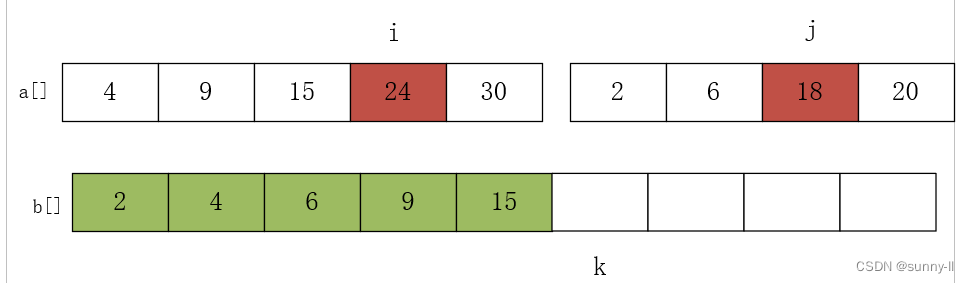
进行第六次比较 a[i]=24  和 a[j]=18，将较小的元素放 18 入数组  b  中，j++,k++，如下图：

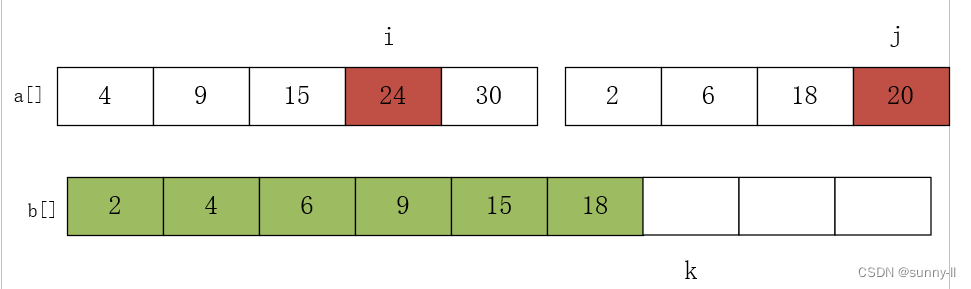
进行第七次比较 a[i]=24  和 a[j]=20，将较小的元素放 20 入数组  b  中，j++,k++，如下图：

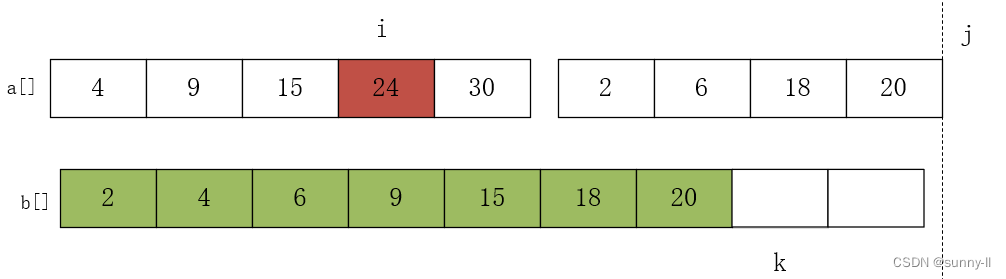
此时，j>hight 了，while循环结束，但 a 数组还剩下元素（i<mid）可直接放入  b  数组就可以了。如下图所示：

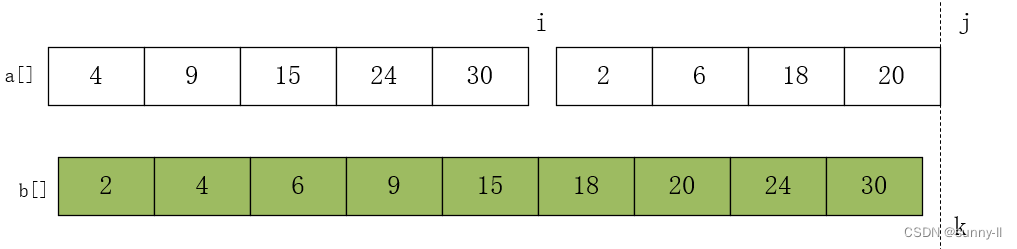
while (i <= mid)  // j 序列结束，将剩余的 i 序列补充在 b 数组中
	{
		b[k++] = a[i++];
	}
	while (j <= hight)// i 序列结束，将剩余的 j 序列补充在 b 数组中
	{
		b[k++] = a[j++];
	}

现在将  b  数组的元素赋值给 a 数组，再将 b  数组销毁，即可。

for (int i = low; i <= hight; i++)  //将 b 数组的值传递给数组 a
	{
		a[i] = b[k++];
	}
	delete[]b;     // 辅助数组用完后，将其的空间进行释放（销毁）

（3）递归的形式进行归并排序

void mergesort(int* a, int low, int hight) //归并排序
{
	if (low < hight)
	{
		int mid = (low + hight) / 2;
		mergesort(a, low, mid);          //对 a[low,mid]进行排序
		mergesort(a, mid + 1, hight);    //对 a[mid+1,hight]进行排序
		merge(a, low, mid, hight);       //进行合并操作
	}
}

三、AC代码

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
void merge(int* a, int low, int mid, int hight)  //合并函数
{
	int* b = new int[hight - low + 1];  //用 new 申请一个辅助函数
	int i = low, j = mid + 1, k = 0;    // k为 b 数组的小标
	while (i <= mid && j <= hight)
	{
		if (a[i] <= a[j])
		{
			b[k++] = a[i++];  //按从小到大存放在 b 数组里面
		}
		else
		{
			b[k++] = a[j++];
		}
	}
	while (i <= mid)  // j 序列结束，将剩余的 i 序列补充在 b 数组中
	{
		b[k++] = a[i++];
	}
	while (j <= hight)// i 序列结束，将剩余的 j 序列补充在 b 数组中
	{
		b[k++] = a[j++];
	}
	k = 0;  //从小标为 0 开始传送
	for (int i = low; i <= hight; i++)  //将 b 数组的值传递给数组 a
	{
		a[i] = b[k++];
	}
	delete[]b;     // 辅助数组用完后，将其的空间进行释放（销毁）
}
void mergesort(int* a, int low, int hight) //归并排序
{
	if (low < hight)
	{
		int mid = (low + hight) / 2;
		mergesort(a, low, mid);          //对 a[low,mid]进行排序
		mergesort(a, mid + 1, hight);    //对 a[mid+1,hight]进行排序
		merge(a, low, mid, hight);       //进行合并操作
	}
}
int main()
{
	int n, a[100];
	cout << "请输入数列中的元素个数 n 为：" << endl;
	cin >> n;
	cout << "请依次输入数列中的元素：" << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	mergesort(a, 0, n-1);
	cout << "归并排序结果" << endl;
	for (int i = 0; i < n; i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
	return 0;
}

以上就是超详细解析C++实现归并排序算法的详细内容，更多关于C++归并排序算法的资料请关注我们其它相关文章！