python scipy求解非线性方程的方法(fsolve/root)

使用scipy.optimize模块的root和fsolve函数进行数值求解线性及非线性方程，下面直接贴上代码，代码很简单

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root,fsolve
#plt.rc('text', usetex=True) #使用latex
## 使用scipy.optimize模块的root和fsolve函数进行数值求解方程

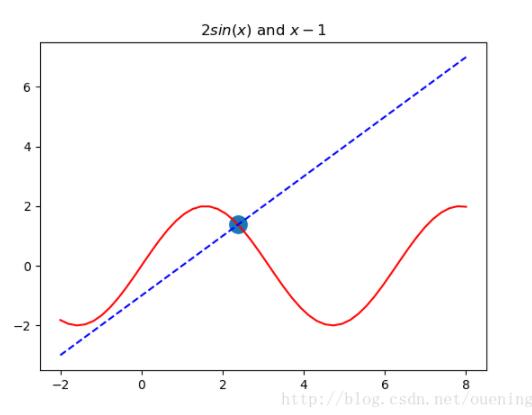
## 1、求解f(x)=2*sin(x)-x+1
rangex1 = np.linspace(-2,8)
rangey1_1,rangey1_2 = 2*np.sin(rangex1),rangex1-1
plt.figure(1)
plt.plot(rangex1,rangey1_1,'r',rangex1,rangey1_2,'b--')
plt.title('$2sin(x)$ and $x-1$')

def f1(x):
 return np.sin(x)*2-x+1

sol1_root = root(f1,[2])
sol1_fsolve = fsolve(f1,[2])
plt.scatter(sol1_fsolve,2*np.sin(sol1_fsolve),linewidths=9)
plt.show()

## 2、求解线性方程组{3X1+2X2=3;X1-2X2=5}
def f2(x):
 return np.array([3*x[0]+2*x[1]-3,x[0]-2*x[1]-5])

sol2_root = root(f2,[0,0])
sol2_fsolve = fsolve(f2,[0,0])
print(sol2_fsolve) # [2. -1.5]

a = np.array([[3,2],[1,-2]])
b = np.array([3,5])
x = np.linalg.solve(a,b)
print(x) # [2. -1.5]
## 3、求解非线性方程组
def f3(x):
 return np.array([2*x[0]**2+3*x[1]-3*x[2]**3-7,
     x[0]+4*x[1]**2+8*x[2]-10,
     x[0]-2*x[1]**3-2*x[2]**2+1])

sol3_root = root(f3,[0,0,0])
sol3_fsolve = fsolve(f3,[0,0,0])
print(sol3_fsolve)

## 4、非线性方程
def f4(x):
 return np.array(np.sin(2*x-np.pi)*np.exp(-x/5)-np.sin(x))
init_guess =np.array([[0],[3],[6],[9]])
sol4_root = root(f4,init_guess)
sol4_fsolve = fsolve(f4,init_guess)
print(sol4_fsolve)
t = np.linspace(-2,12,2000)
y1 = np.sin(2*t-np.pi)*np.exp(-t/5)
y2 = np.sin(t)
plt.figure(2)
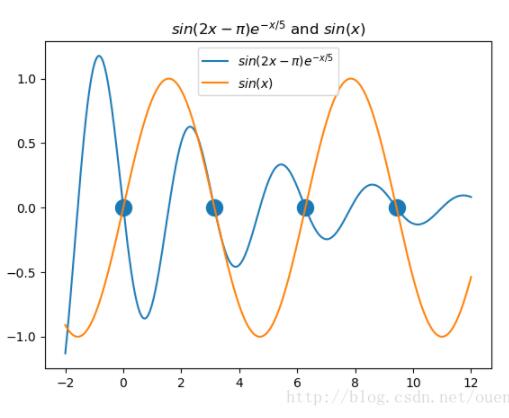
a , = plt.plot(t,y1,label='$sin(2x-\pi)e^{-x/5}$')
b , = plt.plot(t,y2,label='$sin(x)$')
plt.scatter(sol4_fsolve,np.sin(sol4_fsolve),linewidths=8)
plt.title('$sin(2x-\pi)e^{-x/5}$ and $sin(x)$')
plt.legend()

以上这篇python scipy求解非线性方程的方法(fsolve/root)就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python基于高斯消元法计算线性方程组示例

    本文实例讲述了Python基于高斯消元法计算线性方程组.分享给大家供大家参考,具体如下: #!/usr/bin/env python # coding=utf-8 # 以上的信息随自己的需要改动吧 def print_matrix( info, m ): # 输出矩阵 i = 0; j = 0; l = len(m) print info for i in range( 0, len( m ) ): for j in range( 0, len( m[i] ) ): if( j == l ):

  • python用fsolve、leastsq对非线性方程组求解

    背景: 实现用python的optimize库的fsolve对非线性方程组进行求解.可以看到这一个问题实际上还是一个优化问题,也可以用之前拟合函数的leastsq求解.下面用这两个方法进行对比: 代码: from scipy.optimize import fsolve,leastsq from math import sin,cos def f(x): x0 = float(x[0]) x1 = float(x[1]) x2 = float(x[2]) return [ 5*x1+3, 4*x

  • python计算方程式根的方法

    本文实例讲述了python计算方程式根的方法.分享给大家供大家参考.具体实现方法如下: ''' roots = polyRoots(a). Uses Laguerre's method to compute all the roots of a[0] + a[1]*x + a[2]*x^2 +...+ a[n]*x^n = 0. The roots are returned in the array 'roots', ''' from evalPoly import * from numpy i

  • python/sympy求解矩阵方程的方法

    sympy版本:1.2 假设求解矩阵方程 AX=A+2X 其中 求解之前对矩阵方程化简为 (A−2E)X=A 令 B=(A−2E) 使用qtconsole输入下面程序进行求解 In [26]: from sympy import * In [27]: from sympy.abc import * In [28]: A=Matrix([[4,2,3],[1,1,0],[-1,2,3]]) In [29]: A Out[29]: Matrix([ [ 4, 2, 3], [ 1, 1, 0], [

  • Python线性方程组求解运算示例

    Python线性方程组求解运算示例

    本文实例讲述了Python线性方程组求解运算.分享给大家供大家参考,具体如下: 求解线性方程组比较简单,只需要用到一个函数(scipy.linalg.solve)就可以了.比如我们要求以下方程的解,这是一个非齐次线性方程组: 3x_1 + x_2 - 2x_3 = 5 x_1 - x_2 + 4x_3 = -2 2x_1 + 3x_3 = 2.5 代码如下: # coding=utf-8 import numpy as np from scipy.linalg import solve a =

  • 基于python解线性矩阵方程(numpy中的matrix类)

    这学期有一门运筹学,讲的两大块儿:线性优化和非线性优化问题.在非线性优化问题这里涉及到拉格朗日乘子法,经常要算一些非常变态的线性方程,于是我就想用python求解线性方程.查阅资料的过程中找到了一个极其简单的解决方式,也学到了不少东西.先把代码给出. import numpy as np # A = np.mat('1 2 3;2 -1 1;3 0 -1') A = np.array([[1, 2, 3], [2, -1, 1], [3, 0, -1]]) b = np.array([9, 8,

  • Python编程实现数学运算求一元二次方程的实根算法示例

    Python编程实现数学运算求一元二次方程的实根算法示例

    本文实例讲述了Python编程实现数学运算求一元二次方程的实根算法.分享给大家供大家参考,具体如下: 问题: 请定义一个函数quadratic(a, b, c),接收3个参数,返回一元二次方程:ax² + bx + c = 0的两个解. 实现代码: #!/usr/bin/env python # -*- coding: utf-8 -*- import math def quadratic(a,b,c): if a == 0: raise TypeError('a不能为0') if not is

  • Python实现求解一元二次方程的方法示例

    本文实例讲述了Python实现求解一元二次方程的方法.分享给大家供大家参考,具体如下: 1. 引入math包 2. 定义返回的对象 3. 判断b*b-4ac的大小 具体计算代码如下: # -*- coding:utf-8 -*- #! python2 import math class Result: result1 = 0 result2 = 0 def __init__(self, r1, r2): self.result1 = r1 self.result2 = r2 def __retu

  • python scipy求解非线性方程的方法(fsolve/root)

    使用scipy.optimize模块的root和fsolve函数进行数值求解线性及非线性方程,下面直接贴上代码,代码很简单 from scipy.integrate import odeint import numpy as np import matplotlib.pyplot as plt from scipy.optimize import root,fsolve #plt.rc('text', usetex=True) #使用latex ## 使用scipy.optimize模块的roo

  • Python使用scipy进行曲线拟合的方法实例

    Python使用scipy进行曲线拟合的方法实例

    目录 导读 曲线拟合 总结 导读 曲线拟合的应用在生活中随处可见,不知道大家是否还记得物理实验中的自由落体运动中下降高度与时间关系之间的探究,在初速度为0的情况下,我们想要探究下降高度与时间的关系. 我们当时采用的方法是通过设置不同的下降时间来记录下降的高度,测量记录多组数据之后,再利用二维坐标系将记录的点绘制到坐标系当中去,然后保证绘制的曲线到这些点的距离之和最小,最终得到的曲线就是h与t的关系. 绘制出h和t的关系之后,我就可以知道任意取值t在初速度为0的情况下,下降高度h对应的值.除此之外

  • python使用分治法实现求解最大值的方法

    本文实例讲述了python使用分治法实现求解最大值的方法.分享给大家供大家参考.具体分析如下: 题目: 给定一个顺序表,编写一个求出其最大值和最小值的分治算法. 分析: 由于顺序表的结构没有给出,作为演示分治法这里从简顺序表取一整形数组数组大小由用户定义,数据随机生成.我们知道如果数组大小为 1 则可以直接给出结果,如果大小为 2则一次比较即可得出结果,于是我们找到求解该问题的子问题即: 数组大小 <= 2.到此我们就可以进行分治运算了,只要求解的问题数组长度比 2 大就继续分治,否则求解子问题

  • Python求解平方根的方法

    本文实例讲述了Python求解平方根的方法.分享给大家供大家参考.具体如下: 主要通过SICP的内容改写而来.基于newton method求解平方根.代码如下: #!/usr/bin/python def sqrt_iter(guess,x): if(good_enough(guess, x)): print guess else: sqrt_iter(improve(guess, x),x) def improve(guess, x): return average(guess, x/gue

  • Python实现求解括号匹配问题的方法

    Python实现求解括号匹配问题的方法

    本文实例讲述了Python实现求解括号匹配问题的方法.分享给大家供大家参考,具体如下: 这个在本科学习数据结构的时候已经接触很多了,主流的思想是借助栈的压入.弹出来进行匹配,至于python的话可以使用列表来完成这个操作,因为列表的append方法相当于栈的push方法,列表的pop方法相当于栈的pop方法. 主要的思路: 首先设置两个列表分别存放的是各种括号的开括号和闭括号,然后遍历给定的字符串,分如下几种情况: 1.字符串首字符出现在闭括号列表中,直接结束,输出错误 2.字符串长度不为偶数,

  • python 实现求解字符串集的最长公共前缀方法

    问题比较简单,给定一个字符串集合求解其中最长的公共前缀即可,这样的问题有点类似于最长公共子序列的问题,但是比求解最长最长公共子序列简单很多,因为是公共前缀,这样的话只需要挨个遍历即可,只要遍历长度结束或者结束前发现有不相同的即可终止,返回不同位置之前的子序列即可,下面是具体的实现: #!usr/bin/env python #encoding:utf-8 ''' __Author__:沂水寒城 功能:求解字符串集的最长公共前缀 ''' def find_longest_prefix(str_li

  • Python实现求解最大公约数的五种方法总结

    目录 方法一:短除法 方法二:欧几里得算法(辗转相除法) 方法三:更相减损术 方法四:穷举法(枚举法) 方法五:Stein算法 求最大公约数是习题中比较常见的类型,下面小编会给大家提供五种比较常见的算法,记得帮忙点个赞哦! 一般来说,最大公约数的求法大概有5种 方法一:短除法 短除法是求最大公因数的一种方法,也可用来求最小公倍数.求几个数最大公因数的方法,开始时用观察比较的方法,即:先把每个数的因数找出来,然后再找出公因数,最后在公因数中找出最大公因数.后来,使用分解质因数法来分别分解两个数的因

随机推荐