python中树与树的表示知识点总结
一、什么是树
客观世界中许多事物存在层次关系
人类社会家谱社会组织结构图书信息管理
其中,人类社会家谱如下图所示:

通过上述所说的分层次组织,能够使我们在数据的管理上有更高的效率!那么,对于数据管理的基本操作——查找,我们如何实现有效率的查找呢?
二、查找
查找:根据某个给定关键字K,从集合R中找出关键字与K相同的记录
静态查找:集合中记录是固定的,即对集合的操作没有插入和删除,只有查找
动态查找:集合中记录是动态变化的,即对集合的操作既有查找,还可能发生插入和删除(动态查找不在我们考虑范围内)
2.1 静态查找 2.1.1 方法1:顺序查找
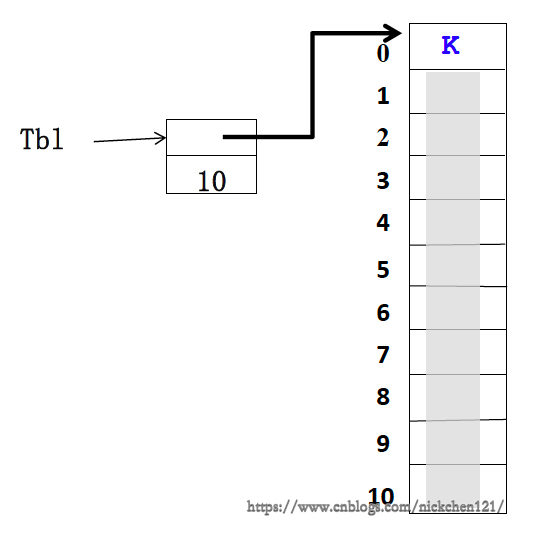
/* c语言实现 */
int SequentialSearch (StaticTable *Tbl, ElementType K)
{
// 在表Tbl[1]~Tb1[n]中查找关键字为K的数据元素
int i;
Tbl->Element[0] = K; // 建立哨兵,即没找到可以返回哨兵的索引0表示未找到
for (i = Tbl->Length; Tbl->Element[i] != K; i--); // 查找成功返回所在单元下标;不成功放回0
return i;
}
顺序查找算法的时间复杂度为O(n)
2.1.2 方法2:二分查找(Binary Search)
假设n个数据元素的关键字满足有序(比如:小到大),即\(k_1<k_2<\cdots<k_n\),并且是连续存放(数组),那么可以进行二分查找。
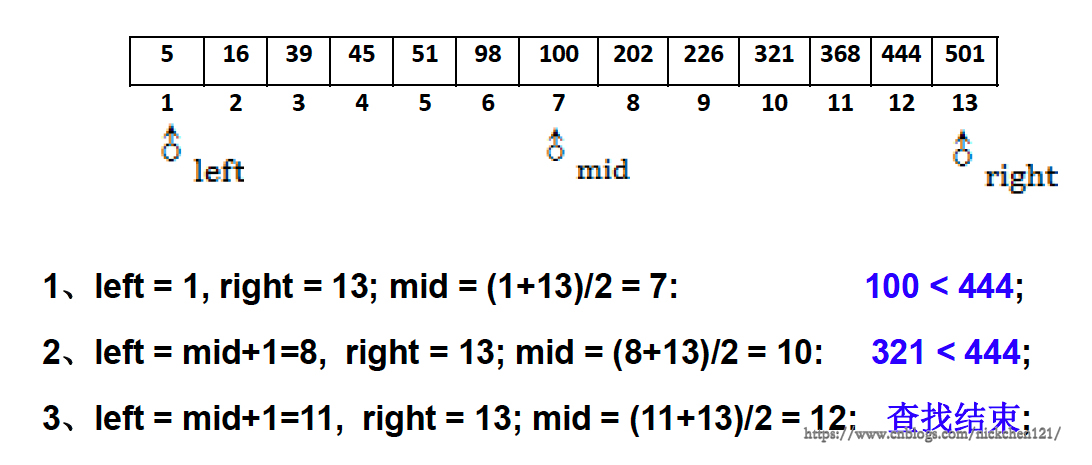
例:假设有13个数据元素,按关键字由小到大顺序存放。二分查找关键字为444的数据元素过程如下图:
仍然以上面13个数据元素构成的有序线性表为例,二分查找关键字为43的数据元素如下图:

/* c语言实现 */
int BinarySearch (StaticTable *Tbl, ElementType K)
{
// 在表中Tbl中查找关键字为K的数据元素
int left, right, mid, NoFound = -1;
left = 1; // 初始左边界
right = Tbl->Length; // 初始右边界
while (left <= right)
{
mid = (left + right) / 2; // 计算中间元素坐标
if (K < Tbl->Element[mid]) right = mid - 1; // 调整右边界
else if (K > Tbl->Element[mid]) left = mid + 1; // 调整左边界
else return mid; // 查找成功,返回数据元素的下标
}
return NotFound; // 查找不成功,返回-1
}
# python语言实现
def binary_chop(alist, data):
n = len(alist)
first = 0
last = n - 1
while first <= last:
mid = (last + first) // 2
if alist[mid] > data:
last = mid - 1
elif alist[mid] < data:
first = mid + 1
else:
return True
return False
二分查找算法具有对数的时间复杂度O(logN)
二分查找算法虽然解决了查找的时间复杂度问题,但是对于数据的插入和删除确是O(n)的,因此有没有一种数据结构,既可以减少数据查找的时间复杂度,又可以减少数据的插入和删除的复杂度呢?
三、二分查找判定树
除了使用上述两个方法进行关键字的查找,我们还可以通过二叉树这种数据结构完成关键字的查找。
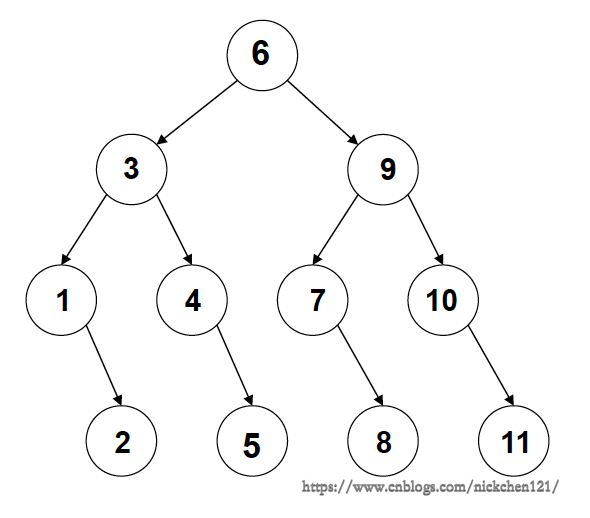
从上图可以看出,如果我们需要寻找数字8,可以通过以下4步实现(可能看不懂,未来会看得懂):
根节点6小于8,往6的右子节点9找结点9大于8,往9的左子结点7找结点7小于8,往7的左子结点找找到8 判定树上每个结点需要的查找次数刚好为该结点所在的层数;查找成功时查找次数不会超过判定树的深度 N个结点的判定树的深度为\([log_2{n}]+1\) \(ASL = (4*4+4*3+2*2+1)/11 = 3\) 四、树的定义
树(Tree):\(n(n\geq{0})\)个结点构成的有限集合。
当n=0时,称为空树对于任一颗非空树(n>0),它具备以下性质: 树中有一个称为根(Root)的特殊结点,用r表示其余结点可分为m(m>0)个互不相交的有限集\(T_1,T_2,\cdots,T_m\),其中每个集合本身又是一棵树,称为原来树的子树(SubTree)
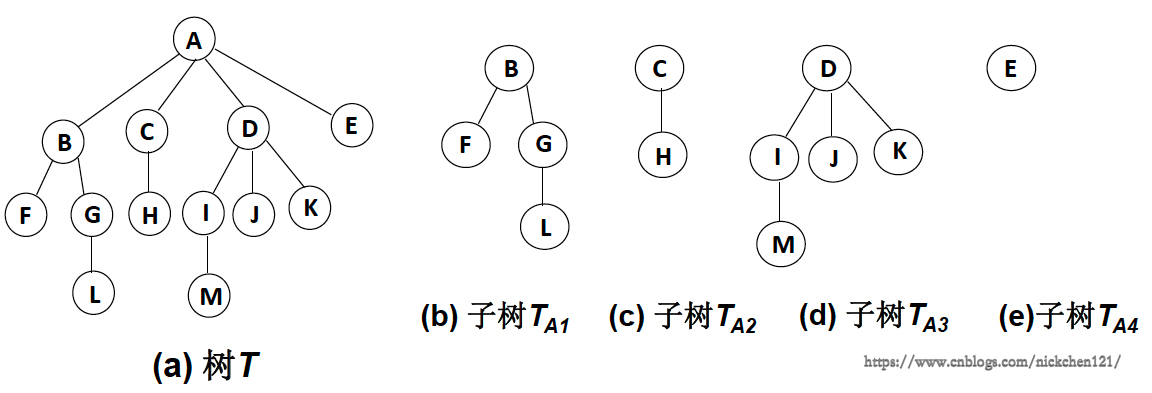
五、树与非树
牢记树有以下3个特性:
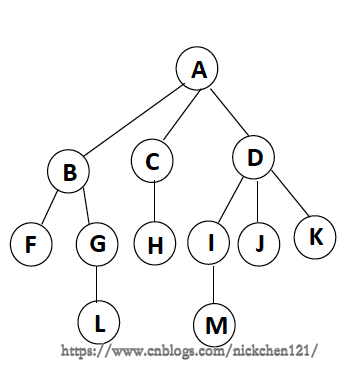
子树是不相交的;除了根结点外,每个结点有且仅有一个父结点;一颗N个结点的树有N-1条边 5.1 非树

5.2 树
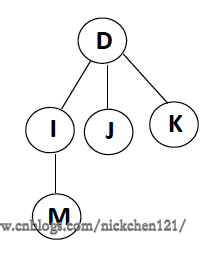
六、树的一些基本术语
结点的度(Degree):结点的子树个数树的度:树的所有结点中最大的度数叶结点(Leaf): 度为0的结点父结点(Parent):有子树的结点是其子树的根结点的父结点子结点(Child):若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子结点
兄弟结点(Sibling):具有同一父结点的各结点彼此是兄弟结点
路径和路径长度:从结点\(n_1\)到\(n_k\)的路径为一个结点序列\(n_1 , n_2 ,\cdots, n_k\) , \(n_i\)是\(n_{i+1}\)的父结点。路径所包含边的个数为路径的长度
祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点
子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙
结点的层次(Level):规定根结点在1层,其它任一结点的层数是其父结点的层数加1
树的深度(Depth):树中所有结点中的最大层次是这棵树的深度
七、树的表示
7.1 树的链表表示
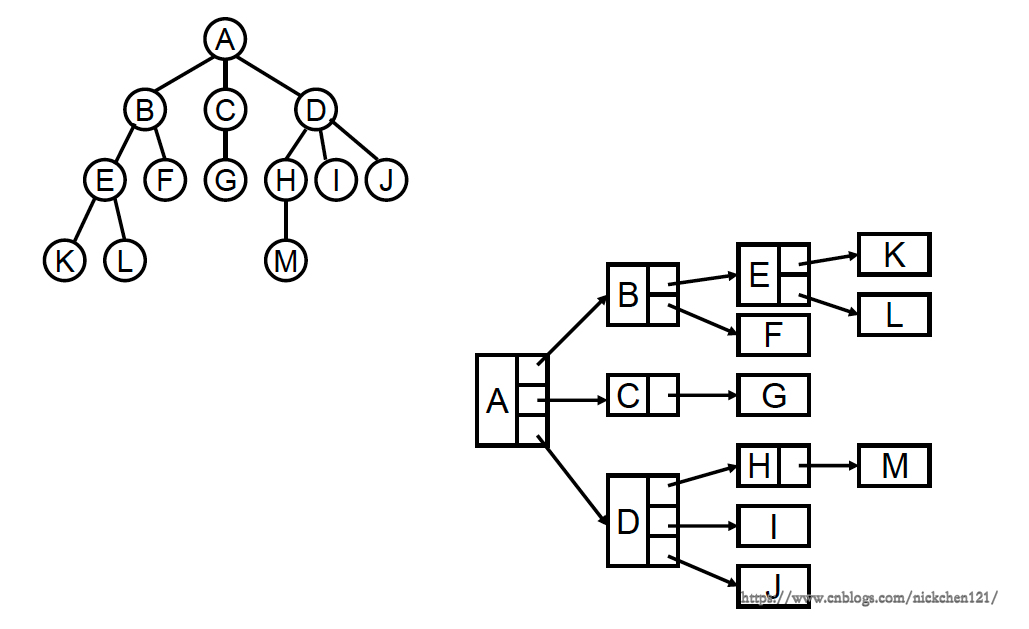
上图所示树的链表表示法有很大的缺陷,假设树的深度非常大,并且不能保证所有树的子结点都有3个,那么会造成很大程度的浪费。
7.2 树的链表(儿子-兄弟)表示法
为了解决树的普通链表表示会有空间的浪费的缺陷,我们可以把链表的指针设置两个链接,一个链接指向儿子结点,另一个链接指向兄弟结点,如下图所示:
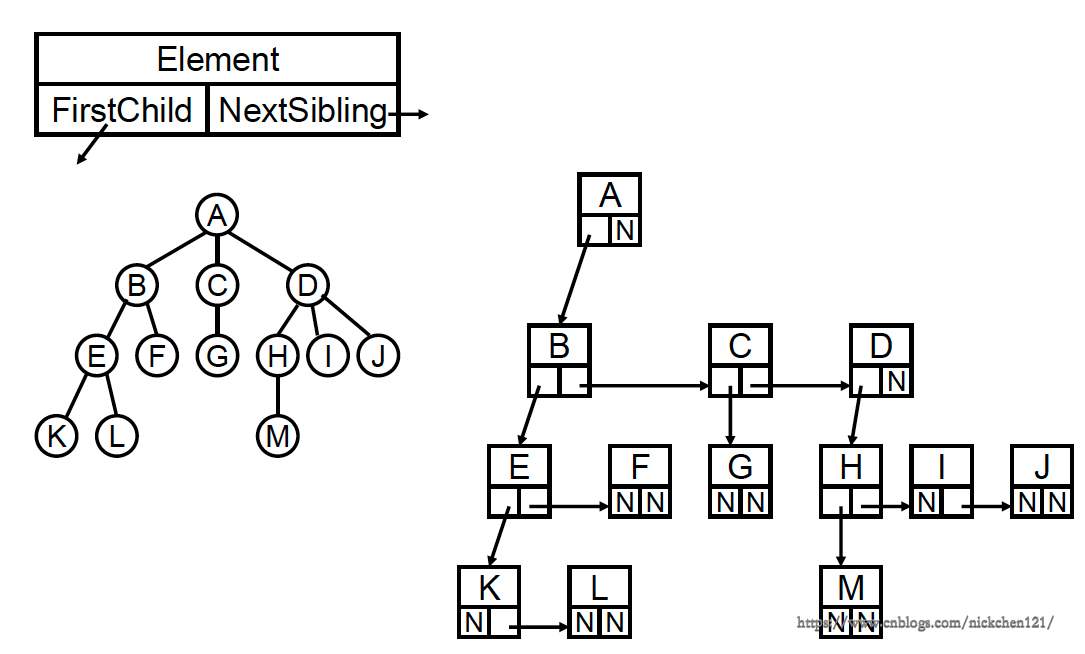
上图所示的树的表示方法,已经足够完美了,但是如果我们把链表表示的树旋转45°角,会发现如下图所示:
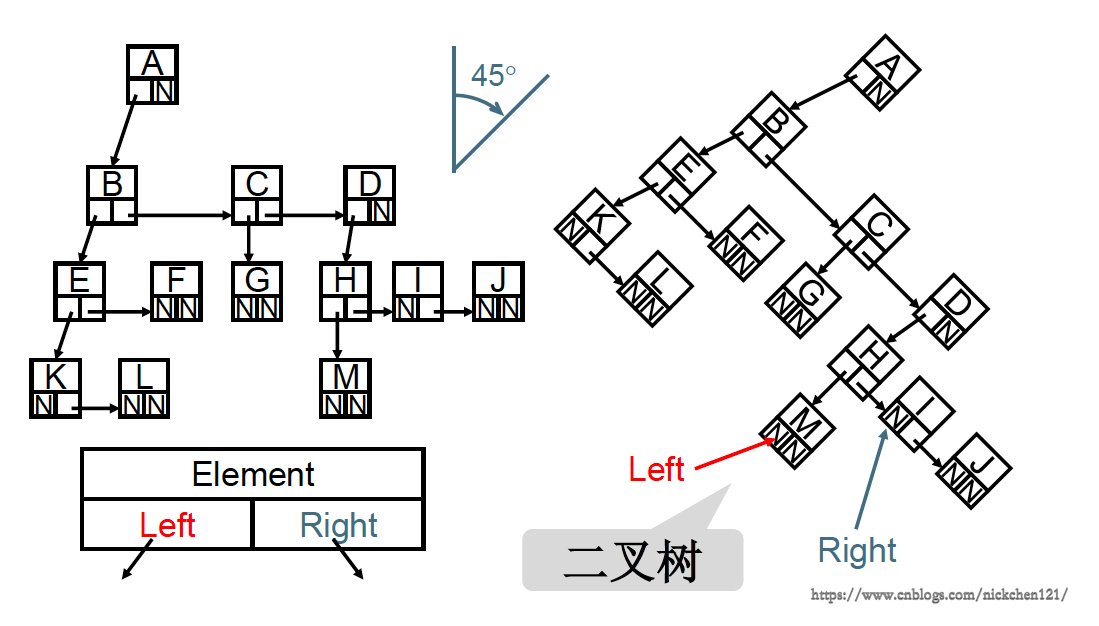
经过45°角的旋转,我们会发现一颗二叉树(一个结点至多拥有2个子结点的树),也就是说最普通的树其实可以通过二叉树表示,也就是说我们只要把二叉树研究透了,我们即研究透了树。
以上就是本次全部相关知识点内容,感谢大家的阅读和对我们的支持。
