基于Matlab实现离散系统分岔图的绘制

目录

• 1.一维离散分岔图
• 2.二维离散分岔图
• 3.封面图绘制

1.一维离散分岔图

一维那非常简单哈，就循环着画呗，以下举两个简单的例子 ：

% x(n+1)=1-r*x(n)^2
% (r∈(0,2),x∈[-1,1])的分支混沌图。
hold on

f=@(x,r)1-r.*x.^2;
r=0:.01:2;
x=0; % x初值

for n=1:1000
    x=f(x,r);
    if n>100 % 稳定后开始绘图
        plot(r,x,'k.','MarkerSize',1);
        drawnow
    end
end

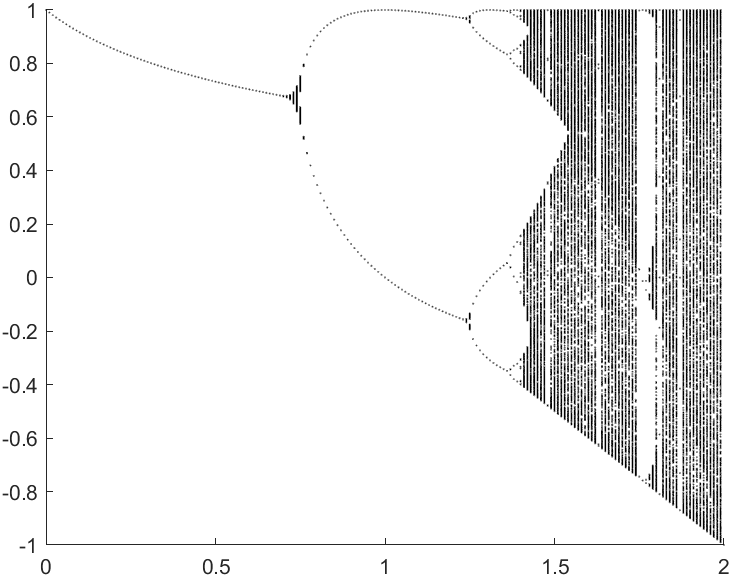
% Logistic系统
% x(n+1)=r*x(n)-r*x(n)^2
% (r∈(2.6,4),x∈(0,1])的分支混沌图。
hold on

f=@(x,r)r.*x-r.*x.^2;
r=2.6:.01:4;
x=0.6; % x初值

for n=1:1000
    x=f(x,r);
    if n>100 % 稳定后开始绘图
        plot(r,x,'k.','MarkerSize',1);
        drawnow
    end
end

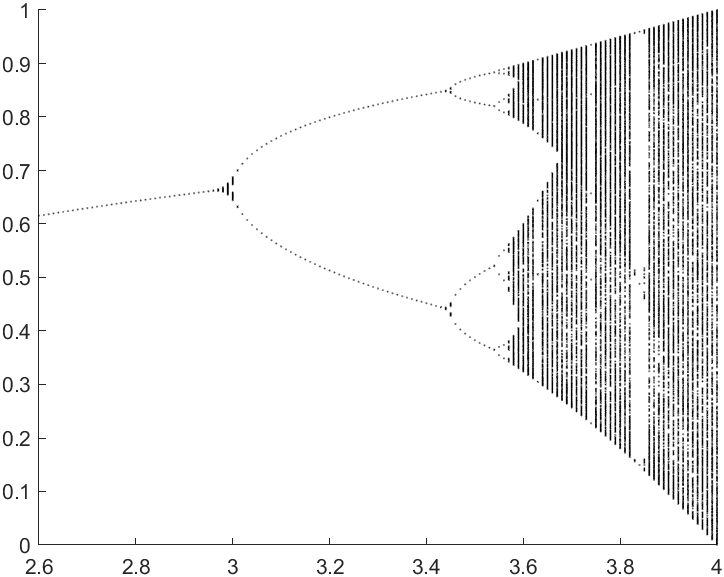
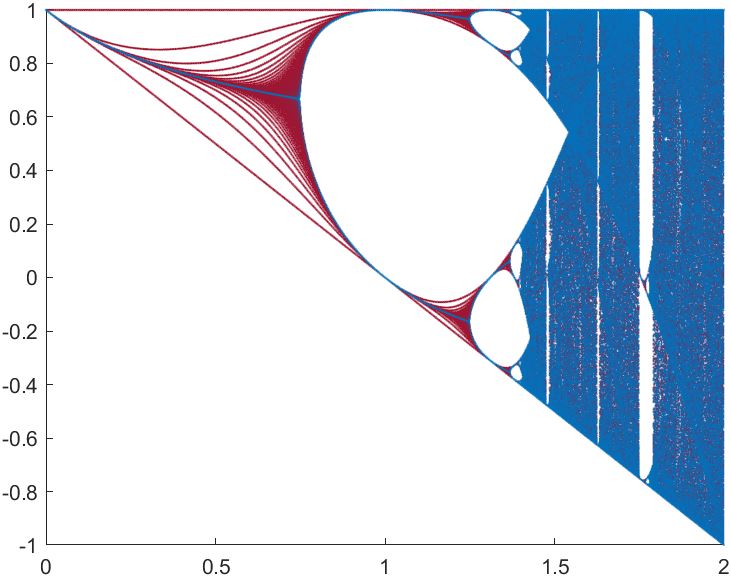
横坐标代表参数的数值，纵坐标表示该参数数值下序列可能的取值，n>100再开始画图是为了让序列通过迭代稳定下来，事实上我么可以不设置n>100，同时将颜色设置为随着n变化的渐变色，可以发现几乎看不出渐变来，该序列稳定的很快(以下是绘图部分代码的微调)：

c1=[0 0.4470 0.7410];
c2=[0.6350 0.0780 0.1840];
N=1000;
for n=1:N
    x=f(x,r);
    plot(r,x,'.','Color',(n.*c1+(N-n).*c2)./N,'MarkerSize',2);
    drawnow
end

当然我们可以设置n为奇数和偶数时绘制不同颜色，下图所示，对于该系统而言，其序列的数值是反复横跳的(以下是绘图部分代码的微调)：

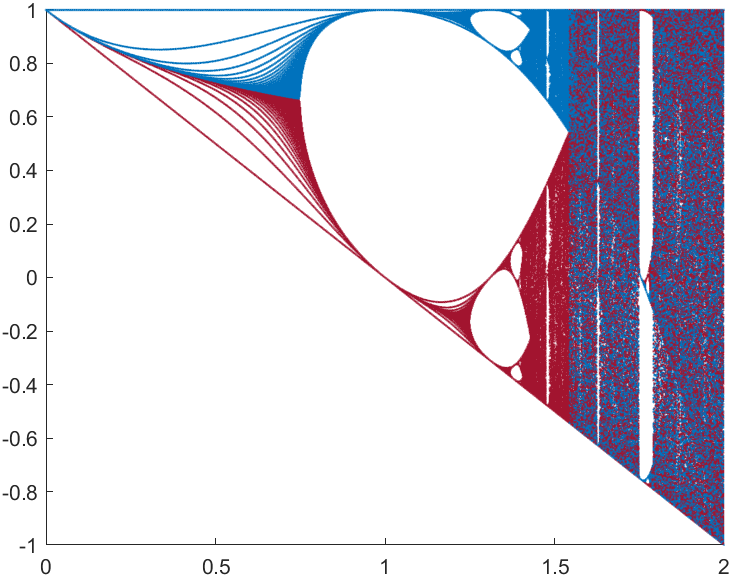
当然可以设置更多颜色：

for n=1:1000
    x=f(x,r);
    switch mod(n,4)
        case 3,plot(r,x,'.','Color',[0.4660 0.6740 0.1880],'MarkerSize',2);
        case 2,plot(r,x,'.','Color',[0.8500 0.3250 0.0980],'MarkerSize',2);
        case 1,plot(r,x,'.','Color',[0 0.4470 0.7410],'MarkerSize',2);
        case 0,plot(r,x,'.','Color',[0.6350 0.0780 0.1840],'MarkerSize',2);
    end
    drawnow
end

2.二维离散分岔图

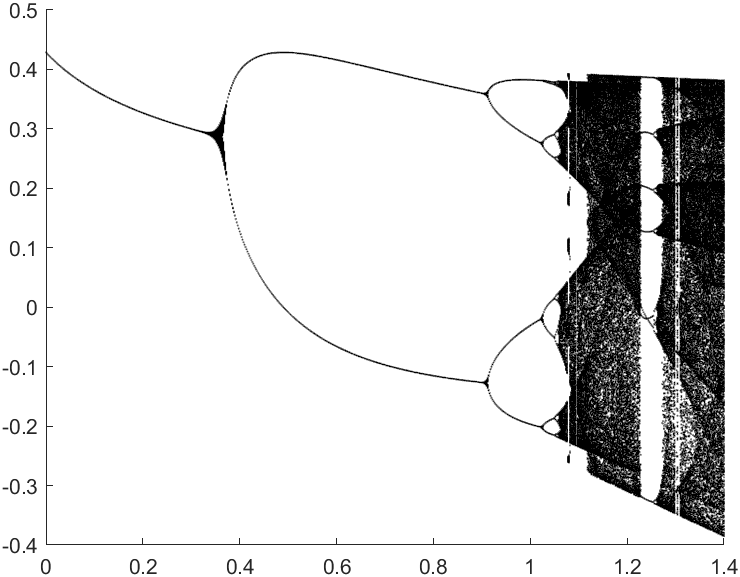
绘制Henon系统的分岔图：

定住b值不变，改变a值，观察y序列，不同b值时绘制效果不同：

% x(n+1)=1+y(n)-a*x(n)^2
% y(n+1)=b*x(n)
% Henon系统
hold on

fx=@(x,y,a)1+y-a.*x.^2;
fy=@(x,b)b.*x;
a=0:.002:1.4;b=0.2;
x=0;y=0;

for n=1:800
    lx=x;
    ly=y;
    x=fx(lx,ly,a);
    y=fy(lx,b);
    if n>100 % 稳定后开始绘图
        plot(a,y,'k.','MarkerSize',1);
        drawnow
    end
end

b=0.2时绘制效果

b=0.3时绘制效果

3.封面图绘制

经典体现理科生工科生艺术情怀环节，我们怎么能够将分岔图的美忽视？

感觉大家很多也是因为看封面图点进来的，虽然不短，但还是把代码放一下叭，原理很简单，构造一个矩阵统计各个位置点数量，然后依据点数量映射到颜色：

图一

% x(n+1)=1+y(n)-a*x(n)^2
% y(n+1)=b*x(n)
% Henon系统

fx=@(x,y,a)1+y-a.*x.^2;
fy=@(x,b)b.*x;
a=0:.002:1.4;b=0.3;
x=0;y=0;

% 填充矩阵
pntMat=zeros(451,701);
for n=1:12000
    lx=x;
    ly=y;
    x=fx(lx,ly,a);
    y=fy(lx,b);
    disp(['进度:[',num2str(n),'/12000]']);
    ty=round((y+0.4)*500);
    ta=a*500;
    index=round((ta).*451+ty);
    pntMat(index)=pntMat(index)+1;
end

% 矩阵上下翻转(坐标y轴方向与图片序数相反)
pntMat=flipud(pntMat);
% 绘图
imagesc(pntMat);
caxis([0,50])
ax=gca;
hold on;
ax.XTick=[];
ax.YTick=[];

% 颜色映射
map=[0.1294 0.0549 0.1725;0.2196 0.1608 0.2902;0.3882 0.1804 0.4941;
     0.4392 0.1922 0.4706;0.5333 0.2235 0.4392;0.6471 0.2588 0.3686;
     0.7137 0.2745 0.3294;0.7725 0.3059 0.2902;0.8510 0.3725 0.2275;
     0.9137 0.4196 0.1804;0.9608 0.5020 0.2000;0.9765 0.5529 0.2078;
     0.9804 0.6431 0.2549;0.9843 0.6627 0.2706;0.9765 0.7176 0.3412;
     0.9765 0.7686 0.4000;0.9765 0.8118 0.4902;0.9725 0.8510 0.5961;
     0.9882 0.9020 0.6667;1.0000 0.9451 0.8431;1.0000 0.9961 0.9804;
     1.0000 1.0000 1.0000];
Xi=1:size(map,1);Xq=linspace(1,size(map,1),800);
map=[interp1(Xi,map(:,1),Xq,'linear')',...
     interp1(Xi,map(:,2),Xq,'linear')',...
     interp1(Xi,map(:,3),Xq,'linear')'];
 colormap(map)

图二

% x(n+1)=1-r*x(n)^2
% (r∈(0,2),x∈[-1,1])的分支混沌图。
f=@(x,r)1-r.*x.^2;
r=0:.0025:2;
x=0; % x初值

pntMat=zeros(801,801);

for n=1:20000
    x=f(x,r);
    disp(['进度:[',num2str(n),'/20000]']);
    if n>1 % 稳定后开始绘图
        tx=round((x+1)*400);
        tr=r*400;
        index=round((tr).*801+tx);
        pntMat(index)=pntMat(index)+1;
    end
end

% 为了减少锯齿化高斯模糊一下
pntMat=imgaussfilt(pntMat,0.3);

% 矩阵上下翻转(坐标y轴方向与图片序数相反)
pntMat=flipud(pntMat);
% 绘图
imagesc(pntMat);
caxis([0,80])
ax=gca;
hold on;
ax.XTick=[];
ax.YTick=[];

% 颜色映射
map=[0.1400    0.1100    0.1500
    0.2800    0.0900    0.4100
    0.2700    0.2100    0.5100
    0.2300    0.3200    0.5500
    0.1900    0.4200    0.5600
    0.1500    0.5100    0.5600
    0.1200    0.5800    0.5500
    0.1400    0.6700    0.5100
    0.2400    0.7300    0.4600
    0.3900    0.8000    0.3700
    0.5900    0.8500    0.2500];
Xi=1:size(map,1);Xq=linspace(1,size(map,1),800);
map=[interp1(Xi,map(:,1),Xq,'linear')',...
     interp1(Xi,map(:,2),Xq,'linear')',...
     interp1(Xi,map(:,3),Xq,'linear')'];
 colormap(map)

到此这篇关于基于Matlab实现离散分岔图的绘制的文章就介绍到这了,更多相关Matlab离散分岔图内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！