汇编语言基础理解计算机底层技术原理

目录

• 前言
• 1.机器语言
• 2.进制思想本质
• 3.二进制
• 我们为什么学习理解二进制？
• 4.数据宽度
• 5.有符号数和无符号数
• 6.原码反码补码
• 7.位运算
• 8.位运算的加减乘除
• 9.汇编语言环境说明
• 10.寄存器的理解
• 11.内存
• 12.总结

前言

备注：该技术博客的内容是我根据技术视频整理与总结的（并非复制粘贴）。原视频源于【遇见狂神说】

如果我们想要做高级程序员，汇编语言是我们必经之路，汇编让我们跳出传统的编程思想，往底层学习，对我的技术提升非常非常重要。总而言之，想要成为高级程序员，我们必须要学会汇编语言，汇编语言是非常重要的计算机底层技术，一般用于底层的编写。不懂汇编的程序员算不上一个好的程序员，充其量是一个熟练使用某种语言的工程师，而编程高手一定要研究底层。

1.机器语言

何为语言，就是人和人之间交流的工具。而汇编语言就是计算机的语言。

机器语言（二进制）：

主流的电子计算机使用二进制，计算机只认识 0和1，因为在电路中只有两种状态，要么通电要么断电，我们用数字表示这两种状态就是0和1，我们可以用0和1与计算机交流。

机器语言就是由0和1构成的语言，我们很难理解，几乎看不懂。而我们需要将这些复杂的机器语言（一堆0和1的数字）简化，就需要助计符（INC DEC MUL DIV等）,也就是汇编语言。

我们掌握了汇编语言就可以操作计算机的底层，深入一点就是可以直接操作计算机里面的 位。
汇编语言助记机器语言，所以说我们学会了汇编语言就学会了机器语言。

学习汇编就是为了理解计算机怎么操作，每一行代码怎么被计算机执行，这些原理非常重要！

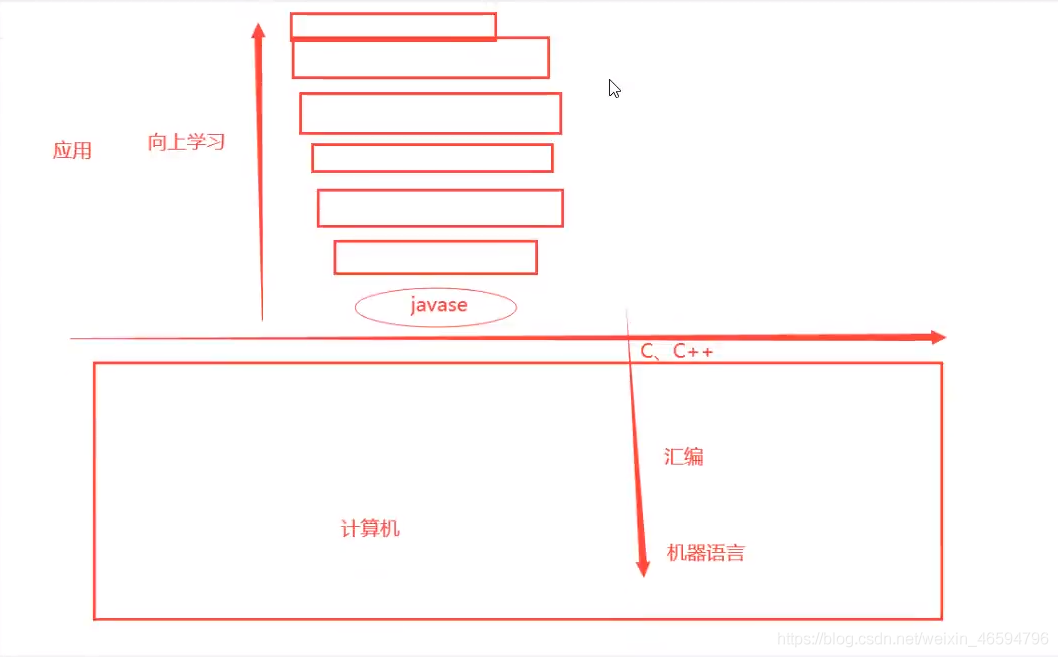
2.进制思想本质

学习进制的障碍：
很多人搞不懂进制的主要原因是因为我们从小接受了十进制的概念，逢十进一的原则深入人心。
人本能的选择就是 十进制。

常见进制：
1进制：逢一进一，1 1
2进制：逢二进一，计算机进制
8进制：逢八进一，8个符号组成：0 1 2 3 4 5 6 7
10进制：逢十进一，10个符号组成：0 1 2 3 4 5 6 7 8 9
16进制： 逢十六进一，16个符号组成：0 1 2 3 4 5 6 7 8 9 a b c d e f

进制其实非常简单，只需要会 查数。

测试：

进制可以自定义：
小朱同学的十进制：0 2 4 7 8 a b r d f，可以随便定义。
由此我可以使用进制加密，防止被爆破（暴力破解）。

3.二进制

目前的计算机（电子计算机）使用二进制 0 1

现在的计算机（电子计算机）：
都是通过集成电路来实现电路的有电和无电，高电平和低电平，表现出来两个值0 1。

由于二进制写起来非常麻烦，我们就需要简写二进制，所以我们就去写16进制。

拓展：
未来的量子计算机：（传道）
可以实现量子计算的机器。

量子计算机的 单位：昆比特。也就是所谓的（量子比特），量子的两态（光子，磁场）来表示。
量子的计算速度远远超越了现在的电子计算速度。
光子：正交偏振方向。
磁场：电子的自旋方向。

如今我们已经到了21世纪，计算力已经快到尽头了，没办法突破（落伍）的本质问题！
我们想要突破这个本质问题，就要使用量子计算机。核心要素就是提高计算机的计算力！

2019年，Google研究人员展示其最新54比特量子计算机，该计算机只用200秒便可计算完毕当前世界最大的超级计算机需1万年进行的运算。
2020年.6.18，霍尼韦尔公司推出了量子体积64的量子计算机！
霍尼韦尔还表示，将在一年之内得到至少10个有效量子比特，相当于1024个量子体积。
如果可以量产，大规模普及到民用之后，我们这些程序员是第一批使用他们的人。因为我们要
针对量子计算机写程序。

我们为什么学习理解二进制？

如果我们了解寄存器，内存，位的概念，计算机底层的每一个位都是有含义的（汇编入门理解的基础）。每一个0和1都代表一种状态，计算机会按照这种状态去执行特定的功能。程序运行时候会快速发生变化，每一个变化就会产生不同的状态，就比如：移动鼠标为什么会动，这底层如何实现非常的复杂。

4.数据宽度

计算机的内存是有限制的，内存不可能是无穷大的。所以我们就需要给数据增加数据宽度。

在计算计领域，我们要记住：所有的内存，所有的操作，都要给数据加上宽度，尤其是C,C++,Java这种强类型语言，都需要定义数据类型！为什么要需要定义类型？因为计算机底层需要我们这些数据定义宽度。

有了宽度，就有了一些基本的量。常用量包含字节，字，双字等…

位 (bit)：0 1
字节 (byte)：（8位） 0-0xFF
字 (word)：0-0xFFFF
双字 (dword)：0-0xFFFFFFF

在计算机中，每一个数据都需要给它定义类型。定义类型的原因就是给它定义宽度。在内存中的宽度。

5.有符号数和无符号数

计算机它并不知道我们写的数字是正还是负。我们可以通过正负号来判断，而计算机如何去表示正负呢？我们接下来了解一下！

数据都是有宽度的。 那么每个数据代表什么意思呢？

规则
就好比我们解析一个音频：比如说为什么网易云可以放出MP3？那是因为有个MP3的编码格式，我们根据这个格式解码才能放出声音对应的格式。如果是一个视频就要遵守视频的解码规则…

现在我们需要给二进制解码增加一个规则。
1.无符号数规则：
你这个数字是什么，那就是什么，无关正负。

1 0 0 1 1 0 1 0  转换十六进制为： 0x9A   十进制为：154

2.有符号数规则：
最高位是符号位。 如果最高位是1，就代表一个负数。如果最高位是0，就代表是一个正数。

1 0 0 1 1 0 1 0  如何转换十六进制？

这里就涉及一套计算机规则：就是原码反码补码。

6.原码反码补码

为什么学原码反码补码？
因为我们之后要用它来计算。

编码规则：（无符号数编码规则没什么可说的，写的数字是什么就是什么）

有符号数编码规则有三种状态：**原码，反码，补码。**我们来依此学习一下这三种状态。

1.原码： 最高位是符号位，对齐它的位进行本身的绝对值即可。
2.反码： 分为正数和负数

正数：反码和原码相同。负数：符号位一定是1，其余位对原码取反。

3.补码：

正数：补码和原码相同负数：符号一定是1，对反码进行+1

举个例子：

现在我说的这些都是 8 位 

如果是正数，都是一样的。
对1取值：
原码：0 0 0 0  0 0 0 1
反码：0 0 0 0  0 0 0 1
补码：0 0 0 0  0 0 0 1

如果是负数
对-1取值：
原码：1 0 0 0  0 0 0 1
反码：1 1 1 1  1 1 1 0
补码：1 1 1 1  1 1 1 1

对-7取值：
原码：1 0 0 0  0 1 1 1
反码：1 1 1 1  1 0 0 0
补码：1 1 1 1  1 0 0 1

对3+5取值：
3的二进制是 11
5的二进制是 101
加起来是 1000

我们现在要理解一句话，如果看到一个二进制的数字。需要了解它是有符号数还是无符号数。

拓展：
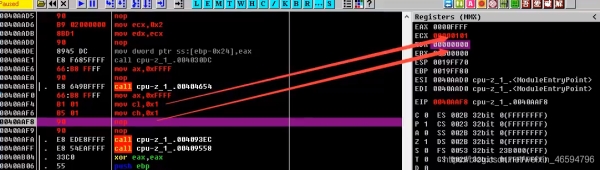
接下来先给大家扩展一个寄存器：里面可以存值。通用的寄存器有8个，可以存储任意的值。我可以通过mov指令向某个寄存器存值，如下图：

现在我要写一个-1，我们来看看会有怎样的区别：

这里的FFFF FFFF是我们存的-1在寄存器中的值。一个F就是 1111，首先最高位的值是1，所以代表他是一个负数。我们正常存1的时候首位明显是0，而存-1就变成FFFF FFFF。因为-1在计算机中是补码的方式存储的，所以负数在我们计算机中使用补码方式存储的。所以学习通过直接操作查看是最有效的。

FFFF FFFF代表三十二个1，如果是无符号的话，代表它是正数。如果是有符号的话，代表它是一个负数，是有很大的本质区别的。

我们搞懂原码反码补码之后，以后知道了计算机底层是怎么存储数字的：正数就正常的存，因为无论原码反码补码，正数都是相同的。而负数主要存的是补码！如果了解了这些，就是为了接下来的位运算打交道。

7.位运算

我们之前说过，计算机现在可以存储所有的数字（正数，浮点数，字符），不论正数还是负数都可以存储。如果可以把这些数字加以运算，我们就可以做到世界上的一切。无论多复杂的运算，底层都是加减乘除。我们只要把位运算的位如何操作运算记住、突破就可以了。

接下来我们学习位运算。

首先有一个面试高频题：2*8最高效的计算方式？
这道题不论怎样都非常慢，只有通过位运算才是最快的，比如左移、右移。而且要记住一句话：很多底层的调试器（例如C语言调试器），当我们手写调试器的时候就需要通过位来判断CPU的状态。

位运算就是我们常说的与或非 异或运算等…我们一个一个来看：

与运算：

在JAVA语言中用 & 符号去表示，但是在汇编中用 and 代表与。下面图片方便我们的理解：

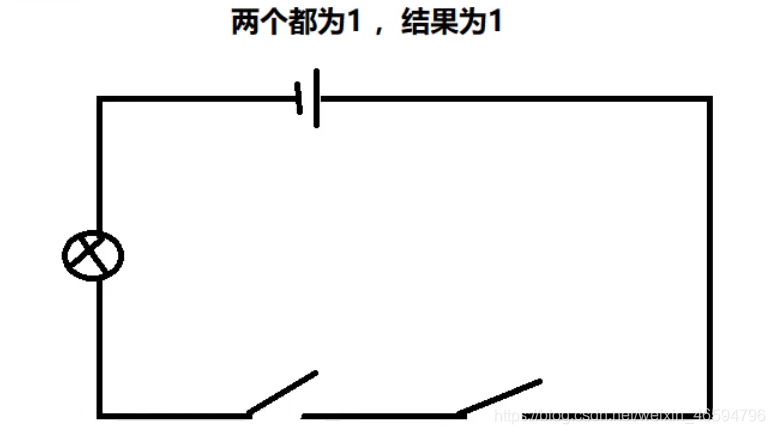
1011 0001
1101 1000
-------------------- 与运算的结果
1001 0000

或运算：
在JAVA语言中用（|）表示，在汇编语言中用or表示，同样根据或运算也有一张电路图可以帮助理解：

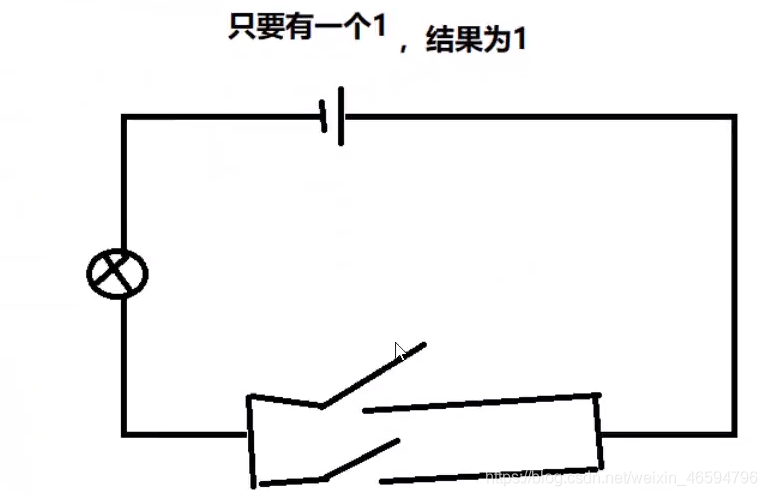
1011 0001
1101 1000
--------------- 或运算
1111 1001

异或运算：
在我们JAVA语言中用（^）表示，在汇编语言中xor表示。说白了记住一句话：不一样就是1。再来一张电路图理解：

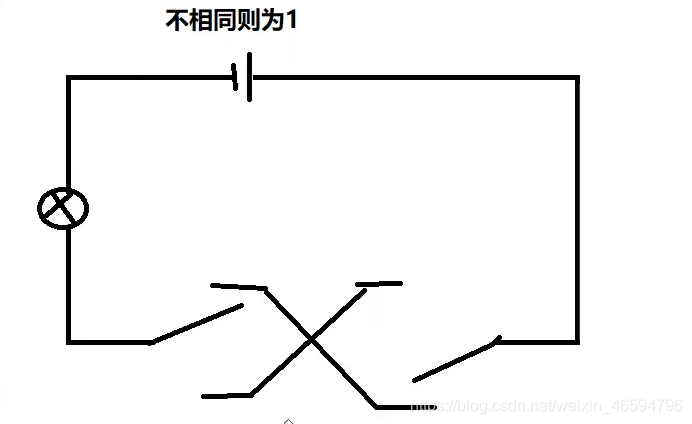
1011 0001
1101 1000
--------------------异或运算
0110 1001

非运算（单目运算符）：
我们所谓的取反（非），在JAVA语言中是（！）,在C语言中是（~），在汇编语言中是not。
说白了一句话：0就是1，1就是0。

1101 1000
----------------- 非运算
0010 0111

通过这些可以完成我们的加减乘除。怎么通过位运算实现加减乘除呢？

位运算：
它是一个移动位，分为左移，右移。（左移*2，右移/2）。

左移（shl <<）:

0000 0001  所有的二进制位全部左移若干位，高位就丢弃，低位补0
0000 0010

右移（shr >>）:

0000 0001  所有二进制全部右移若干位，低位就丢弃，高位补0或1（根据符号位决定，负数补1，正数补0）
0000 0000

如果想要取值(C++)
int a = 10;
printf("%d\n",a>>2);

总结： 汇编的本质就是操作二进制。

通过二进制、位运算实现 加减乘除。

8.位运算的加减乘除

接下来我们讲，如何通过位运算实现加减乘除。我们的计算机只认识0和1，但是基本的数学是建立在加减乘除上。（加法搞定，一切都搞定了）

举个例子：求4+5？

计算机是如何操作的呢？
0000 0100
0000 0101
-------------------------（加法，计算机是不会直接加）
0000 1001

那么计算机的实现原理是什么呢？
怎么将两个数加起来？核心是：异或。

第一步，异或（不一样为1）：如果不考虑进位，异或就可以直接出结果
0000 0100
0000 0101
-------------------------
0000 0001
第二步，计算机在这个异或的结果上在做与运算操作：
与运算（判断进位），如果与运算结果为0，那么就没有进位。
0000 0100
0000 0101
-------------------------
0000 0100
第三步，将与运算的结果左移一位。
0000 0100 ——> 0000 1000 (进位的结果)
第四步，还是一个异或运算。（第一步异或出来的结果和第三步与运算的进位结果再一次异或）
0000 0001
0000 1000
------------------------
0000 1001
第五步，再去做一个与运算，判断它是否有进位。（与第二步一样）
0000 0001
0000 1000
------------------------
0000 0000
最后一步与运算结果为
0000 0000
电路都断了，灯泡全灭，通过不了，所以最终结果就是：
与运算为0的结果的上一个异或运算结果：
0000 1001 （二进制的9）
如果与运算不为0，继续循环。

举个例子：求4-5？

我们说了，计算机没有所谓的减法，那么计算机是如何操作的呢？
4-5 说白了就是 4+(-5)
0000 0100
1111 1011 (代表二进制的-5)
------------------------（减法，计算机是不会直接减）
1111 1111（8个1就是ff,所以ff在十进制中代表-1）

0000 0100
1111 1011
------------------------ 异或(如果不考虑进位，异或就可以直接出结果)
1111 1111

0000 0100
1111 1011
------------------------ 与运算（判断进位），如果与运算结果为0，那么就没有进位。
0000 0000

最终结果
1111 1111 (十六进制的ff，十进制的-1)

举个例子：
乘法： x * y，本质就是y个x相加，还是加法。
除法： x / y，本质就是减法，就是x能减去多少个y。

结论：
计算机只会做加法！

9.汇编语言环境说明

目前为止，我们可以从零设计一套自己的进制规则。自己设计电路来实现加减乘除。但是最终乘除的结果是一个二进制，例如：我们有32个灯泡，就可以显示32个数值，最终亮起灯泡的数就是最终的结果。手动转换这个结果和值！（十进制和二进制的转换）

机器语言并不会做很多事情，它很“笨”。机器语言说白了就是位运算，（加减乘除）
都是电路来实现的。这就是计算机最底层的本质。

但是，我们发现，学完了这些东西依旧是不懂，只是对现在的程序做了一些提高的理解。但是想通过理解写程序写不出来，难道我们真的写不出来吗？

通过机器语言来实现加法计算器，这就是设计电路。

我们通过指令来代替我们的一些二进制编码！比如说：刚才的加法运算是通过各种操作能否通过一个符号计算呢？比如说我就想叫它（ADD指令），假设我给计算机发一个ADD指令，它通过识别我的指令转换成机器语言（也就是编译）ADD指令转换为二进制操作。

汇编语言说白了，底层还是二进制，但是二进制写起来太麻烦了。这个时候我们通过汇编指令给计算机发一些操作，然后让计算机执行。这个地方就要涉及到编译器！因为我们说的编译命令不是机器直接能识别的，需要把命令转码，转成计算机认识的信息，不然没法识别。这个时候就涉及到编译器的发展。

如果学底层，一定不要用特别智能的编译器（IDEA，VSCODE等），就是用越远古的越好（记事本，vim等）。很多人学习C语言使用，用的是vim编辑器去写C语言，用gcc来执行。这是学习C的正确方式。底层的大佬几乎都是最原始的idea。

在学习汇编之前，先要掌握环境的配置：

Vc6（程序到汇编的理解，通过C语言实现）

OD

抓包工具

加密解密工具

尽量不要使用java去学汇编，学完了汇编去学jvm就会觉得很简单。但是如果我学java再学汇编就有点痛苦，建议使用C++学汇编。因为C++可以直接看到内存的地址，可以打印通过指针直接找到内存的地址，通过地址判断信息。

学汇编不是为了写代码，就是为了理解程序的本质。
如果懂汇编，就能够理解所有复杂的概念。

如果我们是一个做应用的程序员，别人调试不了的程序，如果学过汇编，都可以调试。因为知道底层堆栈到底做了什么。如果是做安全的（反外挂，反病毒），就要理解汇编到二进制的全部知识。

现在的计算机至少是32位，还有的是64位。我们要知道，它是由32位演化过来的。底层架构没有发生变化，只是多了寄存器，主要是寻址能力增加。

汇编入门： 了解汇编和程序的对应关系，程序的本质即可。

学会了这些，不理解的java原码就理解了。汇编非常重要！这对我们向上学习有很大的帮助。有些编程技术学进不去，很大原因就是因为底层不够。底层精通了在学习编程语言就发现太轻松了！

10.寄存器的理解

学习汇编，要学习三个重要的概念：

寄存器

内存

汇编指令

通用寄存器：可以存储任何值

存储数据：CPU>内存>硬盘
CPU分为32位和64位。

32位：8 16 3264位：8 16 32 64

32位的通用寄存器只有8个：

寄存器中的存值范围：0 ~ FFFFFFFF

计算机如何向寄存器中存值呢？
对于二进制来说，就是直接修改值。但是修改值需要找到对应的位置，所以才有内存地址。

mov指令

mov  存的地址，存的数
mov  存的地址1，存的地址1

可以将数字写入到寄存器，可以将寄存器中的值，写到寄存器。

计算机的本质：计算力！ 就是为了计算！（鼠标光标在移动都是在计算）

不同的寄存器：

32位代表八个F（FFFF FFFF），一个F代表4位（1111）
		FFFF	FF
32位    16位    8位
EAX     AX		AL
ECX		CX		CL
EDX		DX		DL
EBX		BX		BL
ESP		SP		AH
EBP		BP		CH
ESI		SI		DH
EDI		DI		BH

对于8位：L代表低8位，H代表高8位
16位是FFFF 高八位占前两个FF，低八位占后两个FF

除了这些通用寄存器之外，那么其他的寄存器每一位都有自己特定的功能（比如：开机关机）。
我们一般写值都会写到通用寄存器中。

11.内存

寄存器很小，而且不够用。所以我们会把数据放到内存中。

有句话：每个应用程序进程都有4GB的内存空间。 程序用的内存就是空头支票，虽然每个应用程序的进程都有4GB内存空间，但是真正到机器上使用时候并没有那么大。

程序真正运行的时候，才会用到物理内存。

1B = 8bit
1KB = 1024B
1MB = 1024KB
1GB = 1024MB

假设是4GB内存电脑，就等于4096m => 最终计算为位，就是可以存储的最大容量。
计算机中的内存地址很多，空间很大。

内存地址：
存一个数：占用大小，数据宽度。存到哪里呢？

计算机中的内存地址很多，空间很大。我们要给空间取名字，每个空间分配一个地址，名字。

这些给内存起的编号就是我们的内存地址。32位（8个十六进制的值）

32位：决定寻址能力！
FFFFFFFF + 1 = 100000000,最大的值。
位是怎么限制内存大小呢？
100000000 内存地址 * 8位 ：800000000。
转换为十进制 / 8：4,294,967,296字节。
按照规则/1024最终发现就是 4GB（不能超过）。
64位,绰绰有余。

所以每个内存地址都有一个编号：可以通过编号向里面存值

很多人学C语言搞不懂指针，原因就是 不懂内存。

内存如何存值？（mov指令）
存值需要知道数据宽度（byte word dword）,地址位置(自定义：0xFFFFFFFF)
不是任意的地址都可以写东西，只有程序申请过的内存地址我们才可以使用。

汇编如何向内存中写值：
mov  数据宽度  内存地址，1

mov  byte ptr ds:[0x19ff70],1

传递的值的大小一定要和数据宽度要相等，如果大放不进去。

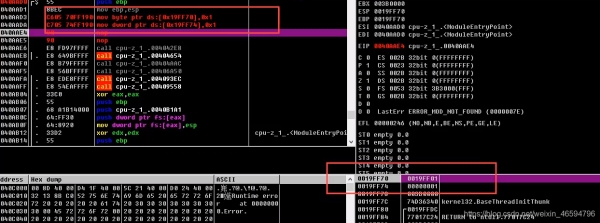
内存地址有多种写法：

ds:[0x19FF70+4]（内存地址偏移）：加 偏移（4），地址就变成了：0x19FF74ds:[eax]（寄存器）：把寄存器中的值放到内存中。ds:[eax + 4]（寄存器偏移）

以数组为例：
ds:[reg + reg * {1,2,4,8}]
ds:[reg + reg * {1,2,4,8} + 4] 偏移

12.总结

学到这里，在学其他的汇编内容已经很轻松了，包括学计算机操作原理也很轻松。
如果能够全部理解，再看自己写的程序就会豁然开朗很多。

以上就是汇编语言基础理解计算机底层原理的详细内容，更多关于计算机底层汇编语言的资料请关注我们其它相关文章！