C#数据结构之最小堆的实现方法

最小堆

基本思想：堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最小（大）堆，依次类推，最终得到排序的序列。

堆排序分为大顶堆和小顶堆排序。大顶堆：堆对应一棵完全二叉树，且所有非叶结点的值均不小于其子女的值，根结点（堆顶元素）的值是最大的。而小顶堆正好相反，小顶堆：堆对应一棵完全二叉树，且所有非叶结点的值均不大于其子女的值，根结点（堆顶元素）的值是最小的。

举个例子：

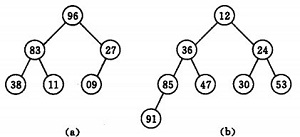
(a)大顶堆序列：（96, 83,27,38,11,09)

(b)小顶堆序列：（12，36，24，85，47，30，53，91）

实现堆排序需解决两个问题：

　　1. 如何将n 个待排序的数建成堆?

　　2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆?

首先讨论第二个问题：输出堆顶元素后，怎样对剩余n-1元素重新建成堆？

调整小顶堆的方法：

　　1）设有m 个元素的堆，输出堆顶元素后，剩下m-1 个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。

　　2）将根结点与左、右子树中较小元素的进行交换。

　　3）若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法 （2）.

　　4）若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法 （2）.

　　5）继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。

　　称这个自根结点到叶子结点的调整过程为筛选。如图：

再讨论第一个问题，如何将n 个待排序元素初始建堆？

　　建堆方法：对初始序列建堆的过程，就是一个反复进行筛选的过程。

　　1）n 个结点的完全二叉树，则最后一个结点是第n/2个结点的子树。

　　2）筛选从第n/2个结点为根的子树开始，该子树成为堆。

　　3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。

　　如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）

C#算法实现：

using System;
using System.Collections.Generic;

namespace StructScript
{
 /// <summary>
 /// 最小堆实现
 /// </summary>
 /// <typeparam name="T"></typeparam>
 public class BinaryHeap<T>
 {
  //默认容量为6
  private const int DEFAULT_CAPACITY = 6;
  private int mCount;
  private T[] mItems;
  private Comparer<T> mComparer;

  public BinaryHeap() : this(DEFAULT_CAPACITY) { }

  public BinaryHeap(int capacity)
  {
   if (capacity < 0)
   {
    throw new IndexOutOfRangeException();
   }
   mItems = new T[capacity];
   mComparer = Comparer<T>.Default;
  }

  /// <summary>
  /// 增加元素到堆，并从后往前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点
  /// </summary>
  /// <param name="value"></param>
  /// <returns></returns>
  public bool Enqueue(T value)
  {
   if (mCount == mItems.Length)
   {
    ResizeItemStore(mItems.Length * 2);
   }

   mItems[mCount++] = value;
   int position = BubbleUp(mCount - 1);

   return (position == 0);
  }

  /// <summary>
  /// 取出堆的最小值
  /// </summary>
  /// <returns></returns>
  public T Dequeue()
  {
   return Dequeue(true);
  }

  private T Dequeue(bool shrink)
  {
   if (mCount == 0)
   {
    throw new InvalidOperationException();
   }
   T result = mItems[0];
   if (mCount == 1)
   {
    mCount = 0;
    mItems[0] = default(T);
   }
   else
   {
    --mCount;
    //取序列最后的元素放在堆顶
    mItems[0] = mItems[mCount];
    mItems[mCount] = default(T);
    // 维护堆的结构
    BubbleDown();
   }
   if (shrink)
   {
    ShrinkStore();
   }
   return result;
  }

  private void ShrinkStore()
  {
   // 如果容量不足一半以上，默认容量会下降。
   if (mItems.Length > DEFAULT_CAPACITY && mCount < (mItems.Length >> 1))
   {
    int newSize = Math.Max(
     DEFAULT_CAPACITY, (((mCount / DEFAULT_CAPACITY) + 1) * DEFAULT_CAPACITY));

    ResizeItemStore(newSize);
   }
  }

  private void ResizeItemStore(int newSize)
  {
   if (mCount < newSize || DEFAULT_CAPACITY <= newSize)
   {
    return;
   }

   T[] temp = new T[newSize];
   Array.Copy(mItems, 0, temp, 0, mCount);
   mItems = temp;
  }

  public void Clear()
  {
   mCount = 0;
   mItems = new T[DEFAULT_CAPACITY];
  }

  /// <summary>
  /// 从前往后依次对各结点为根的子树进行筛选，使之成为堆，直到序列最后的节点
  /// </summary>
  private void BubbleDown()
  {
   int parent = 0;
   int leftChild = (parent * 2) + 1;
   while (leftChild < mCount)
   {
    // 找到子节点中较小的那个
    int rightChild = leftChild + 1;
    int bestChild = (rightChild < mCount && mComparer.Compare(mItems[rightChild], mItems[leftChild]) < 0) ?
     rightChild : leftChild;
    if (mComparer.Compare(mItems[bestChild], mItems[parent]) < 0)
    {
     // 如果子节点小于父节点, 交换子节点和父节点
     T temp = mItems[parent];
     mItems[parent] = mItems[bestChild];
     mItems[bestChild] = temp;
     parent = bestChild;
     leftChild = (parent * 2) + 1;
    }
    else
    {
     break;
    }
   }
  }

  /// <summary>
  /// 从后往前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点
  /// </summary>
  /// <param name="startIndex"></param>
  /// <returns></returns>
  private int BubbleUp(int startIndex)
  {
   while (startIndex > 0)
   {
    int parent = (startIndex - 1) / 2;
    //如果子节点小于父节点，交换子节点和父节点
    if (mComparer.Compare(mItems[startIndex], mItems[parent]) < 0)
    {
     T temp = mItems[startIndex];
     mItems[startIndex] = mItems[parent];
     mItems[parent] = temp;
    }
    else
    {
     break;
    }
    startIndex = parent;
   }
   return startIndex;
  }
 }
}

附上，测试用例：

using System;

namespace StructScript
{
 public class TestBinaryHeap
 {
  static void Main(string[] args)
        {
            BinaryHeap<int> heap = new BinaryHeap<int>();
            heap.Enqueue(8);
            heap.Enqueue(2);
            heap.Enqueue(3);
            heap.Enqueue(1);
            heap.Enqueue(5);

            Console.WriteLine(heap.Dequeue());
            Console.WriteLine(heap.Dequeue());

            Console.ReadLine();
        }
 }
}

测试用例，执行结果依次输出1，2。

总结

到此这篇关于C#数据结构之最小堆实现的文章就介绍到这了,更多相关C#数据结构最小堆实现内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！