详解R语言中的多项式回归、局部回归、核平滑和平滑样条回归模型

在标准线性模型中，我们假设 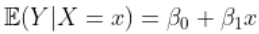。当线性假设无法满足时，可以考虑使用其他方法。

多项式回归

扩展可能是假设某些多项式函数，

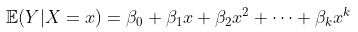
同样，在标准线性模型方法（使用GLM的条件正态分布）中，参数 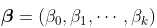 可以使用最小二乘法获得，其中  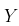在  。

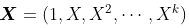即使此多项式模型不是真正的多项式模型，也可能仍然是一个很好的近似值 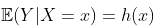。实际上，根据 Stone-Weierstrass定理，如果  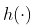在某个区间上是连续的，则有一个统一的近似值  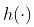，通过多项式函数。

仅作说明，请考虑以下数据集

db = data.frame(x=xr,y=yr)
plot(db)

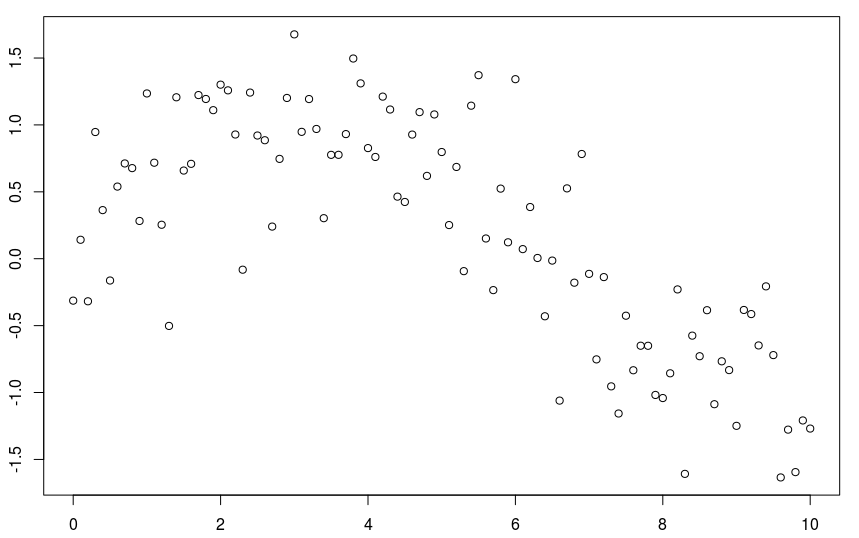
与标准回归线

reg = lm(y ~ x,data=db)
abline(reg,col="red")

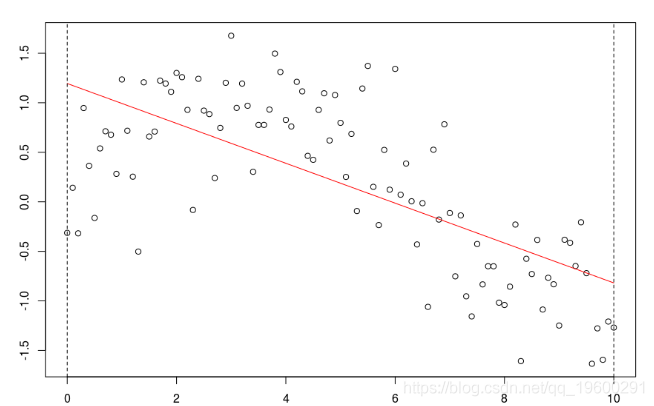
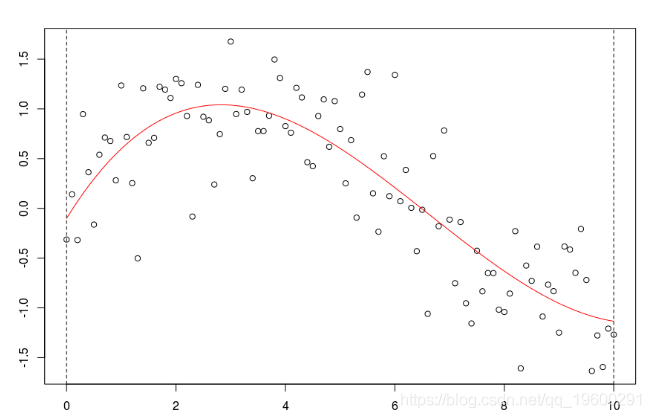
考虑一些多项式回归。如果多项式函数的次数足够大，则可以获得任何一种模型，

reg=lm(y~poly(x,5),data=db)

但是，如果次数太大，那么会获得太多的“波动”，

reg=lm(y~poly(x,25),data=db)

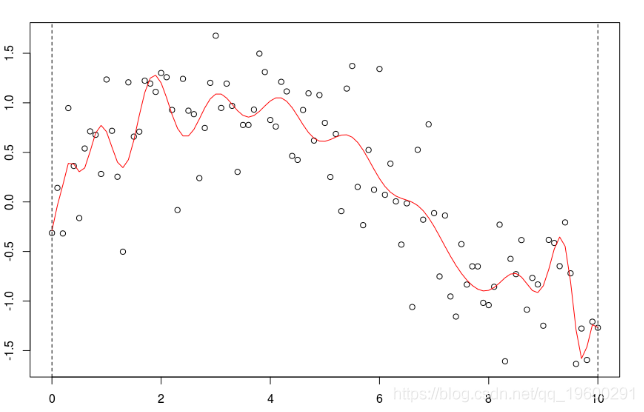
并且估计值可能不可靠：如果我们更改一个点，则可能会发生（局部）更改

yrm=yr;yrm[31]=yr[31]-2
lines(xr,predict(regm),col="red")

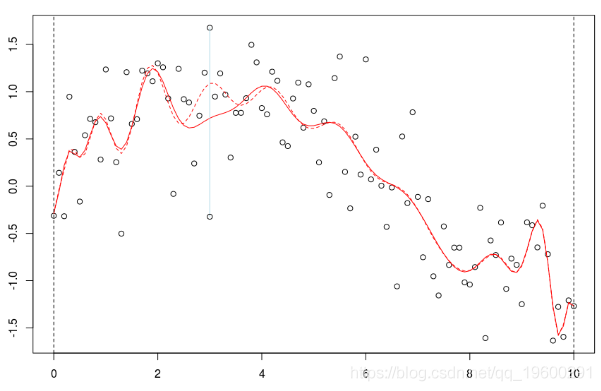
局部回归

实际上，如果我们的兴趣是局部有一个很好的近似值 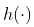 ，为什么不使用局部回归？

使用加权回归可以很容易地做到这一点，在最小二乘公式中，我们考虑

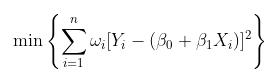
在这里，我考虑了线性模型，但是可以考虑任何多项式模型。在这种情况下，优化问题是

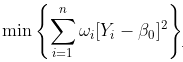可以解决，因为

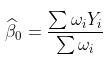
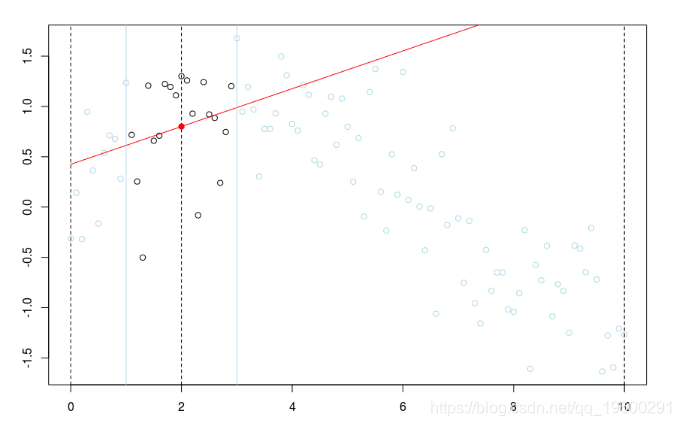
例如，如果我们想在某个时候进行预测 ， 考虑 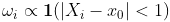。使用此模型，我们可以删除太远的观测值，

更一般的想法是考虑一些核函数 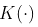 给出权重函数，以及给出邻域长度的一些带宽（通常表示为h），

这实际上就是所谓的 Nadaraya-Watson函数估计器 。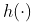
在前面的案例中，我们考虑了统一核 ，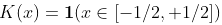

但是使用这种权重函数具有很强的不连续性不是最好的选择，尝试高斯核，

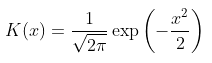
这可以使用

w=dnorm((xr-x0))
reg=lm(y~1,data=db,weights=w)

在我们的数据集上，我们可以绘制

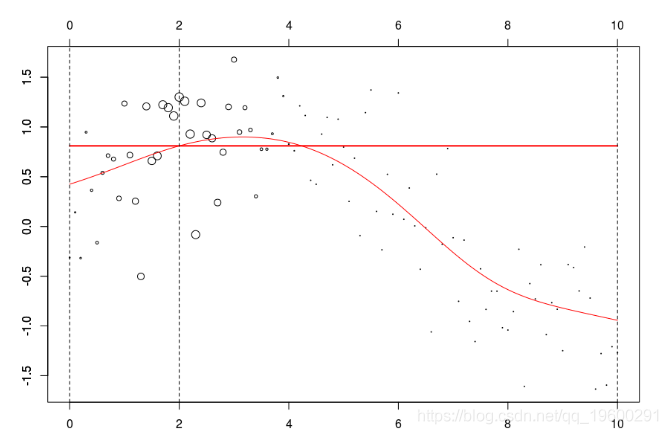
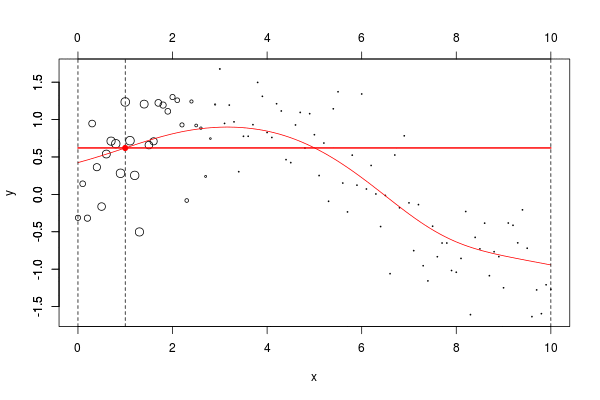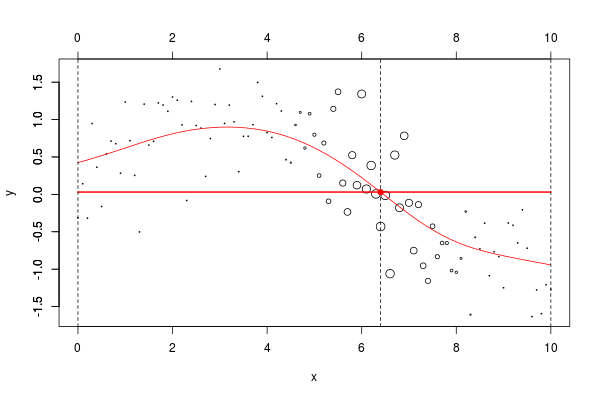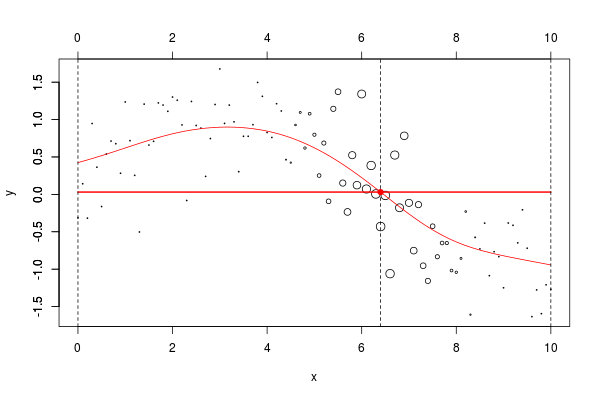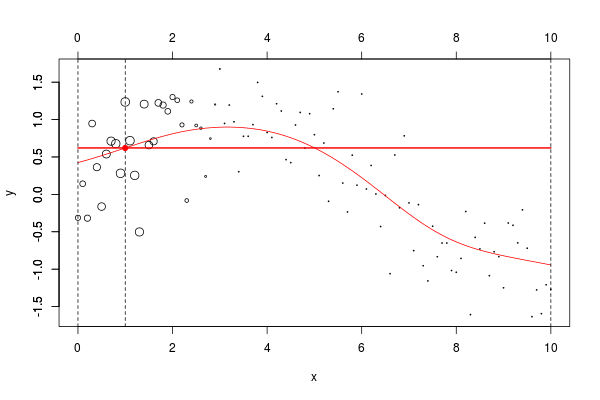
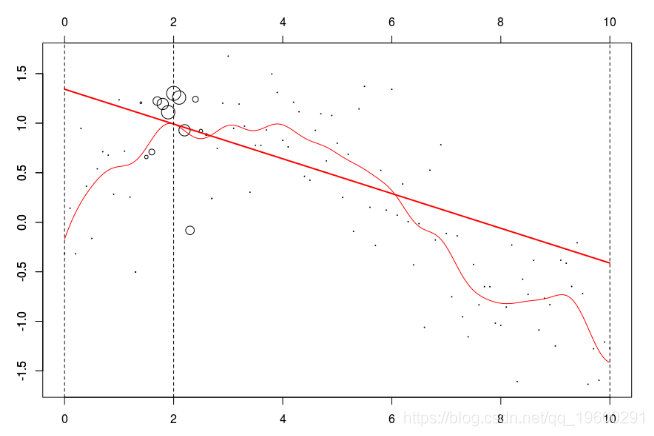
w=dnorm((xr-x0))
plot(db,cex=abs(w)*4)
lines(ul,vl0,col="red")
axis(3)
axis(2)
reg=lm(y~1,data=db,weights=w)
u=seq(0,10,by=.02)
v=predict(reg,newdata=data.frame(x=u))
lines(u,v,col="red",lwd=2)

在这里，我们需要在点2进行局部回归。下面的水平线是回归（点的大小与宽度成比例）。红色曲线是局部回归的演变

让我们使用动画来可视化曲线。

但是由于某些原因，我无法在Linux上轻松安装该软件包。我们可以使用循环来生成一些图形

name=paste("local-reg-",100+i,".png",sep="")
png(name,600,400)
for(i in 1:length(vx0)) graph (i)

然后，我使用

当然，可以考虑局部线性模型，

return(predict(reg,newdata=data.frame(x=x0)))}

甚至是二次（局部）回归，

lm(y~poly(x,degree=2), weights=w)

当然，我们可以更改带宽

请注意，实际上，我们必须选择权重函数（所谓的核）​​。但是，有（简单）方法来选择“最佳”带宽h。交叉验证的想法是考虑

 是使用局部回归获得的预测。

我们可以尝试一些真实的数据。

library(XML)

data = readHTMLTable(html)

整理数据集，

plot(data$no,data$mu,ylim=c(6,10))
segments(data$no,data$mu-1.96*data$se,

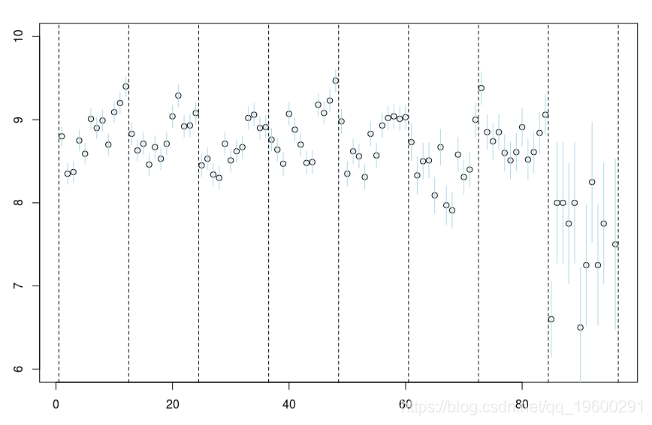
我们计算标准误差，反映不确定性。

for(s in 1:8){reg=lm(mu~no,data=db,
lines((s predict(reg)[1:12]

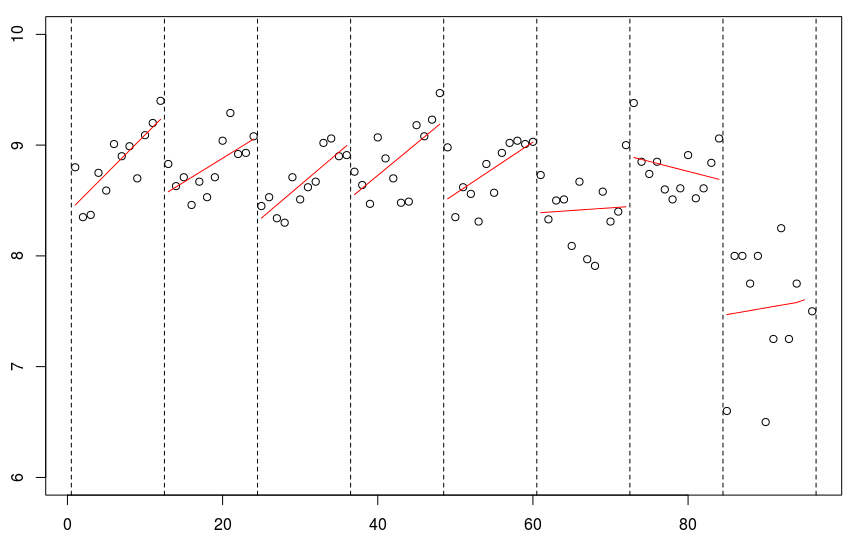
所有季节都应该被认为是完全独立的，这不是一个很好的假设。

smooth(db$no,db$mu,kernel = "normal",band=5)

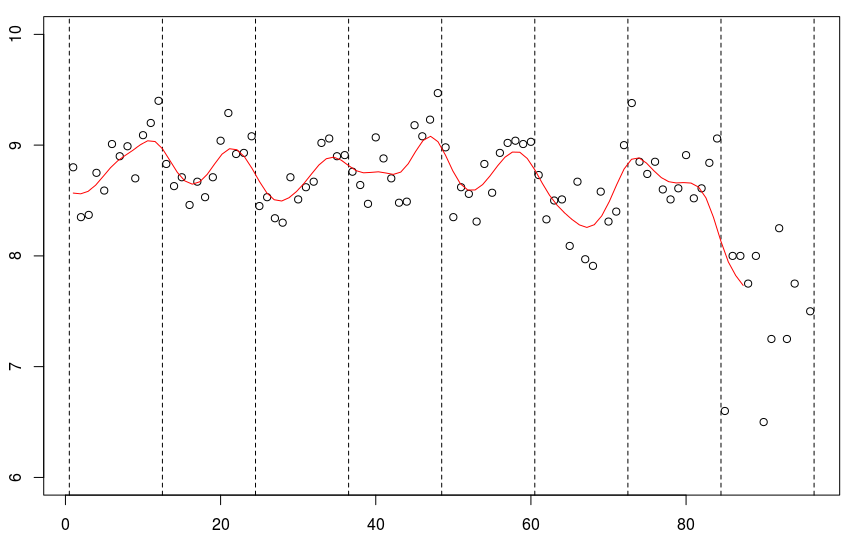
我们可以尝试查看带宽较大的曲线。

db$mu[95]=7

plot(data$no,data$mu

lines(NW,col="red")

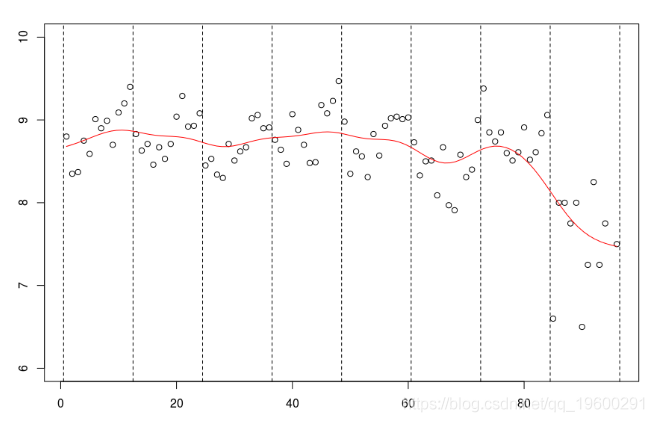
样条平滑

接下来，讨论回归中的平滑方法。假设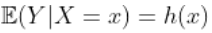 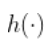，  是一些未知函数，但假定足够平滑。例如，假设  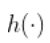是连续的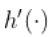，  存在，并且是连续的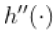，   存在并且也是连续的等等。如果  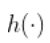足够平滑，  可以使用泰勒展开式。 因此，对于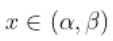 

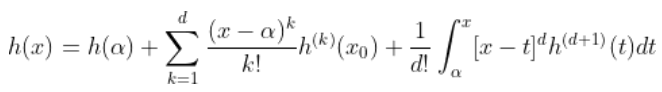
也可以写成

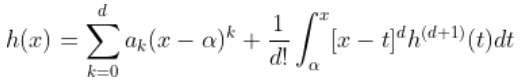
第一部分只是一个多项式。

使用 黎曼积分，观察到

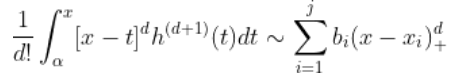
因此，

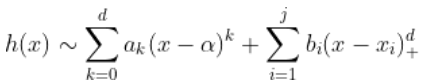
我们有线性回归模型。一个自然的想法是考虑回归 ，对于 

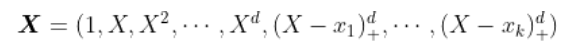
给一些节点 。

plot(db)

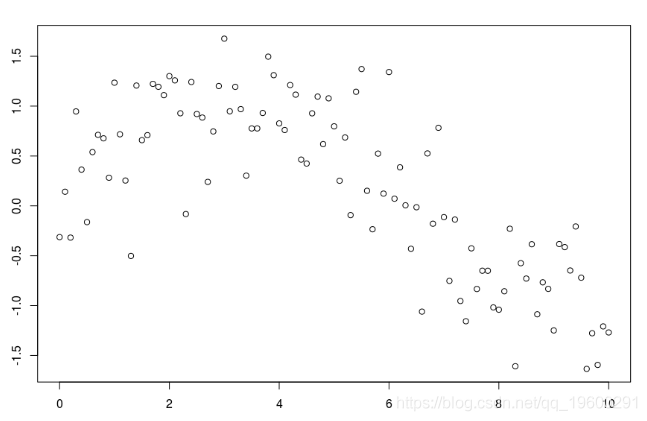
如果我们考虑一个节点，并扩展阶数1，

B=bs(xr,knots=c(3),Boundary.knots=c(0,10),degre=1)

lines(xr[xr<=3],predict(reg)[xr<=3],col="red")
lines(xr[xr>=3],predict(reg)[xr>=3],col="blue")

可以将用该样条获得的预测与子集（虚线）上的回归进行比较。

lines(xr[xr<=3],predict(reg)[xr<=3

lm(yr~xr,subset=xr>=3)

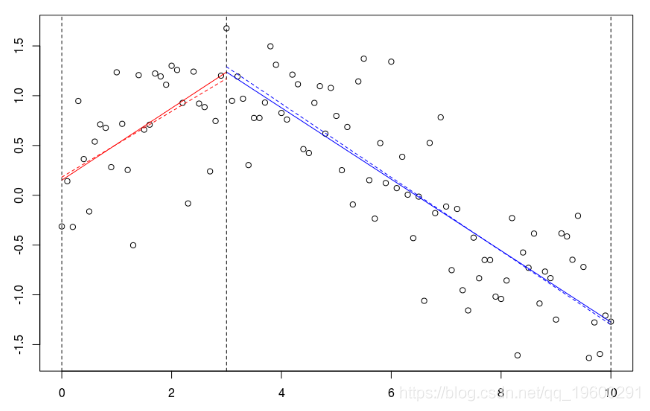
这是不同的，因为这里我们有三个参数（关于两个子集的回归）。当要求连续模型时，失去了一个自由度。观察到可以等效地写

lm(yr~bs(xr,knots=c(3),Boundary.knots=c(0,10)

回归中出现的函数如下

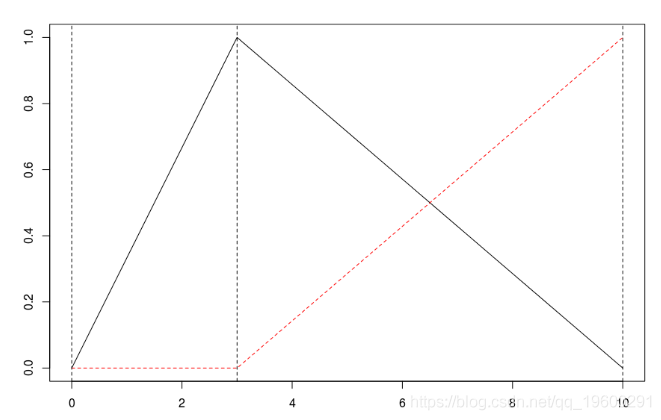
现在，如果我们对这两个分量进行回归，我们得到

matplot(xr,B

abline(v=c(0,2,5,10),lty=2)

如果加一个节点，我们得到

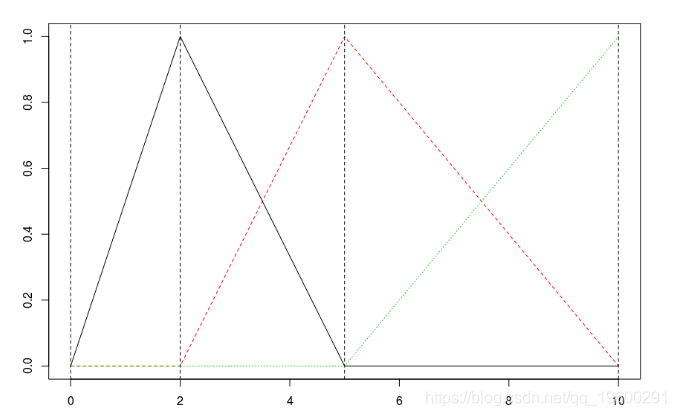
预测是

lines(xr,predict(reg),col="red")

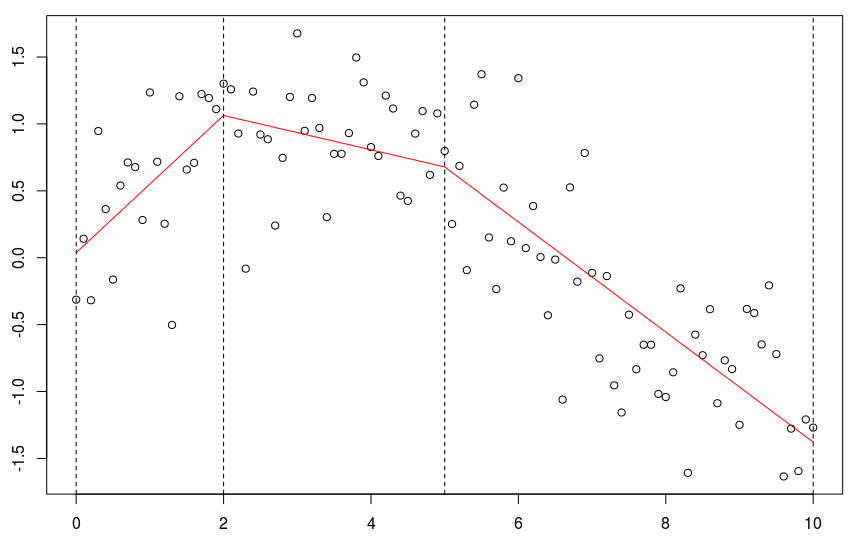
我们可以选择更多的节点

lines(xr,predict(reg),col="red")

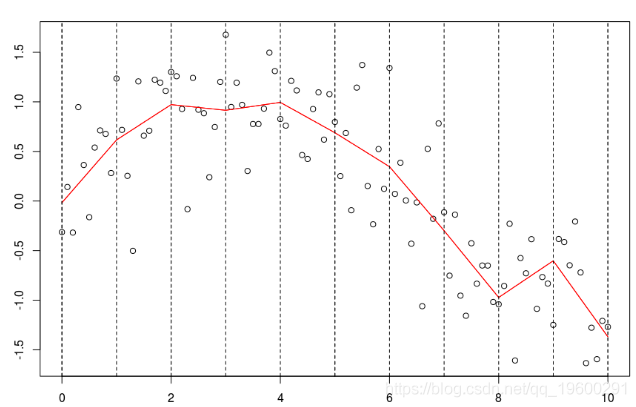
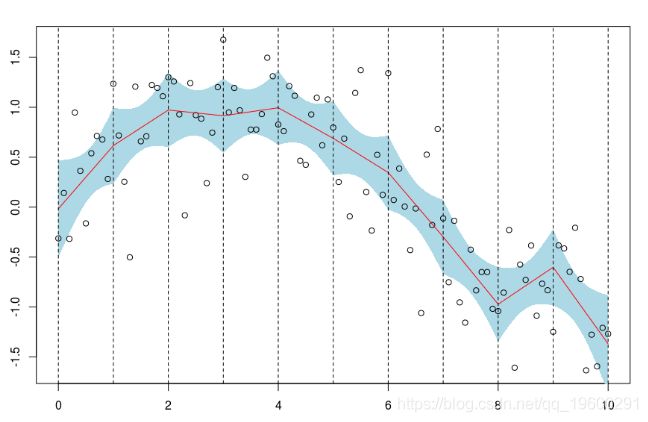
我们可以得到一个置信区间

polygon(c(xr,rev(xr)),c(P[,2],rev(P[,3]))

points(db)

如果我们保持先前选择的两个节点，但考虑泰勒的2阶的展开，我们得到

matplot(xr,B,type="l")
abline(v=c(0,2,5,10),lty=2)

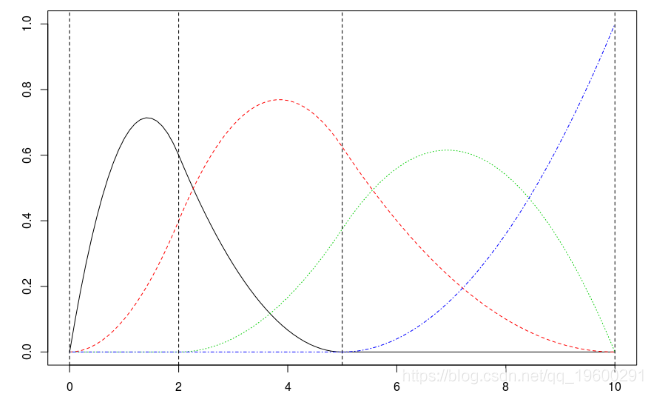
如果我们考虑常数和基于样条的第一部分，我们得到

B=cbind(1,B)
lines(xr,B[,1:k]%*%coefficients(reg)[1:k],col=k-1,lty=k-1)

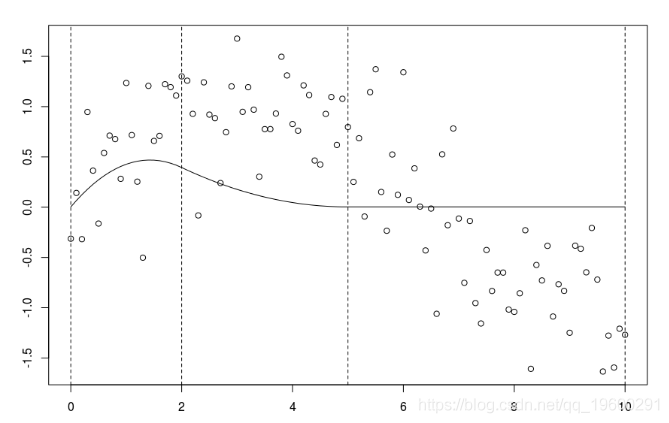
如果我们将常数项，第一项和第二项相加，则我们得到的部分在第一个节点之前位于左侧，

k=3
lines(xr,B[,1:k]%*%coefficients(reg)[1:k]

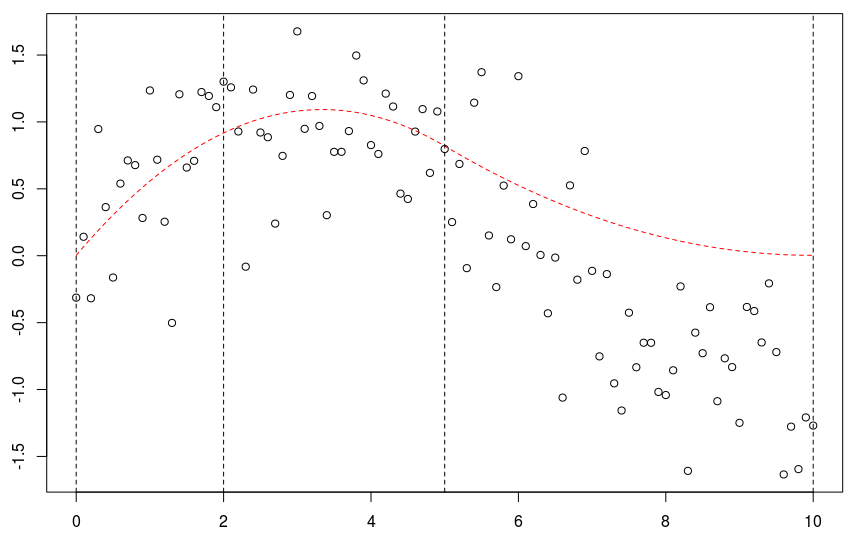
通过基于样条的矩阵中的三个项，我们可以得到两个节点之间的部分，

lines(xr,B[,1:k]%*%coefficients(reg)[1:k]

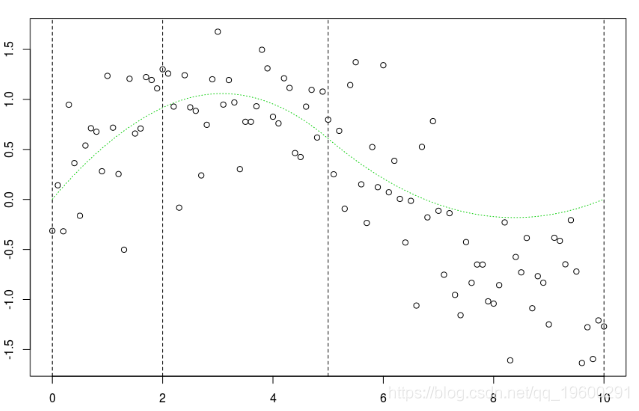
最后，当我们对它们求和时，这次是最后一个节点之后的右侧部分，

k=5

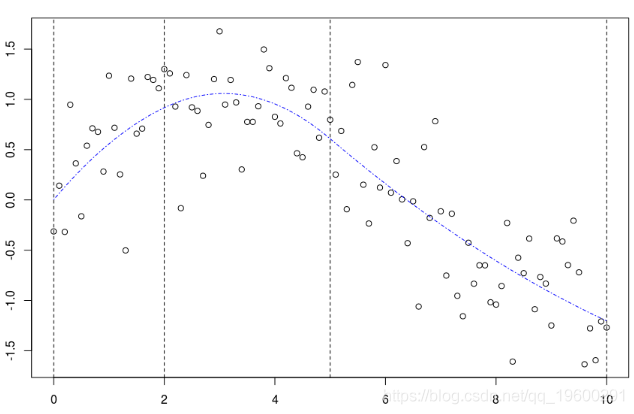
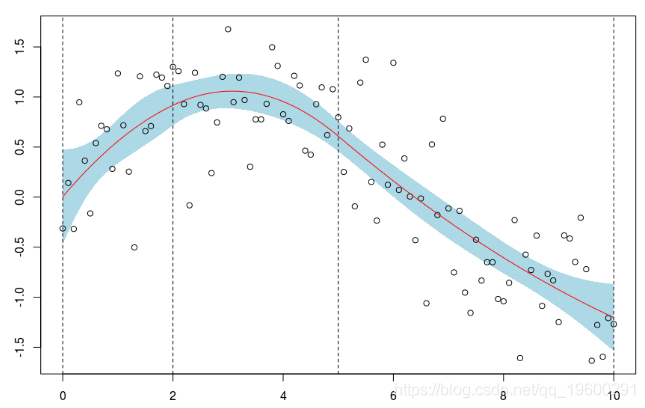
这是我们使用带有两个（固定）节点的二次样条回归得到的结果。可以像以前一样获得置信区间

polygon(c(xr,rev(xr)),c(P[,2],rev(P[,3]))

points(db)
lines(xr,P[,1],col="red")

使用函数 ，可以确保点的连续性 。

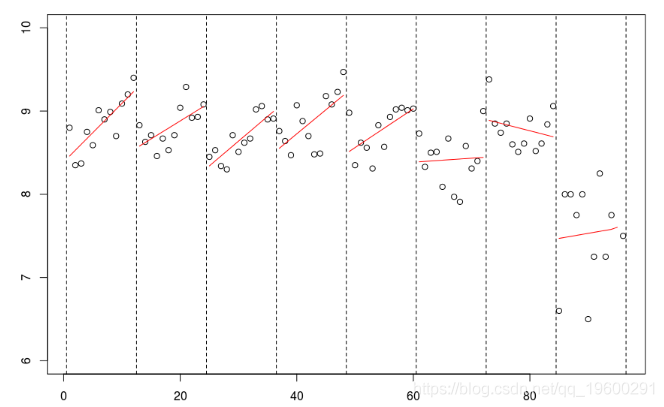
再一次，使用线性样条函数，可以增加连续性约束，

lm(mu~bs(no,knots=c(12*(1:7)+.5),Boundary.knots=c(0,97),

lines(c(1:94,96),predict(reg),col="red")

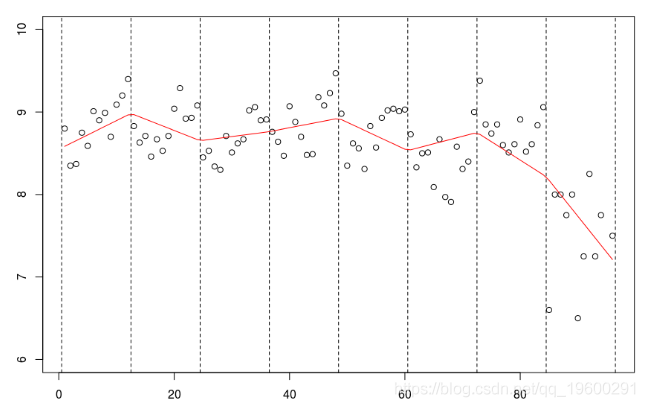
但是我们也可以考虑二次样条，

abline(v=12*(0:8)+.5,lty=2)

lm(mu~bs(no,knots=c(12*(1:7)+.5),Boundary.knots=c(0,97),

---

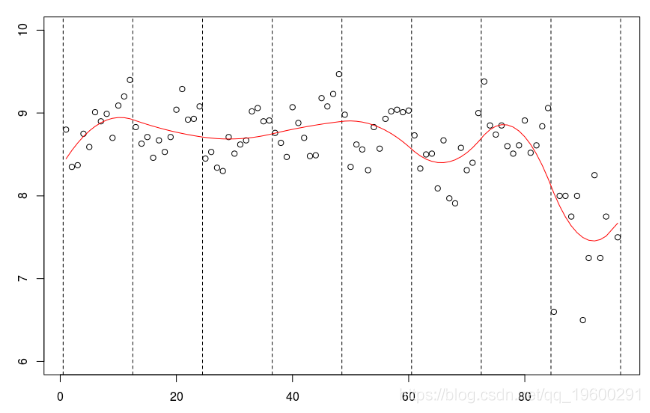
到此这篇关于详解R语言中的多项式回归、局部回归、核平滑和平滑样条回归模型的文章就介绍到这了,更多相关R语言多项式回归、局部回归内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！