Python机器学习应用之基于线性判别模型的分类篇详解

目录

• 一、Introduction
• 1 LDA的优点
• 2 LDA的缺点
• 3 LDA在模式识别领域与自然语言处理领域的区别
• 二、Demo
• 三、基于LDA 手写数字的分类
• 四、小结

一、Introduction

线性判别模型（LDA）在模式识别领域（比如人脸识别等图形图像识别领域）中有非常广泛的应用。LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。 LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。即：将数据投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近方法。

1 LDA的优点

• 在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识；
• LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优

2 LDA的缺点

• LDA不适合对非高斯分布样本进行降维，PCA也有这个问题
• LDA降维最多降到类别数 k-1 的维数，如果我们降维的维度大于 k-1，则不能使用 LDA。当然目前有一些LDA的进化版算法可以绕过这个问题
• LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好
• LDA可能过度拟合数据

3 LDA在模式识别领域与自然语言处理领域的区别

在自然语言处理领域，LDA是隐含狄利克雷分布，它是一种处理文档的主题模型。本文讨论的是线性判别分析 LDA除了可以用于降维以外，还可以用于分类。一个常见的LDA分类基本思想是假设各个类别的样本数据符合高斯分布，这样利用LDA进行投影后，可以利用极大似然估计计算各个类别投影数据的均值和方差，进而得到该类别高斯分布的概率密度函数。当一个新的样本到来后，我们可以将它投影，然后将投影后的样本特征分别带入各个类别的高斯分布概率密度函数，计算它属于这个类别的概率，最大的概率对应的类别即为预测类别

二、Demo

#%%导入基本库
# 基础数组运算库导入
import numpy as np
# 画图库导入
import matplotlib.pyplot as plt
# 导入三维显示工具
from mpl_toolkits.mplot3d import Axes3D
# 导入LDA模型
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 导入demo数据制作方法
from sklearn.datasets import make_classification
#%%模型训练
# 制作四个类别的数据，每个类别100个样本
X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0,
                           n_classes=4, n_informative=2, n_clusters_per_class=1,
                           class_sep=3, random_state=10)
# 将四个类别的数据进行三维显示
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o', c=y)
plt.show()

#%%建立 LDA 模型
lda = LinearDiscriminantAnalysis()
# 进行模型训练
lda.fit(X, y)
#%%查看lda的参数
print(lda.get_params())

#%%数据可视化
#模型预测
X_new = lda.transform(X)
# 可视化预测数据
plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)
plt.show()

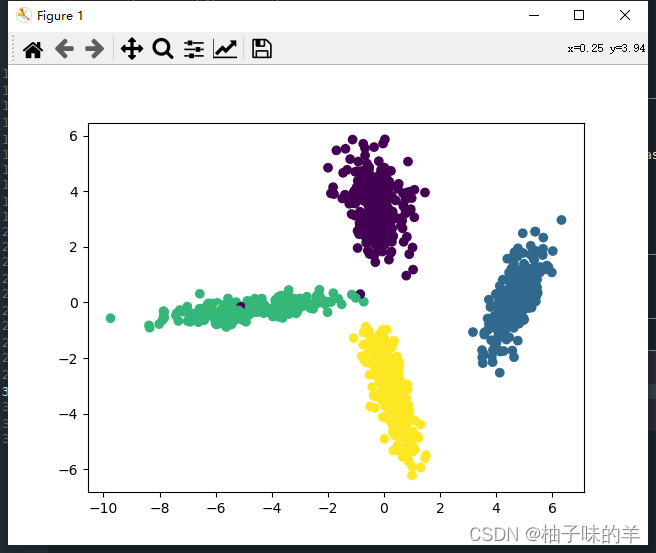
#%%使用新的数据进行测试
a = np.array([[-1, 0.1, 0.1]])
print(f"{a} 类别是: ", lda.predict(a))
print(f"{a} 类别概率分别是: ", lda.predict_proba(a))

a = np.array([[-12, -100, -91]])
print(f"{a} 类别是: ", lda.predict(a))
print(f"{a} 类别概率分别是: ", lda.predict_proba(a))

a = np.array([[-12, -0.1, -0.1]])
print(f"{a} 类别是: ", lda.predict(a))
print(f"{a} 类别概率分别是: ", lda.predict_proba(a))

a = np.array([[0.1, 90.1, 9.1]])
print(f"{a} 类别是: ", lda.predict(a))
print(f"{a} 类别概率分别是: ", lda.predict_proba(a))

三、基于LDA 手写数字的分类

#%%导入库函数
# 导入手写数据集 MNIST
from sklearn.datasets import load_digits
# 导入训练集分割方法
from sklearn.model_selection import train_test_split
# 导入LDA模型
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 导入预测指标计算函数和混淆矩阵计算函数
from sklearn.metrics import classification_report, confusion_matrix
# 导入绘图包
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
#%% 导入MNIST数据集
mnist = load_digits()
# 查看数据集信息
print('The Mnist dataeset:\n',mnist)

# 分割数据为训练集和测试集
x, test_x, y, test_y = train_test_split(mnist.data, mnist.target, test_size=0.1, random_state=2)

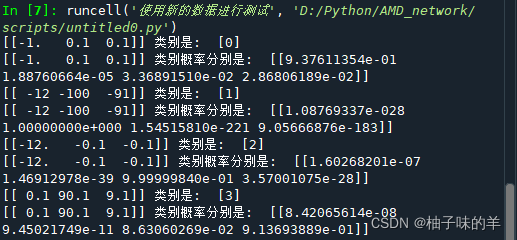
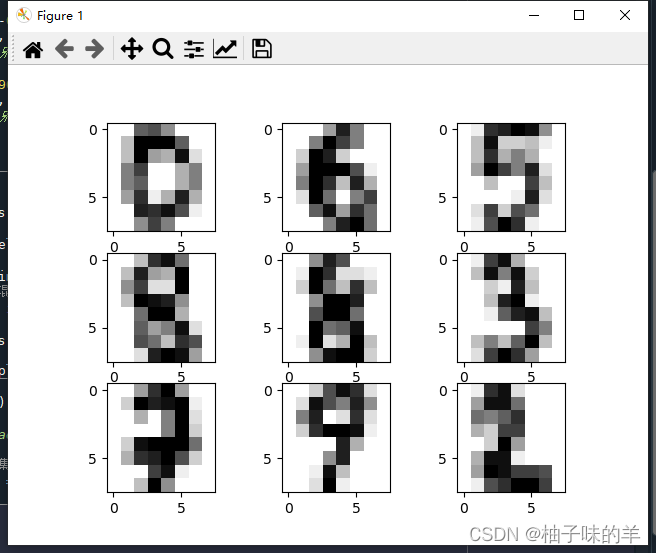
#%%## 输出示例图像
images = range(0,9)

plt.figure(dpi=100)
for i in images:
    plt.subplot(330 + 1 + i)
    plt.imshow(x[i].reshape(8, 8), cmap = matplotlib.cm.binary,interpolation="nearest")
# show the plot
plt.show()

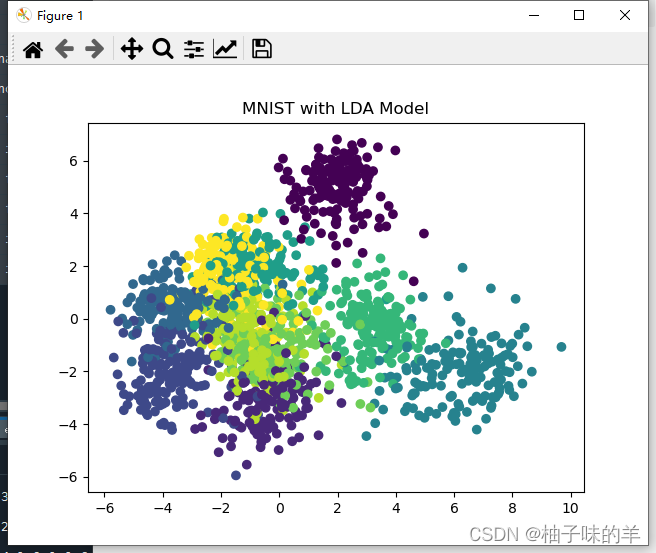
#%%利用LDA对手写数字进行训练与预测
m_lda = LinearDiscriminantAnalysis()# 建立 LDA 模型
# 进行模型训练
m_lda.fit(x, y)
# 进行模型预测
x_new = m_lda.transform(x)
# 可视化预测数据
plt.scatter(x_new[:, 0], x_new[:, 1], marker='o', c=y)
plt.title('MNIST with LDA Model')
plt.show()

#%% 进行测试集数据的类别预测
y_test_pred = m_lda.predict(test_x)
print("测试集的真实标签:\n", test_y)
print("测试集的预测标签:\n", y_test_pred)
#%% 进行预测结果指标统计 统计每一类别的预测准确率、召回率、F1分数
print(classification_report(test_y, y_test_pred))
# 计算混淆矩阵
C2 = confusion_matrix(test_y, y_test_pred)
# 打混淆矩阵
print(C2)

# 将混淆矩阵以热力图的防线显示
sns.set()
f, ax = plt.subplots()
# 画热力图
sns.heatmap(C2, cmap="YlGnBu_r", annot=True, ax=ax)
# 标题
ax.set_title('confusion matrix')
# x轴为预测类别
ax.set_xlabel('predict')
# y轴实际类别
ax.set_ylabel('true')
plt.show()

四、小结

LDA适用于线性可分数据，在非线性数据上要谨慎使用。 886~~~

到此这篇关于Python机器学习应用之基于线性判别模型的分类篇详解的文章就介绍到这了,更多相关Python 线性判别模型的分类内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！