Python实现多项式拟合正弦函数详情

目录
  • 1. 实验目的
  • 2. 实验要求
  • 3. 实验内容
    • 3.1 算法原理

1. 实验目的

掌握最小二乘法求解（无惩罚项的损失函数）、掌握加惩罚项（2 范数）的损失函数优化、梯度下降法、共轭梯度法、理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)

2. 实验要求

生成数据，加入噪声；

用高阶多项式函数拟合曲线；

用解析解求解两种 loss 的最优解（无正则项和有正则项）

优化方法求解最优解（梯度下降，共轭梯度）；

用你得到的实验数据，解释过拟合。

用不同数据量，不同超参数，不同的多项式阶数，比较实验效果。

语言不限，可以用 matlab，python。求解解析解时可以利用现成的矩阵求逆。梯度下降，共轭梯度要求自己求梯度，迭代优化自己写。不许用现成的平台，例如 pytorch，tensorflow 的自动微分工具。

3. 实验内容

3.1 算法原理

本实验需要用多项式来拟合正弦函数。在 m 阶多项式中，有 m+1 个待定系数，m+1 个系数（由低到高）组成的（列）向量记作 w。要确定 w，用最小二乘法。

设 E(w) = 1/2 * (Xw – Y)^T(Xw – Y)，其中，X 为多项式中各个未知项代入观测数据求得的矩阵，若记 Xi 为 X 的第 i 行的向量，则 Xi[j]为第 i 个观测数据 xi 的 j 次方，记有 n 组观测数据，多项式最高次为 m，易知 X 的维度为 n * (m+1)。Y 为观测标签向量。即 Y[j]为第 j 组观测数据的标签值（即 y 值）。从而问题转化为：求向量 w，使得 E(w)最小。

  • 若不加入正则项，令损失函数导数为零，求 w
  • 若加入正则项，令损失函数导数为零，求 w
  • 加入正则项，对损失函数用梯度下降，当损失函数收敛时，求 w
  • 加入正则项，对损失函数用共轭梯度法，循环迭代 m+1 次，求 w 3.2 算法实现 生成数据，加入噪声

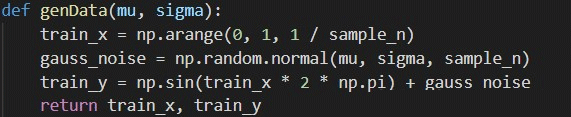
用高阶多项式函数拟合曲线；

用解析解求解两种 loss 的最优解（无正则项和有正则项）

无正则项：

有正则项：

优化方法求解最优解（梯度下降，共轭梯度）

梯度下降法：

共轭梯度法：

用你得到的实验数据，解释过拟合。

多项式次数为 1 时：

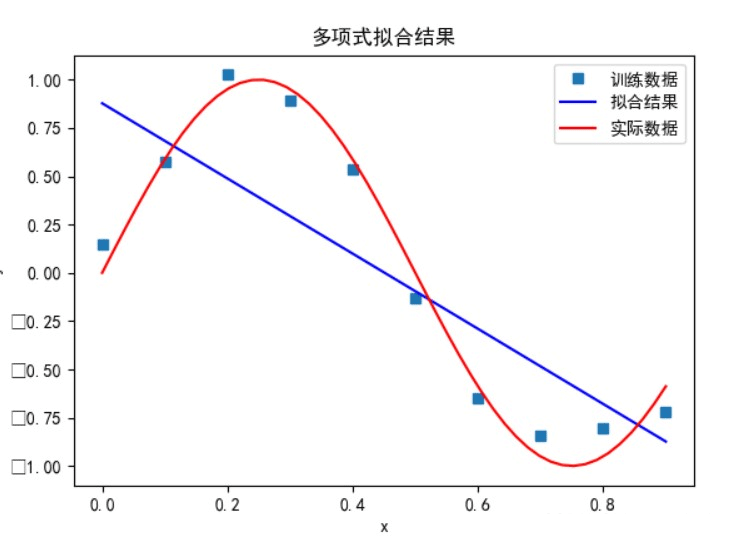
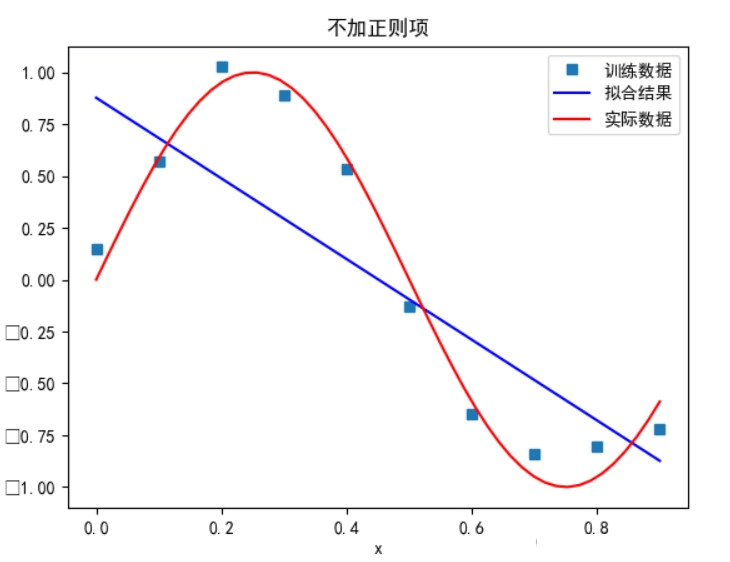
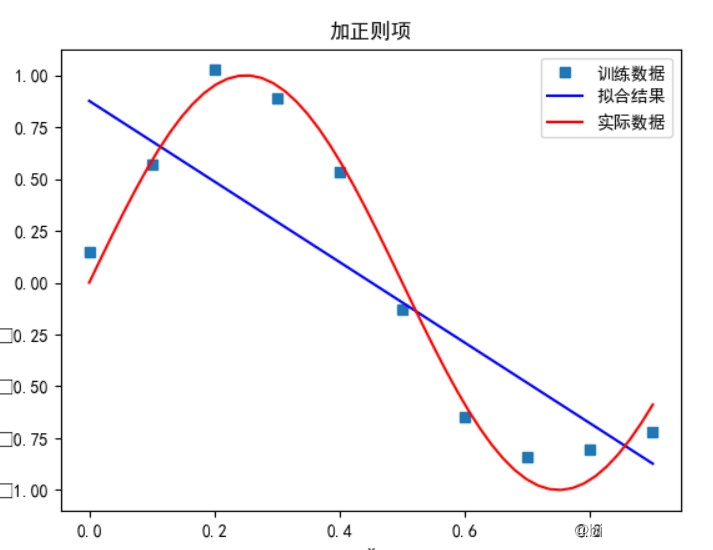
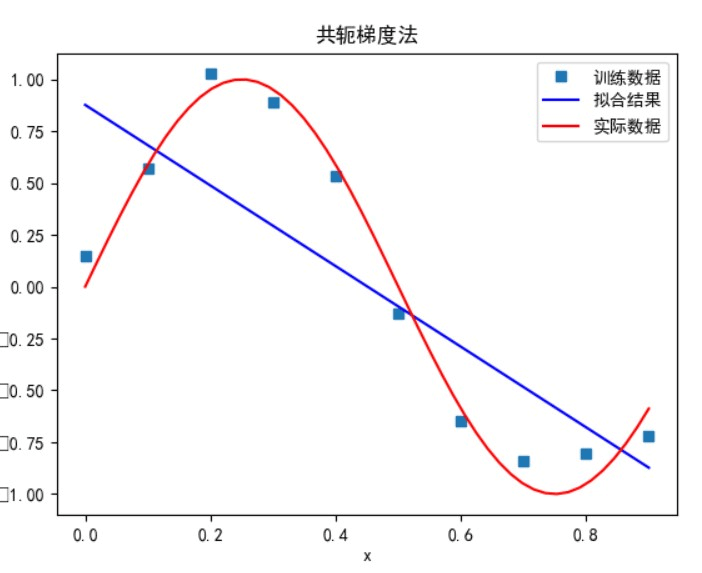
多项式次数为 3 时：

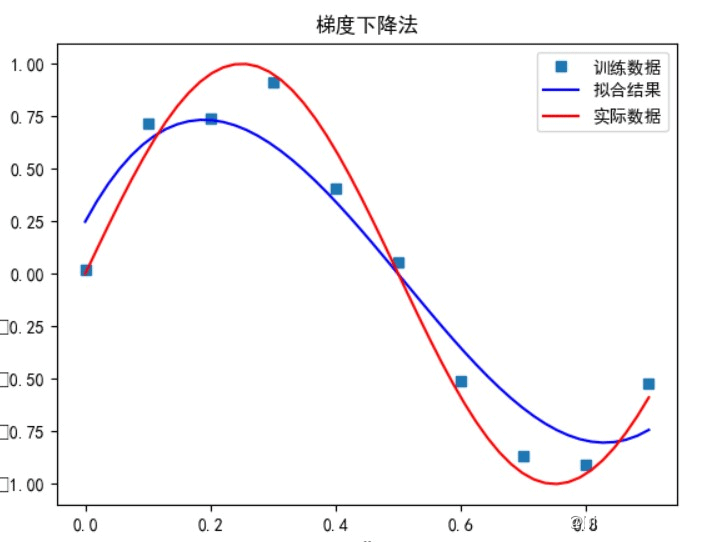
当多项式次数为 5 时：

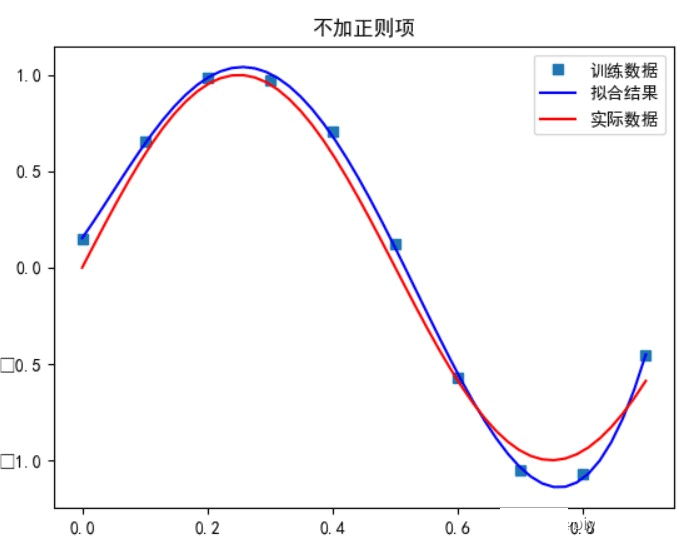
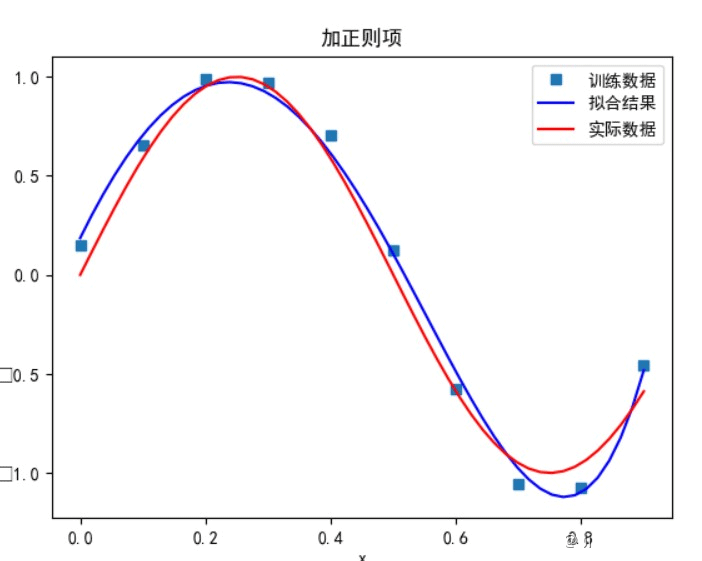
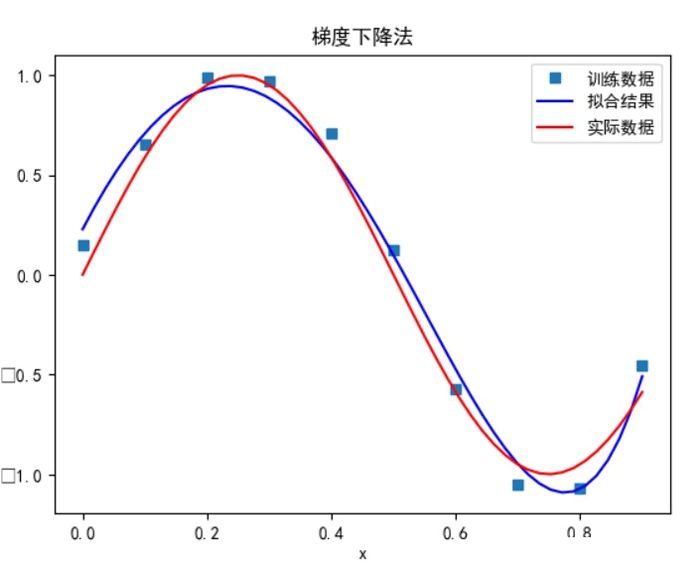
当多项式次数为 7 时：

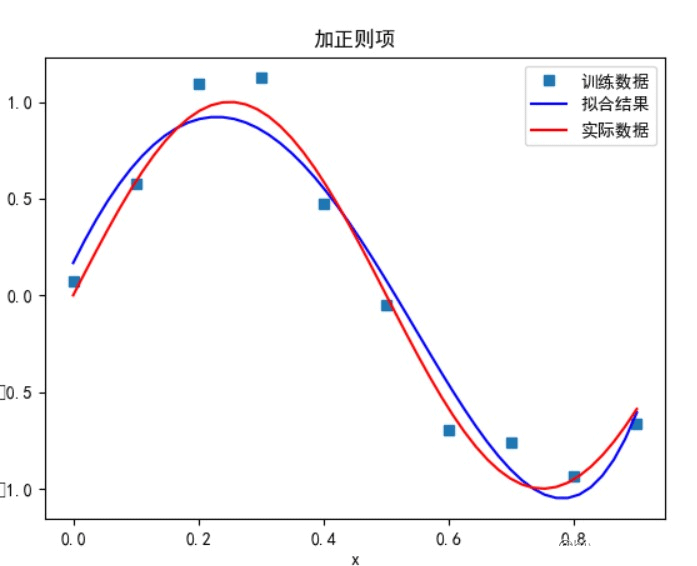
当多项式次数为 9 时：

到此这篇关于Python实现多项式拟合正弦函数详情的文章就介绍到这了,更多相关Python拟合正弦函数内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • python 图像处理画一个正弦函数代码实例

    python 图像处理画一个正弦函数代码实例

    这篇文章主要介绍了python 图像处理画一个正弦函数代码实例,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下 import numpy as np from PIL import Image import matplotlib.pyplot as plt import math size = 300 new_im = Image.new("RGBA",(size,size)) #创建一个空的图片 a_img = np.array(ne

  • Python实现多项式拟合正弦函数详情

    Python实现多项式拟合正弦函数详情

    目录 1. 实验目的 2. 实验要求 3. 实验内容 3.1 算法原理 1. 实验目的 掌握最小二乘法求解(无惩罚项的损失函数).掌握加惩罚项(2 范数)的损失函数优化.梯度下降法.共轭梯度法.理解过拟合.克服过拟合的方法(如加惩罚项.增加样本) 2. 实验要求 生成数据,加入噪声: 用高阶多项式函数拟合曲线: 用解析解求解两种 loss 的最优解(无正则项和有正则项) 优化方法求解最优解(梯度下降,共轭梯度): 用你得到的实验数据,解释过拟合. 用不同数据量,不同超参数,不同的多项式阶数,比较

  • Python 确定多项式拟合/回归的阶数实例

    通过 1至10 阶来拟合对比 均方误差及R评分,可以确定最优的"最大阶数". import numpy as np import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression,Perceptron from sklearn.metrics import mean_squared_

  • Python实现的多项式拟合功能示例【基于matplotlib】

    Python实现的多项式拟合功能示例【基于matplotlib】

    本文实例讲述了Python实现的多项式拟合功能.分享给大家供大家参考,具体如下: # -*- coding: utf-8 -*- #! python2 import numpy as np import matplotlib.pyplot as plt from pylab import mpl mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体 plt.rcParams['axes.unicode_minus']=False #解决负数坐

  • Python 普通最小二乘法(OLS)进行多项式拟合的方法

    多元函数拟合.如 电视机和收音机价格多销售额的影响,此时自变量有两个. python 解法: import numpy as np import pandas as pd #import statsmodels.api as sm #方法一 import statsmodels.formula.api as smf #方法二 import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D df = pd.read_c

  • 在python中利用numpy求解多项式以及多项式拟合的方法

    构建一个二阶多项式:x^2 - 4x + 3 多项式求解 >>> p = np.poly1d([1,-4,3]) #二阶多项式系数 >>> p(0) #自变量为0时多项式的值 3 >>> p.roots #多项式的根 array([3., 1.]) >>> p(p.roots) #多项式根处的值 array([0., 0.]) >>> p.order #多项式的阶数 2 >>> p.coeffs #

  • python多项式拟合之np.polyfit 和 np.polyld详解

    python数据拟合主要可采用numpy库,库的安装可直接用pip install numpy等. 1. 原始数据:假如要拟合的数据yyy来自sin函数,np.sin import numpy as np import matplotlib.pyplot as plt xxx = np.arange(0, 1000) # x值,此时表示弧度 yyy = np.sin(xxx*np.pi/180) #函数值,转化成度 2. 测试不同阶的多项式,例如7阶多项式拟合,使用np.polyfit拟合,np

  • 利用python做数据拟合详情

    利用python做数据拟合详情

    目录 1.例子:拟合一种函数Func,此处为一个指数函数. 2. 例子:拟合一个Gaussian函数 3. 用一个lmfit的包来实现2中的Gaussian函数拟合 1.例子:拟合一种函数Func,此处为一个指数函数. 出处: SciPy v1.1.0 Reference Guide #Header import numpy as np import matplotlib.pyplot as plt from scipy.optimize import curve_fit #Define a f

  • Python实现的拟合二元一次函数功能示例【基于scipy模块】

    Python实现的拟合二元一次函数功能示例【基于scipy模块】

    本文实例讲述了Python实现的拟合二元一次函数功能.分享给大家供大家参考,具体如下: 背景: 使用scipy拟合一元二次函数. 参考: HYRY Studio-<用Python做科学计算> 代码: # -*- coding:utf-8 -*- #! python3 import numpy as np from scipy.optimize import leastsq import pylab as pl def func(x,p): """ 数组拟合函数 &

  • python数据分析之时间序列分析详情

    python数据分析之时间序列分析详情

    目录 前言 时间序列的相关检验 白噪声检验 平稳性检验 自相关和偏相关分析 移动平均算法 简单移动平均法 简单指数平滑法 霍尔特(Holt)线性趋势法 Holt-Winters季节性预测模型 ARIMA模型 ARMA模型 针对ARMA模型自动选择合适的参数 时序数据的异常值检测 前言 时间序列分析是基于随机过程理论和数理统计学方法: 每日的平均气温 每天的销售额 每月的降水量 时间序列分析主要通过statsmodel库的tsa模块完成: 根据时间序列的散点图,自相关函数和偏自相关函数图识别序列是

  • python实现三维拟合的方法

    如下所示: from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) #列出实验数据 point=[[2,3,48],[4,5,50],[5,7,51],[8,9,55],[9,12,56]] plt.xlabel("X1") plt.ylabel("X2") #

随机推荐