C++关于树的定义全面梳理

目录
  • 概念
    • 树
    • 树的叶子节点
    • 节点的度
    • 分支结点
    • 树的度
    • 树的高度
    • 树的深度
    • 二叉树
    • 二叉树的特点
    • 满二叉树
    • 完全二叉树
    • 二叉查找树
  • 示例
    • 代码实现
      • 开发环境
      • 运行结果

概念

本文以一个简单的树为例，如下图，来记录树的一些概念。

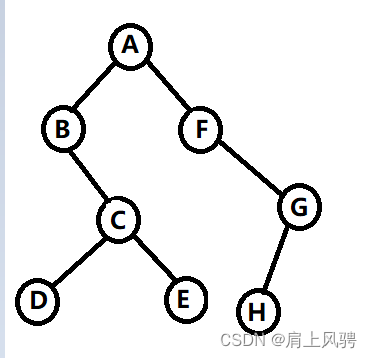
树

一种由n个节点组成的具有一定层次关系的有限数据集合。每个节点有0个或者n个子节点，有一个根节点（没有前驱只有后继），除根节点外每一个节点都有一个前驱，0个或多个后继。

树的叶子节点

只有一个前驱，没有后继的节点，为最外层的节点。叶子节点的度为0。

节点的度

节点拥有的子树的数目。

分支结点

度不为0的结点。

树的度

树中结点的最大的度。

树的高度

任意叶子节点距离根节点的最大深度。此文中树的叶子节点为D、E、H，距离根节点的深度都为4，故高度为4。

树的深度

即从根节点到叶子节点的行数。此文中树的深度为4。

二叉树

二叉树是每个节点最多有两个子树的树结构。

它有五种基本形态：

二叉树可以是空集；

根可以有空的左子树或右子树；

或者左、右子树皆为空。

二叉树的特点

二叉树第i层上的结点数目最多为2i-1(i>=1)

深度为k的二叉树至多有2k-1个结点（k>=1）

包含n个结点的二叉树的高度至少为(log2n)+1

满二叉树

高度为h，并且由2h-1个节点组成的二叉树。

完全二叉树

一棵二叉树中，只有最下面两层节点的度可以小于2，并且最下层的叶节点集中在靠左的若干位置上，这样的二叉树称为完全二叉树。

二叉查找树

二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点，x结点包含关键字key，结点x的key值计为key[x]。如果y是x的左子树中的一个结点，则key[y]<=key[x]；如果y是x的右子树的一个结点，则key[y]>=key[x]。

特点：

1.若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。

2.任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

3.任意结点的左、右子树也分别为二叉查找树。

4.没有键值相等的结点。

示例

下面直接上代码，一个简单的树的创建、遍历输出，叶子节点数，高度。

代码实现

Tree.h

#pragma once
typedef struct MYTREE {
	char data;
	struct MYTREE* lChild;
	struct MYTREE* rChild;
}MyTree;
class Tree
{
public:
	Tree();
	~Tree();
	void CreateTree();
	void TraverseTree(MyTree *root);
	void GetLeafNode(MyTree *root,int &num);
	int GetTreeDepth(MyTree *root);
	void GetTreeNode(MyTree *root, int &num);
};

Tree.cpp

#include "Tree.h"
#include <iostream>
#include<algorithm>//max,min
using namespace std;
Tree::Tree()
{
}
Tree::~Tree()
{
}
void Tree::CreateTree()
{
	MyTree t1 = {'A',nullptr,nullptr};
	MyTree t2 = { 'B',nullptr,nullptr };
	MyTree t3 = { 'C',nullptr,nullptr };
	MyTree t4 = { 'D',nullptr,nullptr };
	MyTree t5 = { 'E',nullptr,nullptr };
	MyTree t6 = { 'F',nullptr,nullptr };
	MyTree t7 = { 'G',nullptr,nullptr };
	MyTree t8 = { 'H',nullptr,nullptr };
	t1.lChild = &t2;
	t1.rChild = &t6;
	t2.rChild = &t3;
	t3.lChild = &t4;
	t3.rChild = &t5;
	t6.rChild = &t7;
	t7.lChild = &t8;
	TraverseTree(&t1);
	cout << endl;
	int leafNum = 0;
	GetLeafNode(&t1,leafNum);
	cout << "leaf num: " << leafNum << endl;
	int treeDepth = GetTreeDepth(&t1);
	cout << "depth:" << treeDepth << endl;
	int nodeNum = 0;
	GetTreeNode(&t1,nodeNum);
	cout << "node num; " << nodeNum << endl;
}
void Tree::TraverseTree(MyTree *root)
{
	if (root == nullptr)
	{
		return;
	}
	TraverseTree(root->lChild);
	cout << root->data;
	TraverseTree(root->rChild);
}
void Tree::GetLeafNode(MyTree *root,int &num)
{
	if (root == nullptr)
	{
		return ;
	}
	if (root->lChild == nullptr && root->rChild == nullptr)
	{
		num++;
	}
	GetLeafNode(root->lChild,num);
	GetLeafNode(root->rChild,num);
}
int Tree::GetTreeDepth(MyTree * root)
{
	int num = 0;
	if (root == nullptr)
	{
		return num;
	}
	int lNum = GetTreeDepth(root->lChild);
	int rNum = GetTreeDepth(root->rChild);
	return max(lNum,rNum)+1;
}
void Tree::GetTreeNode(MyTree * root, int & num)
{
	if (root == nullptr)
	{
		return;
	}
	++num;
	GetTreeNode(root->lChild,num);
	GetTreeNode(root->rChild,num);
}

main.cpp

#include <iostream>
#include "Tree.h"
using namespace std;
void test() {
	Tree t;
	t.CreateTree();
}
int main()
{
	test();
	return 0;
}

开发环境

vs2017控制台输出程序。

运行结果

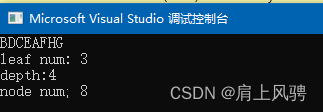
到此这篇关于C++关于树的定义全面梳理的文章就介绍到这了,更多相关C++树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • C++数据结构之AVL树的实现

    C++数据结构之AVL树的实现

    目录 1.概念 (1)二叉搜索树的缺点 (2)定义节点 2.插入 (1)拆分 (2)找节点与插节点 (3)更新平衡因子与旋转 3.判断 4.完整代码及测试代码 完整代码 测试代码 1.概念 (1)二叉搜索树的缺点 要手撕AVL树,我们首先要知道什么是AVL树.AVL树是在二叉搜索树的基础之上改造的.当我们插入的是一个有序的序列的时候,二叉搜素树会使用一条直线来进行存储,这样并不利于查找. 当遇到这种情况的时候我们就需要对这棵树来进行调整.AVL树会通过旋转等操作,来规避这种情况.最终满足每一个节

  • C++详细实现红黑树流程详解

    C++详细实现红黑树流程详解

    目录 红黑树的概念 红黑树的性质 红黑树的定义与树结构 插入 新增结点插入后维护红黑树性质的主逻辑 旋转 验证 红黑树与AVl树的比较 红黑树的应用 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black. 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的 概念总结: 红黑树是二叉搜索树的升级,结点里面存放的成员col标记当前结点的颜色,它的最长路径最多是最短路径的二倍,红黑

  • C++深入讲解哈夫曼树

    C++深入讲解哈夫曼树

    目录 哈夫曼树的基本概念 1)路径 2)路径长度 3)权 4)结点的带权路径长度 5)树的带权路径长度 6)哈夫曼树 哈夫曼树的构造算法 哈夫曼树的构造过程 哈夫曼树算法的实现 1)结点的存储结构 2)构建哈夫曼树 哈夫曼树的基本概念 Q:什么是哈夫曼树 A:哈夫曼树又称最优树,是一类带权路径长度最短的树.在正式了解哈夫曼树之前,我们需要了解一些概念. 1)路径 Q:什么是路径 A:从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径. 2)路径长度 Q:什么是路径长度 A:路径上的分支

  • C++深入细致探究二叉搜索树

    C++深入细致探究二叉搜索树

    目录 1.二叉搜索树的概念 2.二叉搜索树的操作 二叉搜索树的查找 二叉搜索树的插入 二叉搜索树的删除 3.二叉搜索树的实现 4.二叉搜索树的性能分析 1.二叉搜索树的概念  二叉搜索树又称二叉排序树,它可以是一颗空树,亦可以是一颗具有如下性质的二叉树:   ①若根节点的左子树不为空,则左子树上的所有节点的值域都小于根节点的值   ②若根节点的右子树不为空,则右子树上的所有节点的值域都大于根节点的值   ③根节点的左右子树分别也是一颗二叉搜索树 例如下面的这棵二叉树就是一棵二叉搜索树: 注意:判

  • C++链式二叉树深入分析

    C++链式二叉树深入分析

    目录 二叉树的结构和概念 二叉树的操作 前序遍历 中序遍历和后序遍历 二叉树的节点个数 求二叉树叶子结点个数 求二叉树的深度 在二叉树查找为X的结点 之前我们的重点学习二叉树都是完全二叉树,接下来我们来说下普通二叉树,普通的二叉树如果我们使用数组存储,那么会浪费相当多的空间的,所以我们选择链表存储,我们先再来复习下二叉树的结构吧. 二叉树的结构和概念 二叉树概念是: 1. 空树 2. 非空:根节点,根节点的左子树.根节点的右子树组成的. 从概念中可以看出,二叉树定义是递归式的. 我们就手动创建一

  • C++超详细讲解树与二叉树

    C++超详细讲解树与二叉树

    目录 树 树的定义 树的名词解释 树的表示 树的存储结构 二叉树的概念及结构 二叉树的概念 二叉树的性质 二叉树的存储结构 顺序存储结构 链式存储结构 树 树的定义 Q:什么是树 A:树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合.把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的. Q:树有什么特点 有一个特殊的结点,称为根结点,根节点没有前驱结点. 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1.T2.…….T

  • C++简单又轻松建立链式二叉树流程

    C++简单又轻松建立链式二叉树流程

    目录 递归建立二叉树 二叉树的结构体 二叉树初始化 先序遍历 中序遍历 后序遍历 具体例题 输入的格式 全部源码 总结 递归建立二叉树 二叉树的结构体 typedef struct Node { int data; Node* lchild; Node* rchild; }BiNode,*BiTree; 二叉树顾名思义最多只有两个子结点和一个数据域,既然是链式那么子结点定义为结点指针类型,数据域就可以根据需要设置了,可以是整型也可以是字符型. 二叉树初始化 BiTree createBiTree

  • C++超详细实现二叉树的遍历

    C++超详细实现二叉树的遍历

    目录 二叉树的遍历 前序遍历 中序遍历 后序遍历 层序遍历 二叉树的遍历 Q:什么是二叉树的遍历? A:二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次,且仅被访问一次. Q:二叉树有几种遍历方法? A:二叉树的遍历方法可以有很多种,如果限制了从左到右的习惯方式,那么主要分为以下四种:先序遍历,中序遍历,后序遍历,层序遍历. 前序遍历 Q:什么是先序遍历 A:先序遍历就是先访问树的根节点,再访问树的左子节点,再访问右子节点.可以想象为,从一棵二叉树根节点

  • C++使用数组来实现哈夫曼树

    C++使用数组来实现哈夫曼树

    目录 写在前面 构造思想 算法设计 构造实例 理解代码 确定结构体 循环找出最小值 调用细节 调试试图 总结 写在前面 哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树.所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数).树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶

  • C++关于树的定义全面梳理

    C++关于树的定义全面梳理

    目录 概念 树 树的叶子节点 节点的度 分支结点 树的度 树的高度 树的深度 二叉树 二叉树的特点 满二叉树 完全二叉树 二叉查找树 示例 代码实现 开发环境 运行结果 概念 本文以一个简单的树为例,如下图,来记录树的一些概念. 树 一种由n个节点组成的具有一定层次关系的有限数据集合.每个节点有0个或者n个子节点,有一个根节点(没有前驱只有后继),除根节点外每一个节点都有一个前驱,0个或多个后继. 树的叶子节点 只有一个前驱,没有后继的节点,为最外层的节点.叶子节点的度为0. 节点的度 节点拥有

  • C++ AVL树插入新节点后的四种调整情况梳理介绍

    C++ AVL树插入新节点后的四种调整情况梳理介绍

    AVL树是一个高度平衡的二叉搜索树 满足二叉搜索树的所有特性. 左子树和右子树的高度之差的绝对值不大于1. 此处AVL树结点的定义 template<class K, class V> struct AVLTreeNode { AVLTreeNode<K, V> _left; AVLTreeNode<K, V> _right; AVLTreeNode<K, V> _parent; pair<K, V> _kv; int _bf; //平衡因子 A

  • python数据结构树和二叉树简介

    一.树的定义 树形结构是一类重要的非线性结构.树形结构是结点之间有分支,并具有层次关系的结构.它非常类似于自然界中的树.树的递归定义:树(Tree)是n(n≥0)个结点的有限集T,T为空时称为空树,否则它满足如下两个条件:(1)有且仅有一个特定的称为根(Root)的结点:(2)其余的结点可分为m(m≥0)个互不相交的子集Tl,T2,-,Tm,其中每个子集本身又是一棵树,并称其为根的子树(Subree). 二.二叉树的定义 二叉树是由n(n≥0)个结点组成的有限集合.每个结点最多有两个子树的有序树

  • c语言B树深入理解

    c语言B树深入理解

    B树是为磁盘或其他直接存储设备设计的一种平衡查找树.如下图所示.每一个结点箭头指向的我们称为入度,指出去的称为出度.树结构的结点入度都是1,不然就变成图了,所以我们一般说树的度就是指树结点的出度,也就是一个结点的子结点个数.有了度的概念我们就简单定义一下B树(假设一棵树的最小度数为M):1.每个结点至少有M-1个关键码,至多有2M-1个关键码:2.除根结点和叶子结点外,每个结点至少有M个子结点,至多有2M个子结点:3.根结点至少有2个子结点,唯一例外是只有根结点的情况,此时没有子结点:4.所有叶

  • c语言 树的基础知识(必看篇)

    c语言 树的基础知识(必看篇)

    第一.树的定义: 1.有且只有一个称为根的节点 2.有若干个互不相交的子树,这些子树本身也是一颗树 第二.专业术语: 树的深度:从根节点到最低层,节点的层数 ,称之为树的深度.  根节点是第一层 结点的层次:根节点为第一层,根节点的子节点为第2层,以此类推 叶子节点:没有子节点的节点 非终端节点:实际就是非叶子节点 结点度: 子节点的个数称为度树的度 第三.树的分类 一般树:任意一个节点的子节点的个数不受限制 二叉树:任意一个节点的子节点最多2个,且子节点的位置不可更改 满二叉树:在不增加层数的

  • Trie树(字典树)的介绍及Java实现

    Trie树(字典树)的介绍及Java实现

    简介 Trie树,又称为前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串.与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定.一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串. 它的主要特点如下: 根节点不包含字符,除根节点外的每一个节点都只包含一个字符. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串. 每个节点的所有子节点包含的字符都不相同. 如下是一棵典型的Trie树: Trie的来源是Retrie

  • java数据结构之树基本概念解析及代码示例

    java数据结构之树基本概念解析及代码示例

    Java中树的存储结构实现 一.树 树与线性表.栈.队列等线性结构不同,树是一...节点与节点之间的父子关系,可以为每个节点增加一个parent域,用以记录该节点的父点 树是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合.它是由n(n>0)个有限节点组成一个具有层次关系的集合.把 它叫做"树"是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的. 树定义和基本术语 定义 树(Tree)是n(n≥0)个结点的有限集T,并且当

  • python中树与树的表示知识点总结

    一.什么是树 客观世界中许多事物存在层次关系 人类社会家谱社会组织结构图书信息管理 其中,人类社会家谱如下图所示: 通过上述所说的分层次组织,能够使我们在数据的管理上有更高的效率!那么,对于数据管理的基本操作--查找,我们如何实现有效率的查找呢? 二.查找 查找:根据某个给定关键字K,从集合R中找出关键字与K相同的记录 静态查找:集合中记录是固定的,即对集合的操作没有插入和删除,只有查找 动态查找:集合中记录是动态变化的,即对集合的操作既有查找,还可能发生插入和删除(动态查找不在我们考虑范围内)

  • Java数据结构之链表、栈、队列、树的实现方法示例

    本文实例讲述了Java数据结构之链表.栈.队列.树的实现方法.分享给大家供大家参考,具体如下: 最近无意中翻到一本书,闲来无事写几行代码,实现几种常用的数据结构,以备后查. 一.线性表(链表) 1.节点定义 /**链表节点定义 * @author colonel * */ class Node { public int data; Node next=null; public Node(int data){ this.data=data; } } 2.链表操作类 /**链表操作类 * @auth

  • MySQL用B+树作为索引结构有什么好处

    MySQL用B+树作为索引结构有什么好处

    前言 在MySQL中,无论是Innodb还是MyIsam,都使用了B+树作索引结构(这里不考虑hash等其他索引).本文将从最普通的二叉查找树开始,逐步说明各种树解决的问题以及面临的新问题,从而说明MySQL为什么选择B+树作为索引结构. 一.二叉查找树(BST):不平衡 二叉查找树(BST,Binary Search Tree),也叫二叉排序树,在二叉树的基础上需要满足:任意节点的左子树上所有节点值不大于根节点的值,任意节点的右子树上所有节点值不小于根节点的值.如下是一颗BST: 当需要快速查

随机推荐